|
Band Diagram
In solid-state physics of semiconductors, a band diagram is a diagram plotting various key electron energy levels (Fermi level and nearby energy band edges) as a function of some spatial dimension, which is often denoted ''x''. These diagrams help to explain the operation of many kinds of semiconductor devices and to visualize how bands change with position (band bending). The bands may be coloured to distinguish level filling. A band diagram should not be confused with a band structure plot. In both a band diagram and a band structure plot, the vertical axis corresponds to the energy of an electron. The difference is that in a band structure plot the horizontal axis represents the wave vector of an electron in an infinitely large, homogeneous material (a crystal or vacuum), whereas in a band diagram the horizontal axis represents position in space, usually passing through multiple materials. Because a band diagram shows the ''changes'' in the band structure from place to pl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
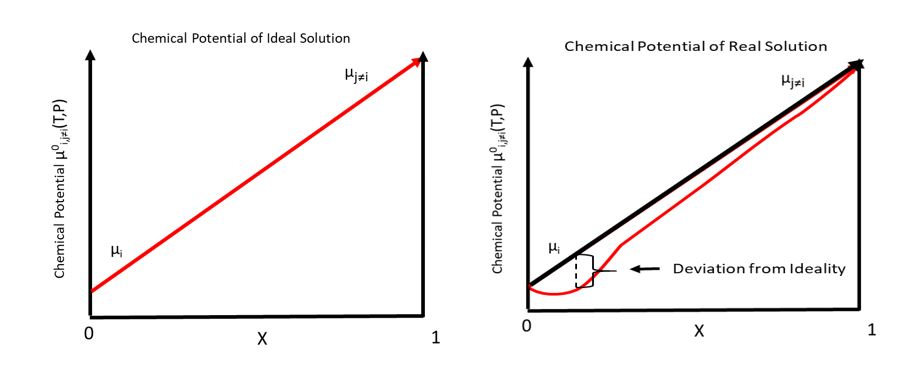
Total Chemical Potential
In thermodynamics, the chemical potential of a species is the energy that can be absorbed or released due to a change of the particle number of the given species, e.g. in a chemical reaction or phase transition. The chemical potential of a species in a mixture is defined as the rate of change of free energy of a thermodynamic system with respect to the change in the number of atoms or molecules of the species that are added to the system. Thus, it is the partial derivative of the free energy with respect to the amount of the species, all other species' concentrations in the mixture remaining constant. When both temperature and pressure are held constant, and the number of particles is expressed in moles, the chemical potential is the partial molar Gibbs free energy. At chemical equilibrium or in phase equilibrium, the total sum of the product of chemical potentials and stoichiometric coefficients is zero, as the free energy is at a minimum. In a system in diffusion equilibrium, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heterojunction
A heterojunction is an interface between two layers or regions of dissimilar semiconductors. These semiconducting materials have unequal band gaps as opposed to a homojunction. It is often advantageous to engineer the electronic energy bands in many solid-state device applications, including semiconductor lasers, solar cells and transistors. The combination of multiple heterojunctions together in a device is called a heterostructure, although the two terms are commonly used interchangeably. The requirement that each material be a semiconductor with unequal band gaps is somewhat loose, especially on small length scales, where electronic properties depend on spatial properties. A more modern definition of heterojunction is the interface between any two solid-state materials, including crystalline and amorphous structures of metallic, insulating, fast ion conductor and semiconducting materials. Manufacture and applications Heterojunction manufacturing generally requires the use of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Poisson's Equation
Poisson's equation is an elliptic partial differential equation of broad utility in theoretical physics. For example, the solution to Poisson's equation is the potential field caused by a given electric charge or mass density distribution; with the potential field known, one can then calculate electrostatic or gravitational (force) field. It is a generalization of Laplace's equation, which is also frequently seen in physics. The equation is named after French mathematician and physicist Siméon Denis Poisson. Statement of the equation Poisson's equation is \Delta\varphi = f where \Delta is the Laplace operator, and f and \varphi are real or complex-valued functions on a manifold. Usually, f is given and \varphi is sought. When the manifold is Euclidean space, the Laplace operator is often denoted as and so Poisson's equation is frequently written as \nabla^2 \varphi = f. In three-dimensional Cartesian coordinates, it takes the form \left( \frac + \frac + \frac \right)\va ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Space Charge
Space charge is an interpretation of a collection of electric charges in which excess electric charge is treated as a continuum of charge distributed over a region of space (either a volume or an area) rather than distinct point-like charges. This model typically applies when charge carriers have been emitted from some region of a solid—the cloud of emitted carriers can form a space charge region if they are sufficiently spread out, or the charged atoms or molecules left behind in the solid can form a space charge region. Space charge only occurs in dielectric media (including vacuum) because in a conductive medium the charge tends to be rapidly neutralized or screened. The sign of the space charge can be either negative or positive. This situation is perhaps most familiar in the area near a metal object when it is heated to incandescence in a vacuum. This effect was first observed by Thomas Edison in light bulb filaments, where it is sometimes called the Edison effect. Space ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Energy State
A quantum mechanical system or particle that is bound—that is, confined spatially—can only take on certain discrete values of energy, called energy levels. This contrasts with classical particles, which can have any amount of energy. The term is commonly used for the energy levels of the electrons in atoms, ions, or molecules, which are bound by the electric field of the nucleus, but can also refer to energy levels of nuclei or vibrational or rotational energy levels in molecules. The energy spectrum of a system with such discrete energy levels is said to be quantized. In chemistry and atomic physics, an electron shell, or principal energy level, may be thought of as the orbit of one or more electrons around an atom's nucleus. The closest shell to the nucleus is called the " shell" (also called "K shell"), followed by the " shell" (or "L shell"), then the " shell" (or "M shell"), and so on farther and farther from the nucleus. The shells correspond with the pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anderson's Rule
Anderson's rule is used for the construction of energy band diagrams of the heterojunction between two semiconductor materials. Anderson's rule states that when constructing an energy band diagram, the vacuum levels of the two semiconductors on either side of the heterojunction should be aligned (at the same energy). It is also referred to as the electron affinity rule, and is closely related to the Schottky–Mott rule for metal–semiconductor junctions. Anderson's rule was first described by R. L. Anderson in 1960. Constructing energy band diagrams Once the vacuum levels are aligned it is possible to use the electron affinity and band gap values for each semiconductor to calculate the conduction band and valence band offsets. The electron affinity (usually given by the symbol \chi in solid state physics) gives the energy difference between the lower edge of the conduction band and the vacuum level of the semiconductor. The band gap (usually given the symbol E_) gives t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electron Affinity
The electron affinity (''E''ea) of an atom or molecule is defined as the amount of energy released when an electron attaches to a neutral atom or molecule in the gaseous state to form an anion. ::X(g) + e− → X−(g) + energy Note that this is not the same as the enthalpy change of electron capture ionization, which is defined as negative when energy is released. In other words, the enthalpy change and the electron affinity differ by a negative sign. In solid state physics, the electron affinity for a surface is defined somewhat differently ( see below). Measurement and use of electron affinity This property is used to measure atoms and molecules in the gaseous state only, since in a solid or liquid state their energy levels would be changed by contact with other atoms or molecules. A list of the electron affinities was used by Robert S. Mulliken to develop an electronegativity scale for atoms, equal to the average of the electrons affinity and ionization potential. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Work Function
In solid-state physics, the work function (sometimes spelt workfunction) is the minimum thermodynamic work (i.e., energy) needed to remove an electron from a solid to a point in the vacuum immediately outside the solid surface. Here "immediately" means that the final electron position is far from the surface on the atomic scale, but still too close to the solid to be influenced by ambient electric fields in the vacuum. The work function is not a characteristic of a bulk material, but rather a property of the surface of the material (depending on crystal face and contamination). Definition The work function for a given surface is defined by the difference :W = -e\phi - E_, where is the charge of an electron, is the electrostatic potential in the vacuum nearby the surface, and is the Fermi level ( electrochemical potential of electrons) inside the material. The term is the energy of an electron at rest in the vacuum nearby the surface. In practice, one directly controls ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electrostatic Potential
Electrostatics is a branch of physics that studies electric charges at rest (static electricity). Since classical times, it has been known that some materials, such as amber, attract lightweight particles after rubbing. The Greek word for amber, (), was thus the source of the word 'electricity'. Electrostatic phenomena arise from the forces that electric charges exert on each other. Such forces are described by Coulomb's law. Even though electrostatically induced forces seem to be rather weak, some electrostatic forces are relatively large. The force between an electron and a proton, which together make up a hydrogen atom, is about 36 orders of magnitude stronger than the gravitational force acting between them. There are many examples of electrostatic phenomena, from those as simple as the attraction of plastic wrap to one's hand after it is removed from a package, to the apparently spontaneous explosion of grain silos, the damage of electronic components during manufactu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |