|
Bach Or Stravinsky
In game theory, the battle of the sexes is a two-player coordination game that also involves elements of conflict. The game was introduced in 1957 by R. Duncan Luce and Howard Raiffa in their classic book, ''Games and Decisions''. Some authors prefer to avoid assigning sexes to the players and instead use Players 1 and 2, and some refer to the game as Bach or Stravinsky, using two concerts as the two events. The game description here follows Luce and Raiffa's original story. Imagine that a man and a woman hope to meet this evening, but have a choice between two events to attend: a prize fight and a ballet. The man would prefer to go to prize fight. The woman would prefer the ballet. Both would prefer to go to the same event rather than different ones. If they cannot communicate, where should they go? The payoff matrix labeled "Battle of the Sexes (1)" shows the payoffs when the man chooses a row and the woman chooses a column. In each cell, the first number represents the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions among rational agents. Myerson, Roger B. (1991). ''Game Theory: Analysis of Conflict,'' Harvard University Press, p.&nbs1 Chapter-preview links, ppvii–xi It has applications in all fields of social science, as well as in logic, systems science and computer science. Originally, it addressed two-person zero-sum games, in which each participant's gains or losses are exactly balanced by those of other participants. In the 21st century, game theory applies to a wide range of behavioral relations; it is now an umbrella term for the science of logical decision making in humans, animals, as well as computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum game and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathema ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordination Game
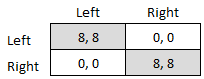
A coordination game is a type of simultaneous game found in game theory. It describes the situation where a player will earn a higher payoff when they select the same course of action as another player. The game is not one of pure conflict, which results in multiple pure strategy Nash equilibria in which players choose matching strategies. Figure 1 shows a 2-player example. Both (Up, Left) and (Down, Right) are Nash equilibria. If the players expect (Up, Left) to be played, then player 1 thinks their payoff would fall from 2 to 1 if they deviated to Down, and player 2 thinks their payoff would fall from 4 to 3 if they chose Right. If the players expect (Down, Right), player 1 thinks their payoff would fall from 2 to 1 if they deviated to Up, and player 2 thinks their payoff would fall from 4 to 3 if they chose Left. A player's optimal move depends on what they expect the other player to do, and they both do better if they coordinate than if they played an off-equilibrium combinat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Howard Raiffa
Howard Raiffa (; January 24, 1924 – July 8, 2016) was an American academic who was the Frank P. Ramsey Professor (Emeritus) of Managerial Economics, a joint chair held by the Business School and Harvard Kennedy School at Harvard University. He was an influential Bayesian decision theorist and pioneer in the field of decision analysis, with works in statistical decision theory, game theory, behavioral decision theory, risk analysis, and negotiation analysis. He helped found and was the first director of the International Institute for Applied Systems Analysis. Early life After service in the Army Air Forces during World War II, Raiffa received a bachelor's degree in mathematics in 1946, a master's degree in statistics in 1947 and a PhD in mathematics in 1951, all from the University of Michigan. Career *His book ''Applied Statistical Decision Theory'' with Robert Schlaifer introduced the idea of conjugate prior distributions. *A lecture of his in the 1960s concerning the use o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Boxing
Boxing (also known as "Western boxing" or "pugilism") is a combat sport in which two people, usually wearing protective gloves and other protective equipment such as hand wraps and mouthguards, throw punches at each other for a predetermined amount of time in a boxing ring. Although the term "boxing" is commonly attributed to "western boxing", in which only the fists are involved, boxing has developed in various ways in different geographical areas and cultures. In global terms, boxing is a set of combat sports focused on striking, in which two opponents face each other in a fight using at least their fists, and possibly involving other actions such as kicks, elbow strikes, Knee (strike), knee strikes, and headbutts, depending on the rules. Some of the forms of the modern sport are western boxing, Bare-knuckle boxing, bare knuckle boxing, kickboxing, Muay Thai, muay-thai, lethwei, savate, and Sanda (sport), sanda. Boxing techniques have been incorporated into many martial ar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ballet
Ballet () is a type of performance dance that originated during the Italian Renaissance in the fifteenth century and later developed into a concert dance form in France and Russia. It has since become a widespread and highly technical form of dance with its own vocabulary. Ballet has been influential globally and has defined the foundational techniques which are used in many other dance genres and cultures. Various schools around the world have incorporated their own cultures. As a result, ballet has evolved in distinct ways. A ''ballet'' as a unified work comprises the choreography and music for a ballet production. Ballets are choreographed and performed by trained ballet dancers. Traditional classical ballets are usually performed with classical music accompaniment and use elaborate costumes and staging, whereas modern ballets are often performed in simple costumes and without elaborate sets or scenery. Etymology Ballet is a French word which had its origin in Italian ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Payoff Matrix
In game theory, normal form is a description of a ''game''. Unlike extensive form, normal-form representations are not graphical ''per se'', but rather represent the game by way of a matrix. While this approach can be of greater use in identifying strictly dominated strategies and Nash equilibria, some information is lost as compared to extensive-form representations. The normal-form representation of a game includes all perceptible and conceivable strategies, and their corresponding payoffs, for each player. In static games of complete, perfect information, a normal-form representation of a game is a specification of players' strategy spaces and payoff functions. A strategy space for a player is the set of all strategies available to that player, whereas a strategy is a complete plan of action for every stage of the game, regardless of whether that stage actually arises in play. A payoff function for a player is a mapping from the cross-product of players' strategy spaces to that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pure Strategy
In game theory, a player's strategy is any of the options which they choose in a setting where the outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship. A player's strategy will determine the action which the player will take at any stage of the game. In studying game theory, economists enlist a more rational lens in analyzing decisions rather than the psychological or sociological perspectives taken when analyzing relationships between decisions of two or more parties in different disciplines. The strategy concept is sometimes (wrongly) confused with that of a move. A move is an action taken by a player at some point during the play of a game (e.g., in chess, moving white's Bishop a2 to b3). A strategy on the other hand is a complete algorithm for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nash Equilibria
In game theory, the Nash equilibrium, named after the mathematician John Nash, is the most common way to define the solution of a non-cooperative game involving two or more players. In a Nash equilibrium, each player is assumed to know the equilibrium strategies of the other players, and no one has anything to gain by changing only one's own strategy. The principle of Nash equilibrium dates back to the time of Cournot, who in 1838 applied it to competing firms choosing outputs. If each player has chosen a strategy an action plan based on what has happened so far in the game and no one can increase one's own expected payoff by changing one's strategy while the other players keep their's unchanged, then the current set of strategy choices constitutes a Nash equilibrium. If two players Alice and Bob choose strategies A and B, (A, B) is a Nash equilibrium if Alice has no other strategy available that does better than A at maximizing her payoff in response to Bob choosing B, and Bob ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mixed Strategy
In game theory, a player's strategy is any of the options which they choose in a setting where the outcome depends ''not only'' on their own actions ''but'' on the actions of others. The discipline mainly concerns the action of a player in a game affecting the behavior or actions of other players. Some examples of "games" include chess, bridge, poker, monopoly, diplomacy or battleship. A player's strategy will determine the action which the player will take at any stage of the game. In studying game theory, economists enlist a more rational lens in analyzing decisions rather than the psychological or sociological perspectives taken when analyzing relationships between decisions of two or more parties in different disciplines. The strategy concept is sometimes (wrongly) confused with that of a move. A move is an action taken by a player at some point during the play of a game (e.g., in chess, moving white's Bishop a2 to b3). A strategy on the other hand is a complete algorithm for p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Correlated Equilibrium
In game theory, a correlated equilibrium is a solution concept that is more general than the well known Nash equilibrium. It was first discussed by mathematician Robert Aumann in 1974. The idea is that each player chooses their action according to their private observation of the value of the same public signal. A strategy assigns an action to every possible observation a player can make. If no player would want to deviate from their strategy (assuming the others also don't deviate), the distribution from which the signals are drawn is called a correlated equilibrium. Formal definition An N-player strategic game \displaystyle (N,A_i,u_i) is characterized by an action set A_i and utility function u_i for each player i. When player i chooses strategy a_i \in A_i and the remaining players choose a strategy profile described by the N-1-tuple a_, then player i's utility is \displaystyle u_i(a_i,a_). A ''strategy modification'' for player i is a function \phi_i\colon A_i \to A_i. That ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Money Burning
Money burning or burning money is the purposeful act of destroying money. In the prototypical example, banknotes are destroyed by setting them on fire. Burning money decreases the wealth of the owner without directly enriching any particular party. It also reduces the money supply and (very slightly) slows down the inflation rate. Money is usually burned to communicate a message, either for artistic effect, as a form of protest, or as a signal. In some games, a player can sometimes benefit from the ability to burn money (battle of the sexes). The burning of money is illegal in some jurisdictions. Macroeconomic effect For the purposes of macroeconomics, burning money is equivalent to removing the money from circulation, and locking it away forever; the salient feature is that no one may ever use the money again. Burning money shrinks the money supply, and is therefore a special case of contractionary monetary policy that can be implemented by anyone. In the usual case, the centr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dominance (game Theory)
In game theory, strategic dominance (commonly called simply dominance) occurs when one strategy is better than another strategy for one player, no matter how that player's opponents may play. Many simple games can be solved using dominance. The opposite, intransitivity, occurs in games where one strategy may be better or worse than another strategy for one player, depending on how the player's opponents may play. Terminology When a player tries to choose the "best" strategy among a multitude of options, that player may compare two strategies A and B to see which one is better. The result of the comparison is one of: * B is equivalent to A: choosing B always gives the same outcome as choosing A, no matter what the other players do. * B strictly dominates A: choosing B always gives a better outcome than choosing A, no matter what the other players do. * B weakly dominates A: choosing B always gives at least as good an outcome as choosing A, no matter what the other players do, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |