|
Aurifeuillean Factorization
In number theory, an aurifeuillean factorization, named after Léon-François-Antoine Aurifeuille, is a special type of algebraic factorization that comes from non-trivial factorizations of cyclotomic polynomials over the integers. Although cyclotomic polynomials themselves are irreducible over the integers, when restricted to particular integer values they may have an algebraic factorization, as in the examples below. Examples * Numbers of the form a^4 + 4b^4 have the following aurifeuillean factorization (see also Sophie Germain's identity): :: a^4 + 4b^4 = (a^2 - 2ab + 2b^2)\cdot (a^2 + 2ab + 2b^2) * Setting a=1 and b=2^k, one obtains the following aurifeuillean factorization of 2^+1: :: 2^+1 = (2^-2^+1)\cdot (2^+2^+1) * Numbers of the form b^n - 1 or \Phi_n(b), where b = s^2 \cdot t with square-free t, have aurifeuillean factorization if and only if one of the following conditions holds: ** t\equiv 1 \pmod 4 and n\equiv t \pmod ** t\equiv 2, 3 \pmod 4 and n\equiv 2t \pmo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
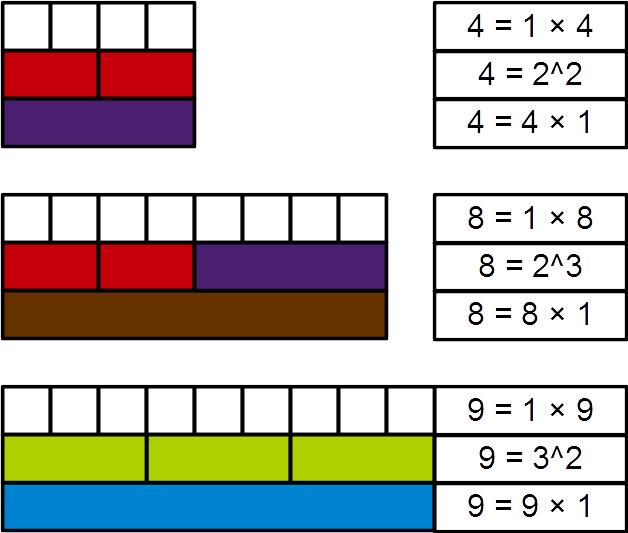
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mersenne Prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If is a composite number then so is . Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form for some prime . The exponents which give Mersenne primes are 2, 3, 5, 7, 13, 17, 19, 31, ... and the resulting Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, ... . Numbers of the form without the primality requirement may be called Mersenne numbers. Sometimes, however, Mersenne numbers are defined to have the additional requirement that be prime. The smallest composite Mersenne number with prime exponent ''n'' is . Mersenne primes were studied in antiquity because of their close connection to perfect numbers: the Euclid–Euler theorem as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Édouard Lucas
__NOTOC__ François Édouard Anatole Lucas (; 4 April 1842 – 3 October 1891) was a French mathematician. Lucas is known for his study of the Fibonacci sequence. The related Lucas sequences and Lucas numbers are named after him. Biography Lucas was born in Amiens and educated at the École Normale Supérieure. He worked in the Paris Observatory and later became a professor of mathematics at the Lycée Saint Louis and the Lycée Charlemagne in Paris. Lucas served as an artillery officer in the French Army during the Franco-Prussian War of 1870–1871. In 1875, Lucas posed a challenge to prove that the only solution of the Diophantine equation: :\sum_^ n^2 = M^2\; with ''N'' > 1 is when ''N'' = 24 and ''M'' = 70. This is known as the cannonball problem, since it can be visualized as the problem of taking a square arrangement of cannonballs on the ground and building a square pyramid out of them. It was not until 1918 that a proof (using elliptic functions) was found for t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow method of checking the primality of a given number n, called trial division, tests whether n is a multiple of any integer between 2 and \sqrt. Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error, and the AKS primality test, which always pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Pages
The PrimePages is a website about prime numbers maintained by Chris Caldwell at the University of Tennessee at Martin. The site maintains the list of the "5,000 largest known primes", selected smaller primes of special forms, and many "top twenty" lists for primes of various forms. , the 5,000th prime has around 412,000 digits.. Retrieved on 2018-02-12. The PrimePages has articles on primes and primality testing. It includes "The Prime Glossary" with articles on hundreds of glosses related to primes, and "Prime Curios!" with thousands of curios about specific numbers. The database started as a list of titanic primes (primes with at least 1000 decimal digits) by Samuel Yates. In subsequent years, the whole top-5,000 has consisted of gigantic primes (primes with at least 10,000 decimal digits). Primes of special forms are kept on the current lists if they are titanic and in the top-20 or top-5 for their form. See also *List of prime numbers This is a list of articles about pri ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Number
In mathematics, the Fibonacci numbers, commonly denoted , form a sequence, the Fibonacci sequence, in which each number is the sum of the two preceding ones. The sequence commonly starts from 0 and 1, although some authors start the sequence from 1 and 1 or sometimes (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the first few values in the sequence are: :0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144. The Fibonacci numbers were first described in Indian mathematics, as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, later known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book ''Liber Abaci''. Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the ''Fibonacci Quarterly''. Applications of Fibonacci numbers include co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lucas Number
The Lucas numbers or Lucas series are an integer sequence named after the mathematician François Édouard Anatole Lucas (1842–1891), who studied both that sequence and the closely related Fibonacci numbers. Lucas numbers and Fibonacci numbers form complementary instances of Lucas sequences. The Lucas series has the same recursive relationship as the Fibonacci sequence, where each term is the sum of the two previous terms, but with different starting values. This produces a sequence where the ratios of successive terms approach the golden ratio, and in fact the terms themselves are roundings of integer powers of the golden ratio. The sequence also has a variety of relationships with the Fibonacci numbers, like the fact that adding any two Fibonacci numbers two terms apart in the Fibonacci sequence results in the Lucas number in between. The first few Lucas numbers are : 2, 1, 3, 4, 7, 11, 18, 29, 47, 76, 123, 199, 322, 521, 843, 1364, 2207, 3571, 5778, 9349 .... Defini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polynomial
In mathematics, a polynomial is an expression consisting of indeterminates (also called variables) and coefficients, that involves only the operations of addition, subtraction, multiplication, and positive-integer powers of variables. An example of a polynomial of a single indeterminate is . An example with three indeterminates is . Polynomials appear in many areas of mathematics and science. For example, they are used to form polynomial equations, which encode a wide range of problems, from elementary word problems to complicated scientific problems; they are used to define polynomial functions, which appear in settings ranging from basic chemistry and physics to economics and social science; they are used in calculus and numerical analysis to approximate other functions. In advanced mathematics, polynomials are used to construct polynomial rings and algebraic varieties, which are central concepts in algebra and algebraic geometry. Etymology The word ''polynomial'' join ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coefficient
In mathematics, a coefficient is a multiplicative factor in some term of a polynomial, a series, or an expression; it is usually a number, but may be any expression (including variables such as , and ). When the coefficients are themselves variables, they may also be called parameters. For example, the polynomial 2x^2-x+3 has coefficients 2, −1, and 3, and the powers of the variable x in the polynomial ax^2+bx+c have coefficient parameters a, b, and c. The constant coefficient is the coefficient not attached to variables in an expression. For example, the constant coefficients of the expressions above are the number 3 and the parameter ''c'', respectively. The coefficient attached to the highest degree of the variable in a polynomial is referred to as the leading coefficient. For example, in the expressions above, the leading coefficients are 2 and ''a'', respectively. Terminology and definition In mathematics, a coefficient is a multiplicative factor in some term of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Léon-François-Antoine Aurifeuille
Léon-François-Antoine Aurifeuille (1822–1882) was a French mathematician after whom Aurifeuillean factorizations are named. He was the author of three books: ''Cours de géométrie élémentaire'' (with C. Richaud, Paris: Bachelier, 1847), ''Traité de géométrie élémentaire'' (with C. Dumont, 2nd ed., Toulouse: Bonnal & Gibrac, 1860), and ''Traité d'arithmétique'' (with C. Dumont, 2nd ed., Toulouse: Bonnal & Gibrac, 1859). Under the pseudonym A pseudonym (; ) or alias () is a fictitious name that a person or group assumes for a particular purpose, which differs from their original or true name (orthonym). This also differs from a new name that entirely or legally replaces an individua ... Alfred de Caston, French National Library, retrieved 2015-03-05. he also wrote several other books, including ''Les Tricheurs, sc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |