|
Archimedes Number
In viscous fluid dynamics, the Archimedes number (Ar), is a dimensionless number used to determine the motion of fluids due to density differences, named after the ancient Greek scientist and mathematician Archimedes. It is the ratio of gravitational forces to viscous forces and has the form: :\begin\mathrm & = \frac \\ & = \frac \\ \end where: * g is the local external field (for example gravitational acceleration), , * L is the characteristic length of body, . * \frac is the submerged specific gravity, * \rho_\ell is the density of the fluid, , * \rho is the density of the body, , * \nu = \frac is the kinematic viscosity, , * \mu is the dynamic viscosity, , Uses The Archimedes number is generally used in design of tubular chemical process reactors. The following are non-exhaustive examples of using the Archimedes number in reactor design. Packed-bed fluidization design The Archimedes number is applied often in the engineering of packed beds, which are very common in th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fluid Dynamics
In physics and engineering, fluid dynamics is a subdiscipline of fluid mechanics that describes the flow of fluids—liquids and gases. It has several subdisciplines, including '' aerodynamics'' (the study of air and other gases in motion) and hydrodynamics (the study of liquids in motion). Fluid dynamics has a wide range of applications, including calculating forces and moments on aircraft, determining the mass flow rate of petroleum through pipelines, predicting weather patterns, understanding nebulae in interstellar space and modelling fission weapon detonation. Fluid dynamics offers a systematic structure—which underlies these practical disciplines—that embraces empirical and semi-empirical laws derived from flow measurement and used to solve practical problems. The solution to a fluid dynamics problem typically involves the calculation of various properties of the fluid, such as flow velocity, pressure, density, and temperature, as functions of space a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Working Fluid
For fluid power, a working fluid is a gas or liquid that primarily transfers force, motion, or mechanical energy. In hydraulics, water or hydraulic fluid transfers force between hydraulic components such as hydraulic pumps, hydraulic cylinders, and hydraulic motors that are assembled into hydraulic machinery, hydraulic drive systems, etc. In pneumatics, the working fluid is air or another gas which transfers force between pneumatic components such as compressors, vacuum pumps, pneumatic cylinders, and pneumatic motors. In pneumatic systems, the working gas also stores energy because it is compressible. (Gases also heat up as they are compressed and cool as they expand; this incidental heat pump is rarely exploited.) (Some gases also condense into liquids as they are compressed and boil as pressure is reduced.) For passive heat transfer, a working fluid is a gas or liquid, usually called a coolant or heat transfer fluid, that primarily transfers heat into or out of a region of i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Galilei Number
In fluid dynamics, the Galilei number (Ga), sometimes also referred to as Galileo number (see discussion), is a dimensionless number named after Italian scientist Galileo Galilei (1564-1642). It may be regarded as proportional to gravity forces divided by viscous forces. The Galilei number is used in viscous flow and thermal expansion calculations, for example to describe fluid film flow over walls. These flows apply to condensers or chemical columns. : \mathrm = \frac * ''g'': gravitational acceleration, ( SI units: m/ s2) * ''L'': characteristic length, ( SI units: m) * ''ν'': characteristic kinematic viscosity, ( SI units: m2/s) See also *Archimedes number In viscous fluid dynamics, the Archimedes number (Ar), is a dimensionless number used to determine the motion of fluids due to density differences, named after the ancient Greek scientist and mathematician Archimedes. It is the ratio of gravitati ... References *VDI-Wärmeatlas; 5., extended Edition; VDI Verlag Düs ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimensionless Quantity
A dimensionless quantity (also known as a bare quantity, pure quantity, or scalar quantity as well as quantity of dimension one) is a quantity to which no physical dimension is assigned, with a corresponding SI unit of measurement of one (or 1), ISBN 978-92-822-2272-0. which is not explicitly shown. Dimensionless quantities are widely used in many fields, such as mathematics, physics, chemistry, engineering, and economics. Dimensionless quantities are distinct from quantities that have associated dimensions, such as time (measured in seconds). Dimensionless units are dimensionless values that serve as units of measurement for expressing other quantities, such as radians (rad) or steradians (sr) for plane angles and solid angles, respectively. For example, optical extent is defined as having units of metres multiplied by steradians. History Quantities having dimension one, ''dimensionless quantities'', regularly occur in sciences, and are formally treated within the fie ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convection (heat Transfer)
Convection (or convective heat transfer) is the transfer of heat from one place to another due to the movement of fluid. Although often discussed as a distinct method of heat transfer, convective heat transfer involves the combined processes of conduction (heat diffusion) and advection (heat transfer by bulk fluid flow). Convection is usually the dominant form of heat transfer in liquids and gases. Note that this definition of convection is only applicable in Heat transfer and thermodynamic contexts. It should not to be confused with the dynamic fluid phenomenon of convection, which is typically referred to as ''Natural Convection'' in thermodynamic contexts in order to distinguish the two. Overview Convection can be "forced" by movement of a fluid by means other than buoyancy forces (for example, a water pump in an automobile engine). Thermal expansion of fluids may also force convection. In other cases, natural buoyancy forces alone are entirely responsible for fluid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
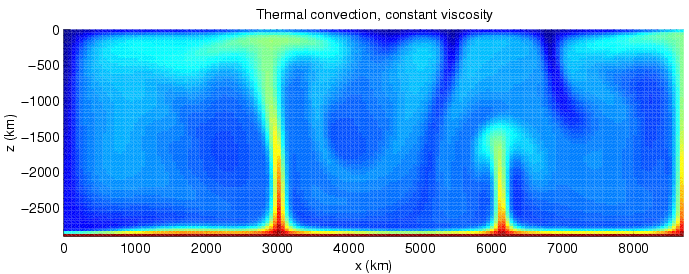
Convection
Convection is single or multiphase fluid flow that occurs spontaneously due to the combined effects of material property heterogeneity and body forces on a fluid, most commonly density and gravity (see buoyancy). When the cause of the convection is unspecified, convection due to the effects of thermal expansion and buoyancy can be assumed. Convection may also take place in soft solids or mixtures where particles can flow. Convective flow may be transient (such as when a multiphase mixture of oil and water separates) or steady state (see Convection cell). The convection may be due to gravitational, electromagnetic or fictitious body forces. Heat transfer by natural convection plays a role in the structure of Earth's atmosphere, its oceans, and its mantle. Discrete convective cells in the atmosphere can be identified by clouds, with stronger convection resulting in thunderstorms. Natural convection also plays a role in stellar physics. Convection is often cate ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stokes Flow
Stokes flow (named after George Gabriel Stokes), also named creeping flow or creeping motion,Kim, S. & Karrila, S. J. (2005) ''Microhydrodynamics: Principles and Selected Applications'', Dover. . is a type of fluid flow where advective inertial forces are small compared with viscous forces. The Reynolds number is low, i.e. \mathrm \ll 1. This is a typical situation in flows where the fluid velocities are very slow, the viscosities are very large, or the length-scales of the flow are very small. Creeping flow was first studied to understand lubrication. In nature this type of flow occurs in the swimming of microorganisms, sperm and the flow of lava. In technology, it occurs in paint, MEMS devices, and in the flow of viscous polymers generally. The equations of motion for Stokes flow, called the Stokes equations, are a linearization of the Navier–Stokes equations, and thus can be solved by a number of well-known methods for linear differential equations. The primary Green's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Artificial Neural Network
Artificial neural networks (ANNs), usually simply called neural networks (NNs) or neural nets, are computing systems inspired by the biological neural networks that constitute animal brains. An ANN is based on a collection of connected units or nodes called artificial neurons, which loosely model the neurons in a biological brain. Each connection, like the synapses in a biological brain, can transmit a signal to other neurons. An artificial neuron receives signals then processes them and can signal neurons connected to it. The "signal" at a connection is a real number, and the output of each neuron is computed by some non-linear function of the sum of its inputs. The connections are called ''edges''. Neurons and edges typically have a ''weight'' that adjusts as learning proceeds. The weight increases or decreases the strength of the signal at a connection. Neurons may have a threshold such that a signal is sent only if the aggregate signal crosses that threshold. Typically, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
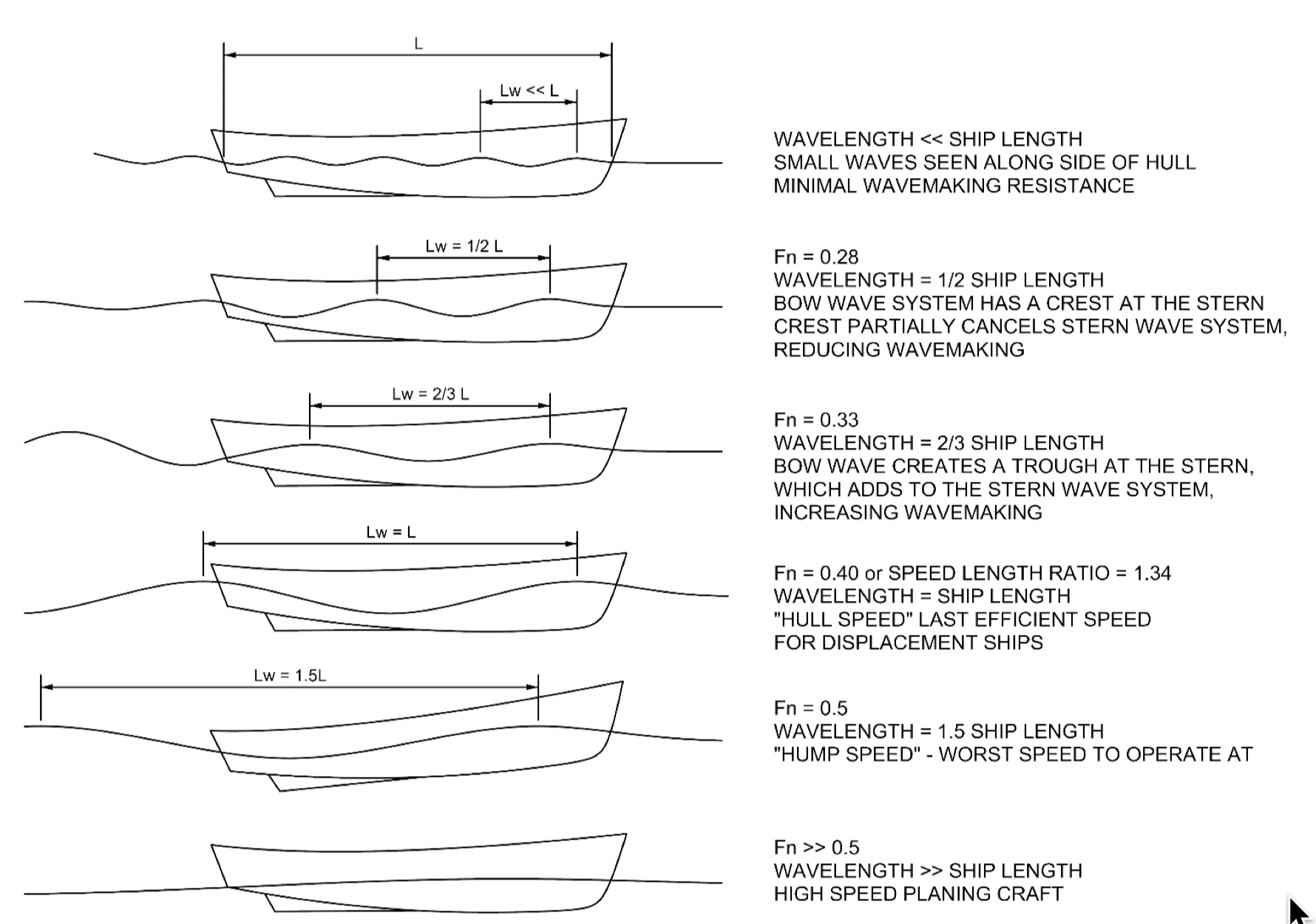
Froude Number
In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on the speed–length ratio which he defined as: \mathrm = \frac where is the local flow velocity, is the local external field, and is a characteristic length. The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations. However, in naval architecture the Froude number is a significant figure used to determine the resistance of a partially submerged object moving through water. Origins In open channel flows, introduced first ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Eötvös Number
In fluid dynamics the Eötvös number (Eo), also called the Bond number (Bo), is a dimensionless number measuring the importance of gravitational forces compared to surface tension forces for the movement of liquid front. Alongside the Capillary number, commonly denoted Ca, which represents the contribution of viscous drag, Bo is useful for studying the movement of fluid in porous or granular media, such as soil.Dynamics of viscous entrapped saturated zones in partially wetted porous media Transport in Porous Media (2018), 125(2), 193-210 The Bond number (or Eötvös number) is also used (together with ) to characteriz ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bubble Column Reactor
A bubble column reactor is an apparatus used to generate and control gas-liquid chemical reactions. It consists of a vertically-arranged cylindrical column filled with liquid, at the bottom of which gas is inserted. Principle The introduction of gas takes place at the bottom of the column and causes a turbulent stream to enable an optimum gas exchange. Numerous forms of construction exist. The mixing is done by the gas sparging and it requires less energy than mechanical stirring. The liquid can be in parallel flow or counter-current. Bubble column reactors are characterized by a high liquid content and a moderate phase boundary surface. The bubble column is particularly useful in reactions where the gas-liquid reaction is slow in relation to the absorption rate. This is the case for gas-liquid reactions with a Hatta number Ha <0.3. Bubble column reactors are used in various types of chemical reactions like |