|
Apparent Diffusion Coefficient
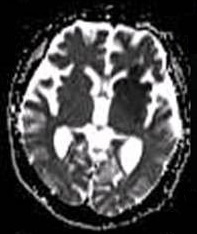
Diffusion-weighted magnetic resonance imaging (DWI or DW-MRI) is the use of specific MRI sequences as well as software that generates images from the resulting data that uses the diffusion of water molecules to generate contrast in MR images. It allows the mapping of the diffusion process of molecules, mainly water, in biological tissues, in vivo and non-invasively. Molecular diffusion in tissues is not random, but reflects interactions with many obstacles, such as macromolecules, fibers, and membranes. Water molecule diffusion patterns can therefore reveal microscopic details about tissue architecture, either normal or in a diseased state. A special kind of DWI, diffusion tensor imaging (DTI), has been used extensively to map white matter tractography in the brain. Introduction In diffusion weighted imaging (DWI), the intensity of each image element ( voxel) reflects the best estimate of the rate of water diffusion at that location. Because the mobility of water is driven ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
MRI Sequence
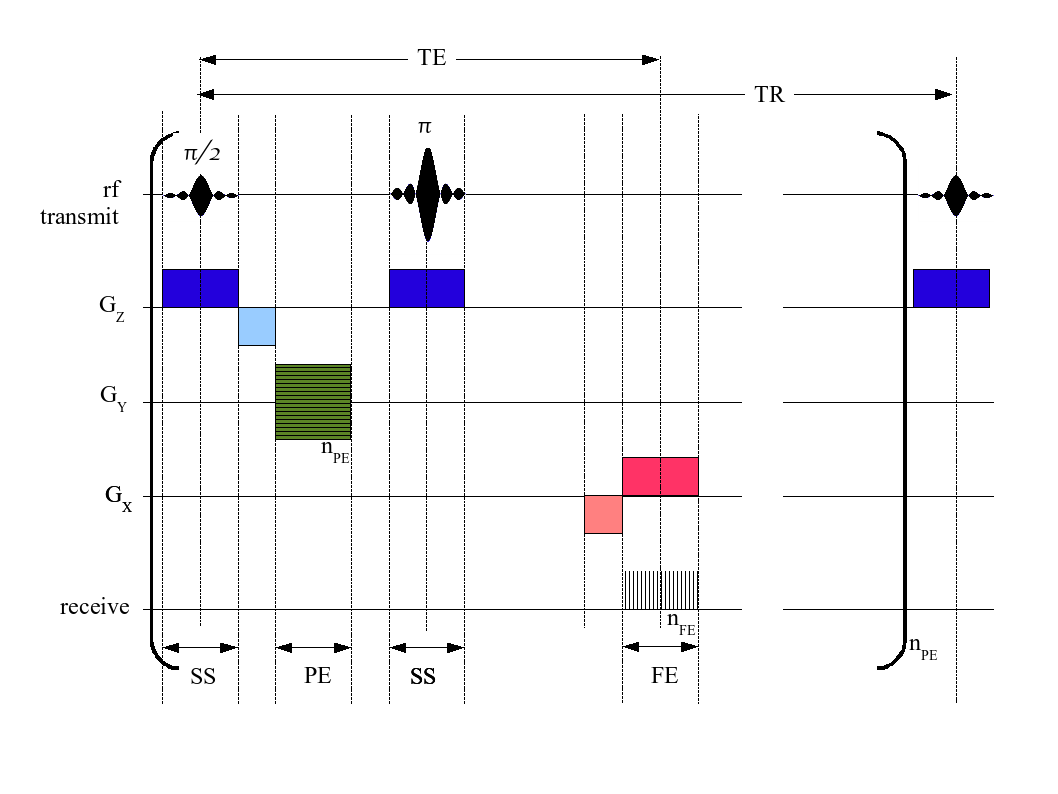
An MRI sequence in magnetic resonance imaging (MRI) is a particular setting of pulse sequences and pulsed field gradients, resulting in a particular image appearance. A multiparametric MRI is a combination of two or more sequences, and/or including other specialized MRI configurations such as spectroscopy. Spin echo T1 and T2 Each tissue returns to its equilibrium state after excitation by the independent relaxation processes of T1 ( spin-lattice; that is, magnetization in the same direction as the static magnetic field) and T2 ( spin-spin; transverse to the static magnetic field). To create a T1-weighted image, magnetization is allowed to recover before measuring the MR signal by changing the repetition time (TR). This image weighting is useful for assessing the cerebral cortex, identifying fatty tissue, characterizing focal liver lesions, and in general, obtaining morphological information, as well as for post-contrast imaging. To create a T2-weighted image, magnetizati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axons
An axon (from Greek ἄξων ''áxōn'', axis), or nerve fiber (or nerve fibre: see American and British English spelling differences#-re, -er, spelling differences), is a long, slender projection of a nerve cell, or neuron, in vertebrates, that typically conducts electrical impulses known as action potentials away from the Soma (biology), nerve cell body. The function of the axon is to transmit information to different neurons, muscles, and glands. In certain sensory neurons (pseudounipolar neurons), such as those for touch and warmth, the axons are called afferent nerve fibers and the electrical impulse travels along these from the peripheral nervous system, periphery to the cell body and from the cell body to the spinal cord along another branch of the same axon. Axon dysfunction can be the cause of many inherited and acquired neurological disorders that affect both the Peripheral nervous system, peripheral and Central nervous system, central neurons. Nerve fibers are Axon#Cl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation, when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. The equation above applies wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divergence
In vector calculus, divergence is a vector operator that operates on a vector field, producing a scalar field giving the quantity of the vector field's source at each point. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around a given point. As an example, consider air as it is heated or cooled. The velocity of the air at each point defines a vector field. While air is heated in a region, it expands in all directions, and thus the velocity field points outward from that region. The divergence of the velocity field in that region would thus have a positive value. While the air is cooled and thus contracting, the divergence of the velocity has a negative value. Physical interpretation of divergence In physical terms, the divergence of a vector field is the extent to which the vector field flux behaves like a source at a given point. It is a local measure of its "outgoingness" – the extent to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuity Equation
A continuity equation or transport equation is an equation that describes the transport of some quantity. It is particularly simple and powerful when applied to a conserved quantity, but it can be generalized to apply to any extensive quantity. Since mass, energy, momentum, electric charge and other natural quantities are conserved under their respective appropriate conditions, a variety of physical phenomena may be described using continuity equations. Continuity equations are a stronger, local form of conservation laws. For example, a weak version of the law of conservation of energy states that energy can neither be created nor destroyed—i.e., the total amount of energy in the universe is fixed. This statement does not rule out the possibility that a quantity of energy could disappear from one point while simultaneously appearing at another point. A stronger statement is that energy is ''locally'' conserved: energy can neither be created nor destroyed, ''nor'' can it " t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Coefficient
Diffusivity, mass diffusivity or diffusion coefficient is a proportionality constant between the molar flux due to molecular diffusion and the gradient in the concentration of the species (or the driving force for diffusion). Diffusivity is encountered in Fick's law and numerous other equations of physical chemistry. The diffusivity is generally prescribed for a given pair of species and pairwise for a multi-species system. The higher the diffusivity (of one substance with respect to another), the faster they diffuse into each other. Typically, a compound's diffusion coefficient is ~10,000× as great in air as in water. Carbon dioxide in air has a diffusion coefficient of 16 mm2/s, and in water its diffusion coefficient is 0.0016 mm2/s. Diffusivity has dimensions of length2 / time, or m2/s in SI units and cm2/s in CGS units. Temperature dependence of the diffusion coefficient Solids The diffusion coefficient in solids at different temperatures is generally found ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gradient of a function is non-zero at a point , the direction of the gradient is the direction in which the function increases most quickly from , and the magnitude of the gradient is the rate of increase in that direction, the greatest absolute directional derivative. Further, a point where the gradient is the zero vector is known as a stationary point. The gradient thus plays a fundamental role in optimization theory, where it is used to maximize a function by gradient ascent. In coordinate-free terms, the gradient of a function f(\bf) may be defined by: :df=\nabla f \cdot d\bf where ''df'' is the total infinitesimal change in ''f'' for an infinitesimal displacement d\bf, and is seen to be maximal when d\bf is in the direction of the gradi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fick's Laws Of Diffusion
Fick's laws of diffusion describe diffusion and were derived by Adolf Fick in 1855. They can be used to solve for the diffusion coefficient, . Fick's first law can be used to derive his second law which in turn is identical to the diffusion equation. A diffusion process that obeys Fick's laws is called normal or Fickian diffusion; otherwise, it is called anomalous diffusion or non-Fickian diffusion. History In 1855, physiologist Adolf Fick first reported* * his now well-known laws governing the transport of mass through diffusive means. Fick's work was inspired by the earlier experiments of Thomas Graham, which fell short of proposing the fundamental laws for which Fick would become famous. Fick's law is analogous to the relationships discovered at the same epoch by other eminent scientists: Darcy's law (hydraulic flow), Ohm's law (charge transport), and Fourier's Law (heat transport). Fick's experiments (modeled on Graham's) dealt with measuring the concentrations and f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gyromagnetic Ratio
In physics, the gyromagnetic ratio (also sometimes known as the magnetogyric ratio in other disciplines) of a particle or system is the ratio of its magnetic moment to its angular momentum, and it is often denoted by the symbol , gamma. Its SI unit is the radian per second per tesla (rad⋅s−1⋅T−1) or, equivalently, the coulomb per kilogram (C⋅kg−1). The term "gyromagnetic ratio" is often used as a synonym for a ''different'' but closely related quantity, the -factor. The -factor only differs from the gyromagnetic ratio in being dimensionless. For a classical rotating body Consider a nonconductive charged body rotating about an axis of symmetry. According to the laws of classical physics, it has both a magnetic dipole moment due to the movement of charge and an angular momentum due to the movement of mass arising from its rotation. It can be shown that as long as its charge and mass density and flow are distributed identically and rotationally symmetric, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moiety (chemistry)
In organic chemistry, a moiety ( ) is a part of a molecule that is given a name because it is identified as a part of other molecules as well. Typically, the term is used to describe the larger and characteristic parts of organic molecules, and it should not be used to describe or name smaller functional groups of atoms that chemically react in similar ways in most molecules that contain them. Occasionally, a moiety may contain smaller moieties and functional groups. A moiety that acts as a branch extending from the backbone of a hydrocarbon molecule is called a substituent or side chain, which typically can be removed from the molecule and substituted with others. Active moiety In pharmacology, an active moiety is the part of a molecule or ion – excluding appended inactive portions – that is responsible for the physiological or pharmacological action of a drug substance. Inactive appended portions of the drug substance may include either the alcohol or acid moiety of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fractional Anisotropy
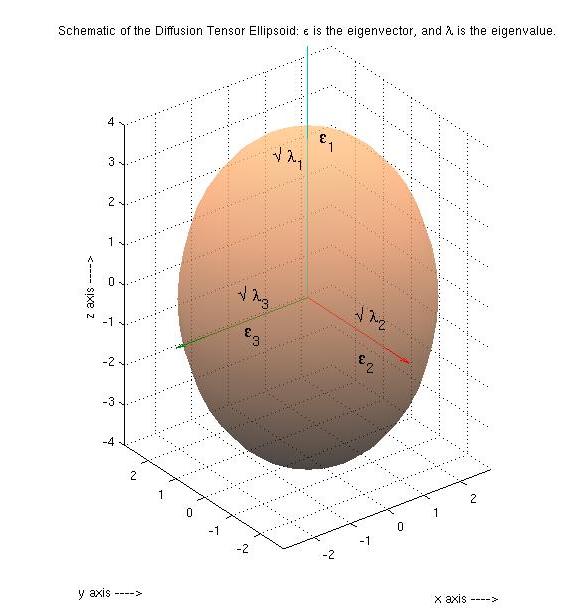
Fractional anisotropy (FA) is a scalar value between zero and one that describes the degree of anisotropy of a diffusion process. A value of zero means that diffusion is isotropic, i.e. it is unrestricted (or equally restricted) in all directions. A value of one means that diffusion occurs only along one axis and is fully restricted along all other directions. FA is a measure often used in diffusion imaging where it is thought to reflect fiber density, axonal diameter, and myelination in white matter. The FA is an extension of the concept of eccentricity of conic sections in 3 dimensions, normalized to the unit range. Definition A Diffusion Ellipsoid is completely represented by the Diffusion Tensor, D. FA is calculated from the eigenvalues (\lambda_1, \lambda_2, \lambda_3) of the diffusion tensor. The eigenvectors \epsilon give the directions in which the ellipsoid has major axes, and the corresponding eigenvalues \lambda give the magnitude of the peak in that direction. : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tensors. There are many types of tensors, including scalars and vectors (which are the simplest tensors), dual vectors, multilinear maps between vector spaces, and even some operations such as the dot product. Tensors are defined independent of any basis, although they are often referred to by their components in a basis related to a particular coordinate system. Tensors have become important in physics because they provide a concise mathematical framework for formulating and solving physics problems in areas such as mechanics (stress, elasticity, fluid mechanics, moment of inertia, ...), electrodynamics (electromagnetic tensor, Maxwell tensor, permittivity, magnetic susceptibility, ...), general relativity ( stress–energy tensor, cur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |