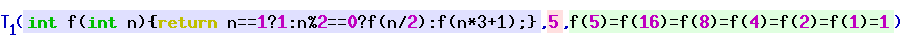|
Admissible Numbering
In computability theory, admissible numberings are enumerations ( numberings) of the set of partial computable functions that can be converted ''to and from'' the standard numbering. These numberings are also called acceptable numberings and acceptable programming systems. Rogers' equivalence theorem shows that all acceptable programming systems are equivalent to each other in the formal sense of numbering theory. Definition The formalization of computability theory by Kleene led to a particular universal partial computable function Ψ(''e'', ''x'') defined using the T predicate. This function is universal in the sense that it is partial computable, and for any partial computable function ''f'' there is an ''e'' such that, for all ''x'', ''f''(''x'') = Ψ(''e'',''x''), where the equality means that either both sides are undefined or both are defined and are equal. It is common to write ψ''e''(''x'') for Ψ(''e'',''x''); thus the sequence ψ0, ψ1, ... is an enumeration of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Computability Theory
Computability theory, also known as recursion theory, is a branch of mathematical logic, computer science, and the theory of computation that originated in the 1930s with the study of computable functions and Turing degrees. The field has since expanded to include the study of generalized computability and definable set, definability. In these areas, computability theory overlaps with proof theory and effective descriptive set theory. Basic questions addressed by computability theory include: * What does it mean for a function (mathematics), function on the natural numbers to be computable? * How can noncomputable functions be classified into a hierarchy based on their level of noncomputability? Although there is considerable overlap in terms of knowledge and methods, mathematical computability theorists study the theory of relative computability, reducibility notions, and degree structures; those in the computer science field focus on the theory of computational complexity theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Numbering (computability Theory)
There are many different numbering schemes for assigning nominal numbers to entities. These generally require an agreed set of rules, or a central coordinator. The schemes can be considered to be examples of a primary key of a database management system table, whose table definitions require a database design. In computability theory, the simplest numbering scheme is the assignment of natural numbers to a set of objects such as functions, rational numbers, graphs, or words in some formal language. A numbering can be used to transfer the idea of computability and related concepts, which are originally defined on the natural numbers using computable functions, to these different types of objects. A simple extension is to assign cardinal numbers to physical objects according to the choice of some base of reference and of measurement units for counting or measuring these objects within a given precision. In such case, numbering is a kind of classification, i.e. assigning a numeric pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Partial Computable Function
Computable functions are the basic objects of study in computability theory. Informally, a function is ''computable'' if there is an algorithm that computes the value of the function for every value of its argument. Because of the lack of a precise definition of the concept of algorithm, every formal definition of computability must refer to a specific model of computation. Many such models of computation have been proposed, the major ones being Turing machines, register machines, lambda calculus and general recursive functions. Although these four are of a very different nature, they provide exactly the same class of computable functions, and, for every model of computation that has ever been proposed, the computable functions for such a model are computable for the above four models of computation. The Church–Turing thesis is the unprovable assertion that every notion of computability that can be imagined can compute only functions that are computable in the above sense. Befo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Stephen Cole Kleene
Stephen Cole Kleene ( ; January 5, 1909 – January 25, 1994) was an American mathematician. One of the students of Alonzo Church, Kleene, along with Rózsa Péter, Alan Turing, Emil Post, and others, is best known as a founder of the branch of mathematical logic known as recursion theory, which subsequently helped to provide the foundations of theoretical computer science. Kleene's work grounds the study of computable functions. A number of mathematical concepts are named after him: Kleene hierarchy, Kleene algebra, the Kleene star (Kleene closure), Kleene's recursion theorem and the Kleene fixed-point theorem. He also invented regular expressions in 1951 to describe McCulloch-Pitts neural networks, and made significant contributions to the foundations of mathematical intuitionism. Biography Kleene was awarded a bachelor's degree from Amherst College in 1930. He was awarded a Ph.D. in mathematics from Princeton University in 1934, where his thesis, entitled ''A Theory of Po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Kleene's T Predicate
In computability theory, the T predicate, first studied by mathematician Stephen Cole Kleene, is a particular set of triples of natural numbers that is used to represent computable functions within formal theories of arithmetic. Informally, the ''T'' predicate tells whether a particular computer program will halt when run with a particular input, and the corresponding ''U'' function is used to obtain the results of the computation if the program does halt. As with the smn theorem, the original notation used by Kleene has become standard terminology for the concept.The predicate described here was presented in (Kleene 1943) and (Kleene 1952), and this is what is usually called "Kleene's ''T'' predicate". (Kleene 1967) uses the letter ''T'' to describe a different predicate related to computable functions, but which cannot be used to obtain Kleene's normal form theorem. Definition The definition depends on a suitable Gödel numbering that assigns natural numbers to computable ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (often shortened as "iff") is paraphrased by the biconditional, a logical connective between statements. The biconditional is true in two cases, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Smn Theorem
In computability theory the ' theorem, written also as "smn-theorem" or "s-m-n theorem" (also called the translation lemma, parameter theorem, and the parameterization theorem) is a basic result about programming languages (and, more generally, Gödel numberings of the computable functions) (Soare 1987, Rogers 1967). It was first proved by Stephen Cole Kleene (1943). The name ' comes from the occurrence of an ''S'' with subscript ''n'' and superscript ''m'' in the original formulation of the theorem (see below). In practical terms, the theorem says that for a given programming language and positive integers ''m'' and ''n'', there exists a particular algorithm that accepts as input the source code of a program with free variables, together with ''m'' values. This algorithm generates source code that effectively substitutes the values for the first ''m'' free variables, leaving the rest of the variables free. The smn-theorem states that given a function of two arguments g(x,y) wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hartley Rogers, Jr
Hartley Rogers Jr. (July 6, 1926 – July 17, 2015) was an American mathematician who worked in computability theory, and was a professor in the Mathematics Department of the Massachusetts Institute of Technology. Biography Born in 1926 in Buffalo, New York, Rogers studied English as an undergraduate at Yale University, graduating in 1946. After visiting the University of Cambridge under a Henry Fellowship, he returned to Yale for a master's degree in physics, which he completed in 1950. He studied mathematics under Alonzo Church at Princeton, earned a second master's degree in 1951, and received his Ph.D. there in 1952. He was a Benjamin Peirce Lecturer at Harvard University from 1952 to 1955. After holding a visiting position at MIT, he became a professor in the MIT Mathematics Department in 1956. His doctoral students included Patrick Fischer, Louis Hodes, Carl Jockusch, Andrew Kahr, David Luckham, Rohit Parikh, David Park, and John Stillwell. He chaired the MIT faculty ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bijection
In mathematics, a bijection, bijective function, or one-to-one correspondence is a function between two sets such that each element of the second set (the codomain) is the image of exactly one element of the first set (the domain). Equivalently, a bijection is a relation between two sets such that each element of either set is paired with exactly one element of the other set. A function is bijective if it is invertible; that is, a function f:X\to Y is bijective if and only if there is a function g:Y\to X, the ''inverse'' of , such that each of the two ways for composing the two functions produces an identity function: g(f(x)) = x for each x in X and f(g(y)) = y for each y in Y. For example, the ''multiplication by two'' defines a bijection from the integers to the even numbers, which has the ''division by two'' as its inverse function. A function is bijective if and only if it is both injective (or ''one-to-one'')—meaning that each element in the codomain is mappe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Friedberg Numbering
In computability theory, a Friedberg numbering is a numbering There are many different numbering schemes for assigning nominal numbers to entities. These generally require an agreed set of rules, or a central coordinator. The schemes can be considered to be examples of a primary key In the relational model ... (enumeration) of the set of all uniformly recursively enumerable sets that has no repetitions: each recursively enumerable set appears exactly once in the enumeration (Vereščagin and Shen 2003:30). The existence of such numberings was established by Richard M. Friedberg in 1958 (Cutland 1980:78). References * Nigel Cutland (1980), ''Computability: An Introduction to Recursive Function Theory'', Cambridge University Press. . * Richard M. Friedberg (1958), ''Three Theorems on Recursive Enumeration. I. Decomposition. II. Maximal Set. III. Enumeration Without Duplication'', ''Journal of Symbolic Logic'' 23:3, pp. 309–316. * Nikolaj K. Vereščagin and A. Shen (200 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Yury Yershov
Yury Leonidovich Yershov (, born 1 May 194 is a Soviet and Russian mathematician. Yury Yershov was born in 1940 in Novosibirsk. In 1958 he entered the Tomsk State University and in 1963 graduated from the Mathematical Department of the Novosibirsk State University. In 1964 he successfully defended his PhD thesis "Decidable and Undecidable Theories" (advisor Anatoly Maltsev). In 1966 he successfully defended his DrSc thesis "Elementary Theory of Fields" (Элементарные теория полей). Apart from being a mathematician, Yershov was a member of the Communist Party and had different distinguished administrative duties in Novosibirsk State University. Yershov has been accused of antisemitic practices, and his visit to the U.S. in 1980 drew public protests by a number of U.S. mathematicians. Yershov himself denied the validity of these accusations. Yury Yershov is a member of the Russian Academy of Sciences, professor emeritus of Novosibirsk State University and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Robert I
Robert I may refer to: * Robert I, Duke of Neustria (697–748) *Robert I of France (866–923), King of France, 922–923, rebelled against Charles the Simple * Rollo, Duke of Normandy (c. 846 – c. 930; reigned 911–927) * Robert I Archbishop of Rouen (d. 1037), Archbishop of Rouen, 989–1037, son of Duke Richard I of Normandy * Robert the Magnificent (1000–1035), also named Robert I, Duke of Normandy, 1027–1035), father of William the Conqueror. Sometimes known as Robert II, with Rollo of Normandy, c. 860 – c. 932, as Robert I because Robert was his baptismal name when he became a Christian * Robert I, Duke of Burgundy (1011–1076), Duke of Burgundy, 1032–1076 * Robert I, Count of Flanders (1029–1093), also named Robert the Frisian, Count of Flanders, 1071–1093 * Robert I de Brus (ca. 1078 – 1141/1142) * Robert I of Dreux (c. 1123 – 1188), Count of Braine in France, son of King Louis VI *Robert I of Artois (1216–1250), son of King Louis VIII of France *Ro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |