|
Aczel's Anti-foundation Axiom
In the foundations of mathematics, Aczel's anti-foundation axiom is an axiom set forth by , as an alternative to the axiom of foundation in Zermelo–Fraenkel set theory. It states that every accessible pointed directed graph corresponds to exactly one set. In particular, according to this axiom, the graph consisting of a single vertex with a loop corresponds to a set that contains only itself as element, i.e. a Quine atom. A set theory obeying this axiom is necessarily a non-well-founded set theory. Accessible pointed graphs An accessible pointed graph is a directed graph with a distinguished vertex (the "root") such that for any node in the graph there is at least one path in the directed graph from the root to that node. The anti-foundation axiom postulates that each such directed graph corresponds to the membership structure of exactly one set. For example, the directed graph with only one node and an edge from that node to itself corresponds to a set of the form ''x'' = . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Foundations Of Mathematics
Foundations of mathematics is the study of the philosophy, philosophical and logical and/or algorithmic basis of mathematics, or, in a broader sense, the mathematical investigation of what underlies the philosophical theories concerning the nature of mathematics. In this latter sense, the distinction between foundations of mathematics and philosophy of mathematics turns out to be quite vague. Foundations of mathematics can be conceived as the study of the basic mathematical concepts (set, function, geometrical figure, number, etc.) and how they form hierarchies of more complex structures and concepts, especially the fundamentally important structures that form the language of mathematics (formulas, theories and their model theory, models giving a meaning to formulas, definitions, proofs, algorithms, etc.) also called metamathematics, metamathematical concepts, with an eye to the philosophical aspects and the unity of mathematics. The search for foundations of mathematics is a cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy or fit' or 'that which commends itself as evident'. The term has subtle differences in definition when used in the context of different fields of study. As defined in classic philosophy, an axiom is a statement that is so evident or well-established, that it is accepted without controversy or question. As used in modern logic, an axiom is a premise or starting point for reasoning. As used in mathematics, the term ''axiom'' is used in two related but distinguishable senses: "logical axioms" and "non-logical axioms". Logical axioms are usually statements that are taken to be true within the system of logic they define and are often shown in symbolic form (e.g., (''A'' and ''B'') implies ''A''), while non-logical axioms (e.g., ) are actually ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiom Of Foundation
In mathematics, the axiom of regularity (also known as the axiom of foundation) is an axiom of Zermelo–Fraenkel set theory that states that every non-empty set ''A'' contains an element that is disjoint from ''A''. In first-order logic, the axiom reads: : \forall x\,(x \neq \varnothing \rightarrow \exists y(y \in x\ \land y \cap x = \varnothing)). The axiom of regularity together with the axiom of pairing implies that no set is an element of itself, and that there is no infinite sequence (''an'') such that ''ai+1'' is an element of ''ai'' for all ''i''. With the axiom of dependent choice (which is a weakened form of the axiom of choice), this result can be reversed: if there are no such infinite sequences, then the axiom of regularity is true. Hence, in this context the axiom of regularity is equivalent to the sentence that there are no downward infinite membership chains. The axiom was introduced by ; it was adopted in a formulation closer to the one found in contemporary tex ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Zermelo–Fraenkel Set Theory
In set theory, Zermelo–Fraenkel set theory, named after mathematicians Ernst Zermelo and Abraham Fraenkel, is an axiomatic system that was proposed in the early twentieth century in order to formulate a theory of sets free of paradoxes such as Russell's paradox. Today, Zermelo–Fraenkel set theory, with the historically controversial axiom of choice (AC) included, is the standard form of axiomatic set theory and as such is the most common foundation of mathematics. Zermelo–Fraenkel set theory with the axiom of choice included is abbreviated ZFC, where C stands for "choice", and ZF refers to the axioms of Zermelo–Fraenkel set theory with the axiom of choice excluded. Informally, Zermelo–Fraenkel set theory is intended to formalize a single primitive notion, that of a hereditary well-founded set, so that all entities in the universe of discourse are such sets. Thus the axioms of Zermelo–Fraenkel set theory refer only to pure sets and prevent its models from containing u ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Accessible Pointed Graph
In mathematics, and, in particular, in graph theory, a rooted graph is a graph in which one vertex has been distinguished as the root. Both directed and undirected versions of rooted graphs have been studied, and there are also variant definitions that allow multiple roots. Rooted graphs may also be known (depending on their application) as pointed graphs or flow graphs. In some of the applications of these graphs, there is an additional requirement that the whole graph be reachable from the root vertex. Variations In topological graph theory, the notion of a rooted graph may be extended to consider multiple vertices or multiple edges as roots. The former are sometimes called vertex-rooted graphs in order to distinguish them from edge-rooted graphs in this context. Graphs with multiple nodes designated as roots are also of some interest in combinatorics, in the area of random graphs. These graphs are also called multiply rooted graphs. The terms rooted directed graph or roote ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Set (mathematics)
A set is the mathematical model for a collection of different things; a set contains '' elements'' or ''members'', which can be mathematical objects of any kind: numbers, symbols, points in space, lines, other geometrical shapes, variables, or even other sets. The set with no element is the empty set; a set with a single element is a singleton. A set may have a finite number of elements or be an infinite set. Two sets are equal if they have precisely the same elements. Sets are ubiquitous in modern mathematics. Indeed, set theory, more specifically Zermelo–Fraenkel set theory, has been the standard way to provide rigorous foundations for all branches of mathematics since the first half of the 20th century. History The concept of a set emerged in mathematics at the end of the 19th century. The German word for set, ''Menge'', was coined by Bernard Bolzano in his work ''Paradoxes of the Infinite''. Georg Cantor, one of the founders of set theory, gave the following defin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quine Atom
In set theory, a branch of mathematics, an urelement or ur-element (from the German prefix ''ur-'', 'primordial') is an object that is not a set, but that may be an element of a set. It is also referred to as an atom or individual. Theory There are several different but essentially equivalent ways to treat urelements in a first-order theory. One way is to work in a first-order theory with two sorts, sets and urelements, with ''a'' ∈ ''b'' only defined when ''b'' is a set. In this case, if ''U'' is an urelement, it makes no sense to say X \in U, although U \in X is perfectly legitimate. Another way is to work in a one-sorted theory with a unary relation used to distinguish sets and urelements. As non-empty sets contain members while urelements do not, the unary relation is only needed to distinguish the empty set from urelements. Note that in this case, the axiom of extensionality must be formulated to apply only to objects that are not urelements. This situation is analogo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Non-well-founded Set Theory
Non-well-founded set theories are variants of axiomatic set theory that allow sets to be elements of themselves and otherwise violate the rule of well-foundedness. In non-well-founded set theories, the foundation axiom of ZFC is replaced by axioms implying its negation. The study of non-well-founded sets was initiated by Dmitry Mirimanoff in a series of papers between 1917 and 1920, in which he formulated the distinction between well-founded and non-well-founded sets; he did not regard well-foundedness as an axiom. Although a number of axiomatic systems of non-well-founded sets were proposed afterwards, they did not find much in the way of applications until Peter Aczel’s hyperset theory in 1988. The theory of non-well-founded sets has been applied in the logical modelling of non-terminating computational processes in computer science (process algebra and final semantics), linguistics and natural language semantics (situation theory), philosophy (work on the Liar Paradox), an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Directed Graph
In mathematics, and more specifically in graph theory, a directed graph (or digraph) is a graph that is made up of a set of vertices connected by directed edges, often called arcs. Definition In formal terms, a directed graph is an ordered pair where * ''V'' is a set whose elements are called '' vertices'', ''nodes'', or ''points''; * ''A'' is a set of ordered pairs of vertices, called ''arcs'', ''directed edges'' (sometimes simply ''edges'' with the corresponding set named ''E'' instead of ''A''), ''arrows'', or ''directed lines''. It differs from an ordinary or undirected graph, in that the latter is defined in terms of unordered pairs of vertices, which are usually called ''edges'', ''links'' or ''lines''. The aforementioned definition does not allow a directed graph to have multiple arrows with the same source and target nodes, but some authors consider a broader definition that allows directed graphs to have such multiple arcs (namely, they allow the arc set to be a m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vertex (graph Theory)
In discrete mathematics, and more specifically in graph theory, a vertex (plural vertices) or node is the fundamental unit of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges (unordered pairs of vertices), while a directed graph consists of a set of vertices and a set of arcs (ordered pairs of vertices). In a diagram of a graph, a vertex is usually represented by a circle with a label, and an edge is represented by a line or arrow extending from one vertex to another. From the point of view of graph theory, vertices are treated as featureless and indivisible objects, although they may have additional structure depending on the application from which the graph arises; for instance, a semantic network is a graph in which the vertices represent concepts or classes of objects. The two vertices forming an edge are said to be the endpoints of this edge, and the edge is said to be incident to the vertices. A vertex ''w'' is said to be ad ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Path (graph Theory)
In graph theory, a path in a graph is a finite or infinite sequence of edges which joins a sequence of vertices which, by most definitions, are all distinct (and since the vertices are distinct, so are the edges). A directed path (sometimes called dipathGraph Structure Theory: Proceedings of the AMS-IMS-SIAM Joint Summer Research Conference on Graph Minors, Held June 22 to July 5, 1991p.205/ref>) in a directed graph is a finite or infinite sequence of edges which joins a sequence of distinct vertices, but with the added restriction that the edges be all directed in the same direction. Paths are fundamental concepts of graph theory, described in the introductory sections of most graph theory texts. See e.g. Bondy and Murty (1976), Gibbons (1985), or Diestel (2005). Korte et al. (1990) cover more advanced algorithmic topics concerning paths in graphs. Definitions Walk, trail, and path * A walk is a finite or infinite sequence of edges which joins a sequence of vertices. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
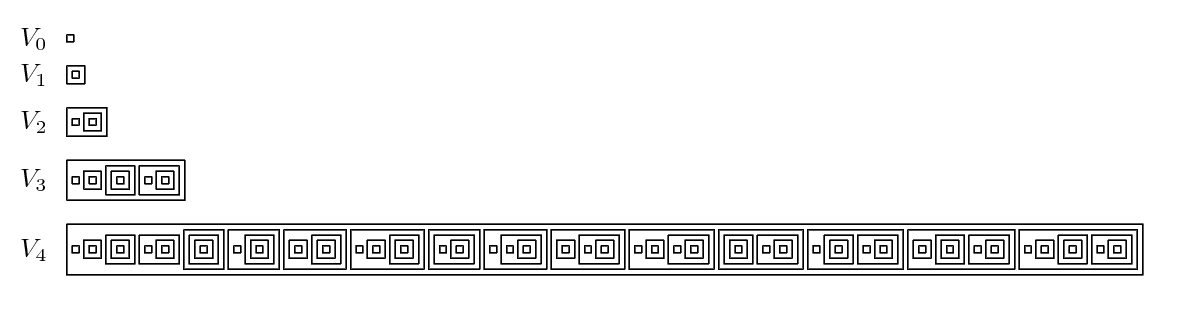
Von Neumann Universe
In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930. The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''Vα'', called the cumulative hierarchy, based on their rank. Definition The cumulative hierarchy is a collection of sets ''V''α indexed by the class of ordinal numbers; in particular, ''V''α is the set of all sets having ranks less than α. Thus there is one set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |