|
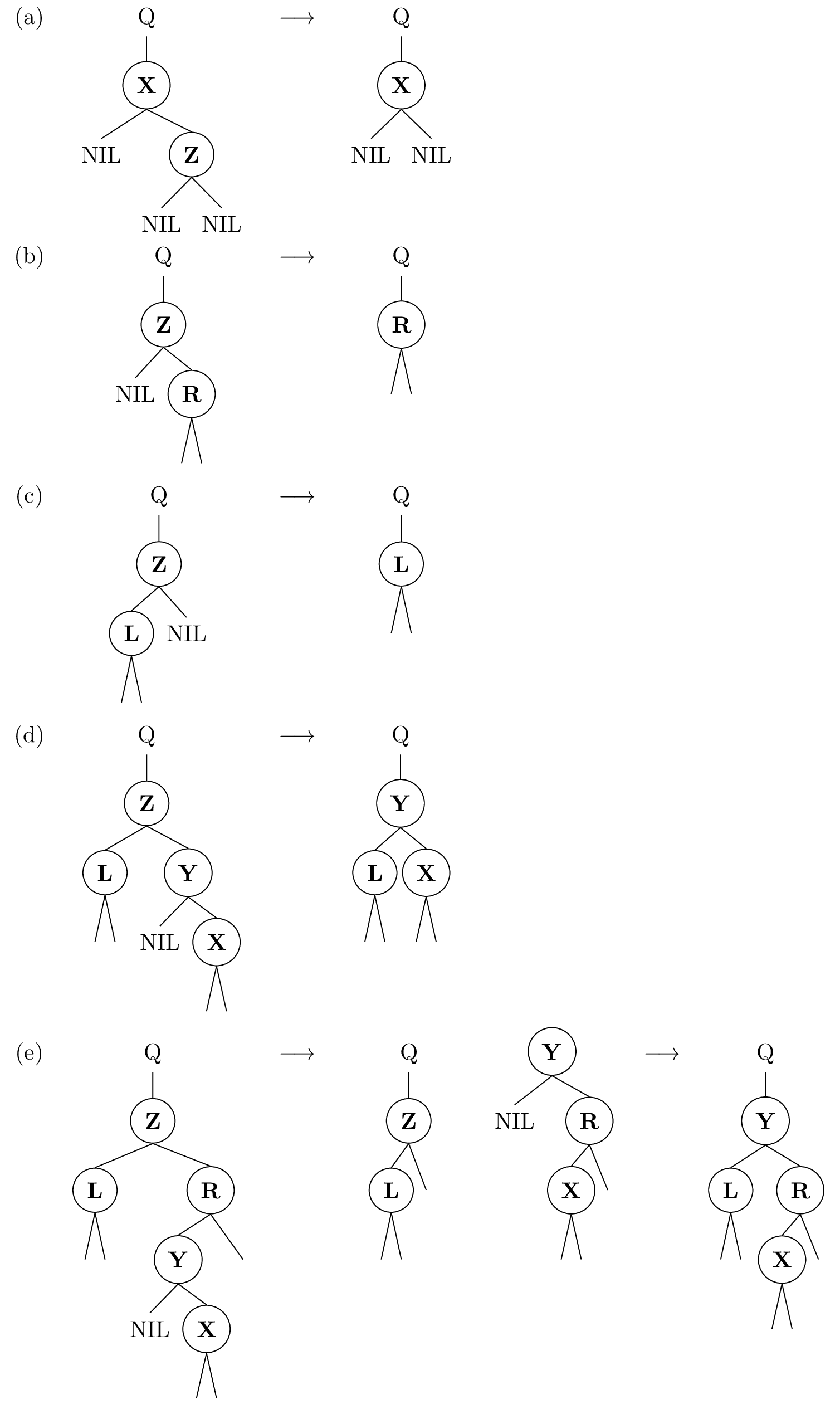
AVL Trees
In computer science, an AVL tree (named after inventors Adelson-Velsky and Landis) is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Lookup, insertion, and deletion all take time in both the average and worst cases, where n is the number of nodes in the tree prior to the operation. Insertions and deletions may require the tree to be rebalanced by one or more tree rotations. The AVL tree is named after its two Soviet inventors, Georgy Adelson-Velsky and Evgenii Landis, who published it in their 1962 paper "An algorithm for the organization of information". It is the first self-balancing binary search tree data structure to be invented. AVL trees are often compared with red–black trees because both support the same set of operations and take \text(\log n) time for the basic operations. For lookup-intensive ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Tree (data Structure)
In computer science, a tree is a widely used abstract data type that represents a hierarchical tree structure with a set of connected nodes. Each node in the tree can be connected to many children (depending on the type of tree), but must be connected to exactly one parent, except for the ''root'' node, which has no parent (i.e., the root node as the top-most node in the tree hierarchy). These constraints mean there are no cycles or "loops" (no node can be its own ancestor), and also that each child can be treated like the root node of its own subtree, making recursion a useful technique for tree traversal. In contrast to linear data structures, many trees cannot be represented by relationships between neighboring nodes (parent and children nodes of a node under consideration, if they exist) in a single straight line (called edge or link between two adjacent nodes). Binary trees are a commonly used type, which constrain the number of children for each parent to at most two. Whe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
WAVL Tree
In computer science, a WAVL tree or weak AVL tree is a self-balancing binary search tree. WAVL trees are named after AVL trees, another type of balanced search tree, and are closely related both to AVL trees and red–black trees, which all fall into a common framework of rank balanced trees. Like other balanced binary search trees, WAVL trees can handle insertion, deletion, and search operations in time per operation.. WAVL trees are designed to combine some of the best properties of both AVL trees and red–black trees. One advantage of AVL trees over red–black trees is being more balanced: they have height at most \log_ n\approx 1.44\log_2 n (for a tree with data items, where \varphi is the golden ratio), while red–black trees have larger maximum height, 2\log_2 n. If a WAVL tree is created using only insertions, without deletions, then it has the same small height bound that an AVL tree has. On the other hand, red–black trees have the advantage over AVL trees in lesser ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Union (set Theory)
In set theory, the union (denoted by ∪) of a collection of Set (mathematics), sets is the set of all element (set theory), elements in the collection. It is one of the fundamental operations through which sets can be combined and related to each other. A refers to a union of Zero, zero () sets and it is by definition equal to the empty set. For explanation of the symbols used in this article, refer to the List of mathematical symbols, table of mathematical symbols. Binary union The union of two sets ''A'' and ''B'' is the set of elements which are in ''A'', in ''B'', or in both ''A'' and ''B''. In set-builder notation, : A \cup B = \. For example, if ''A'' = and ''B'' = then ''A'' ∪ ''B'' = . A more elaborate example (involving two infinite sets) is: : ''A'' = : ''B'' = : A \cup B = \ As another example, the number 9 is ''not'' contained in the union of the set of prime numbers and the set of even numbers , because 9 is neither prime nor even. Sets cannot ha ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Loop Invariant
In computer science, a loop invariant is a property of a program loop that is true before (and after) each iteration. It is a logical assertion, sometimes checked with a code assertion. Knowing its invariant(s) is essential in understanding the effect of a loop. In formal program verification, particularly the Floyd-Hoare approach, loop invariants are expressed by formal predicate logic and used to prove properties of loops and by extension algorithms that employ loops (usually correctness properties). The loop invariants will be true on entry into a loop and following each iteration, so that on exit from the loop both the loop invariants and the loop termination condition can be guaranteed. From a programming methodology viewpoint, the loop invariant can be viewed as a more abstract specification of the loop, which characterizes the deeper purpose of the loop beyond the details of this implementation. A survey article covers fundamental algorithms from many areas of compu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Rebalancing
In finance and investing, rebalancing of investments (or constant mix) is a strategy of bringing a portfolio that has deviated away from one's target asset allocation back into line. This can be implemented by transferring assets, that is, selling investments of an asset class that is overweight and using the money to buy investments in a class that is underweight, but it also applies to adding or removing money from a portfolio, that is, putting new money into an underweight class, or making withdrawals from an overweight class. History Now a commonplace strategy, rebalancing can be traced back to the 1940s and was pioneered by Sir John Templeton, among others. Templeton used an early version of the cyclically adjusted price-to-earnings ratio to estimate valuations for the overall U.S. stock market. Based on the theory that high stock valuations led to lower expected return on investment over the next few years, Templeton allocated a greater percentage of a portfolio to stocks w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Balance Factor
Balance may refer to: Common meanings * Balance (ability) in biomechanics * Balance (accounting) * Balance or weighing scale * Balance, as in equality (mathematics) or equilibrium Arts and entertainment Film * ''Balance'' (1983 film), a Bulgarian film * ''Balance'' (1989 film), a short animated film * '' La Balance'', a 1982 French film Television * '' Balance: Television for Living Well'', a Canadian television talk show * "The Balance" (Roswell), an episode of the television series ''Roswell'' * "The Balance", an episode of the animated series ''Justice League Unlimited'' Music Performers * Balance (band), a 1980s pop-rock group Albums * ''Balance'' (Akrobatik album), 2003 * ''Balance'' (Kim-Lian album), 2004 * ''Balance'' (Leo Kottke album), 1978 * ''Balance'' (Masta Killa album), 2025 * ''Balance'' (Joe Morris album), 2014 * ''Balance'' (Swollen Members album), 1999 * ''Balance'' (Ty Tabor album), 2008 * ''Balance'' (Melly Goeslaw album), 2013 * ''Balance'' (Van ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Search Tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a Rooted tree, rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is Time complexity#Linear time, linear with respect to the height of the tree. Binary search trees allow Binary search algorithm, binary search for fast lookup, addition, and removal of data items. Since the nodes in a BST are laid out so that each comparison skips about half of the remaining tree, the lookup performance is proportional to that of binary logarithm. BSTs were devised in the 1960s for the problem of efficient storage of labeled data and are attributed to Conway Berners-Lee and David_Wheeler_(computer_scientist), David Wheeler. The performance of a binary search tree is dependent on the order of insertion of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Amortized Complexity
In computer science, amortized analysis is a method for analyzing a given algorithm's complexity, or how much of a resource, especially time or memory, it takes to execute. The motivation for amortized analysis is that looking at the worst-case run time can be too pessimistic. Instead, amortized analysis averages the running times of operations in a sequence over that sequence. As a conclusion: "Amortized analysis is a useful tool that complements other techniques such as worst-case and average-case analysis." For a given operation of an algorithm, certain situations (e.g., input parametrizations or data structure contents) may imply a significant cost in resources, whereas other situations may not be as costly. The amortized analysis considers both the costly and less costly operations together over the whole sequence of operations. This may include accounting for different types of input, length of the input, and other factors that affect its performance. History Amortize ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Weak Ordering
In mathematics, especially order theory, a weak ordering is a mathematical formalization of the intuitive notion of a ranking of a set (mathematics), set, some of whose members may be Tie (draw), tied with each other. Weak orders are a generalization of totally ordered sets (rankings without ties) and are in turn generalized by (strictly) partially ordered sets and preorders.. There are several common ways of formalizing weak orderings, that are different from each other but Cryptomorphism, cryptomorphic (interconvertable with no loss of information): they may be axiomatized as strict weak orderings (strictly partially ordered sets in which incomparability is a transitive relation), as total preorders (transitive binary relations in which at least one of the two possible relations exists between every pair of elements), or as ordered partitions (partition of a set, partitions of the elements into disjoint subsets, together with a total order on the subsets). In many cases anot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Total Order
In mathematics, a total order or linear order is a partial order in which any two elements are comparable. That is, a total order is a binary relation \leq on some set X, which satisfies the following for all a, b and c in X: # a \leq a ( reflexive). # If a \leq b and b \leq c then a \leq c ( transitive). # If a \leq b and b \leq a then a = b ( antisymmetric). # a \leq b or b \leq a ( strongly connected, formerly called totality). Requirements 1. to 3. just make up the definition of a partial order. Reflexivity (1.) already follows from strong connectedness (4.), but is required explicitly by many authors nevertheless, to indicate the kinship to partial orders. Total orders are sometimes also called simple, connex, or full orders. A set equipped with a total order is a totally ordered set; the terms simply ordered set, linearly ordered set, toset and loset are also used. The term ''chain'' is sometimes defined as a synonym of ''totally ordered set'', but generally refers to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Binary Search Tree
In computer science, a binary search tree (BST), also called an ordered or sorted binary tree, is a Rooted tree, rooted binary tree data structure with the key of each internal node being greater than all the keys in the respective node's left subtree and less than the ones in its right subtree. The time complexity of operations on the binary search tree is Time complexity#Linear time, linear with respect to the height of the tree. Binary search trees allow Binary search algorithm, binary search for fast lookup, addition, and removal of data items. Since the nodes in a BST are laid out so that each comparison skips about half of the remaining tree, the lookup performance is proportional to that of binary logarithm. BSTs were devised in the 1960s for the problem of efficient storage of labeled data and are attributed to Conway Berners-Lee and David_Wheeler_(computer_scientist), David Wheeler. The performance of a binary search tree is dependent on the order of insertion of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |