|
ATS (programming Language)
In computing, ATS (Applied Type System) is a multi-paradigm, general-purpose, high-level, functional programming language. It is a dialect of the programming language ML, designed by Hongwei Xi to unify computer programming with formal specification. ATS has support for combining theorem proving with practical programming through the use of advanced type systems. A past version of The Computer Language Benchmarks Game has demonstrated that the performance of ATS is comparable to that of the languages C and C++. By using theorem proving and strict type checking, the compiler can detect and prove that its implemented functions are not susceptible to bugs such as division by zero, memory leaks, buffer overflow, and other forms of memory corruption by verifying pointer arithmetic and reference counting before the program runs. Also, by using the integrated theorem-proving system of ATS (ATS/LF), the programmer may make use of static constructs that are intertwined with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Comparison Of Multi-paradigm Programming Languages
Programming languages can be grouped by the number and types of paradigms supported. Paradigm summaries A concise reference for the programming paradigms listed in this article. * Concurrent programming – have language constructs for concurrency, these may involve multi-threading, support for distributed computing, message passing, shared resources (including shared memory), or futures ** Actor programming – concurrent computation with ''actors'' that make local decisions in response to the environment (capable of selfish or competitive behaviour) * Constraint programming – relations between variables are expressed as constraints (or constraint networks), directing allowable solutions (uses constraint satisfaction or simplex algorithm) * Dataflow programming – forced recalculation of formulas when data values change (e.g. spreadsheets) * Declarative programming – describes what computation should perform, without specifying detailed state changes cf. imperative pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dialect (computing)
A programming language is a system of notation for writing computer programs. Programming languages are described in terms of their syntax (form) and semantics (meaning), usually defined by a formal language. Languages usually provide features such as a type system, variables, and mechanisms for error handling. An implementation of a programming language is required in order to execute programs, namely an interpreter or a compiler. An interpreter directly executes the source code, while a compiler produces an executable program. Computer architecture has strongly influenced the design of programming languages, with the most common type ( imperative languages—which implement operations in a specified order) developed to perform well on the popular von Neumann architecture. While early programming languages were closely tied to the hardware, over time they have developed more abstraction to hide implementation details for greater simplicity. Thousands of programming lang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Programming Paradigm
A programming paradigm is a relatively high-level way to conceptualize and structure the implementation of a computer program. A programming language can be classified as supporting one or more paradigms. Paradigms are separated along and described by different dimensions of programming. Some paradigms are about implications of the execution model, such as allowing Side effect (computer science), side effects, or whether the sequence of operations is defined by the execution model. Other paradigms are about the way code is organized, such as grouping into units that include both state and behavior. Yet others are about Syntax (programming languages), syntax and Formal grammar, grammar. Some common programming paradigms include (shown in hierarchical relationship): * imperative programming, Imperative code directly controls Control flow, execution flow and state change, explicit statements that change a program state ** procedural programming, procedural organized as function (c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reference Counting
In computer science, reference counting is a programming technique of storing the number of references, pointers, or handles to a resource, such as an object, a block of memory, disk space, and others. In garbage collection algorithms, reference counts may be used to deallocate objects that are no longer needed. Advantages and disadvantages The main advantage of the reference counting over tracing garbage collection is that objects are reclaimed ''as soon as'' they can no longer be referenced, and in an incremental fashion, without long pauses for collection cycles and with clearly defined lifetime of every object. In real-time applications or systems with limited memory, this is important to maintain responsiveness. Reference counting is also among the simplest forms of memory management to implement. It also allows for effective management of non-memory resources such as operating system objects, which are often much scarcer than memory (tracing garbage collection systems ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pointer Arithmetic
In computer science, a pointer is an object in many programming languages that stores a memory address. This can be that of another value located in computer memory, or in some cases, that of memory-mapped computer hardware. A pointer ''references'' a location in memory, and obtaining the value stored at that location is known as ''dereferencing'' the pointer. As an analogy, a page number in a book's index could be considered a pointer to the corresponding page; dereferencing such a pointer would be done by flipping to the page with the given page number and reading the text found on that page. The actual format and content of a pointer variable is dependent on the underlying computer architecture. Using pointers significantly improves performance for repetitive operations, like traversing iterable data structures (e.g. strings, lookup tables, control tables, linked lists, and tree structures). In particular, it is often much cheaper in time and space to copy and derefere ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memory Corruption
Memory corruption occurs in a computer program when the contents of a memory location are modified due to programmatic behavior that exceeds the intention of the original programmer or program/language constructs; this is termed as violation of memory safety. The most likely causes of memory corruption are programming errors (software bugs). When the corrupted memory contents are used later in that program, it leads either to program crash or to strange and bizarre program behavior. Nearly 10% of application crashes on Windows systems are due to heap corruption.{{Cite web, last=Radich, first=Q., last2=Sherer, first2=T., last3=Sharkey, first3=K., last4=Batchelor, first4=D., last5=Kennedy, first5=J. T., last6=Mabee, first6=D., last7=Coulter, first7=D., last8=Michael, first8=S., date=28 April 2021, title=Application Verifier (Windows 7 and Windows Server 2008 R2 Application Quality Cookbook) - Win32 apps, publisher=Microsoft Developer Network, url=https://docs.microsoft.com/en-us/wi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Memory Leak
In computer science, a memory leak is a type of resource leak that occurs when a computer program incorrectly manages memory allocations in a way that memory which is no longer needed is not released. A memory leak may also happen when an object is stored in memory but cannot be accessed by the running code (i.e. unreachable memory). A memory leak has symptoms similar to a number of other problems and generally can only be diagnosed by a programmer with access to the program's source code. A related concept is the "space leak", which is when a program consumes excessive memory but does eventually release it. Because they can exhaust available system memory as an application runs, memory leaks are often the cause of or a contributing factor to software aging. Effects Minor leaks If a program has a memory leak and its memory usage is steadily increasing, there will not usually be an immediate symptom. In modern operating systems, normal memory used by an application is releas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Division By Zero
In mathematics, division by zero, division (mathematics), division where the divisor (denominator) is 0, zero, is a unique and problematic special case. Using fraction notation, the general example can be written as \tfrac a0, where a is the dividend (numerator). The usual definition of the quotient in elementary arithmetic is the number which yields the dividend when multiplication, multiplied by the divisor. That is, c = \tfrac ab is equivalent to c \cdot b = a. By this definition, the quotient q = \tfrac is nonsensical, as the product q \cdot 0 is always 0 rather than some other number a. Following the ordinary rules of elementary algebra while allowing division by zero can create a mathematical fallacy, a subtle mistake leading to absurd results. To prevent this, the arithmetic of real numbers and more general numerical structures called field (mathematics), fields leaves division by zero undefined (mathematics), undefined, and situations where division by zero might occur m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
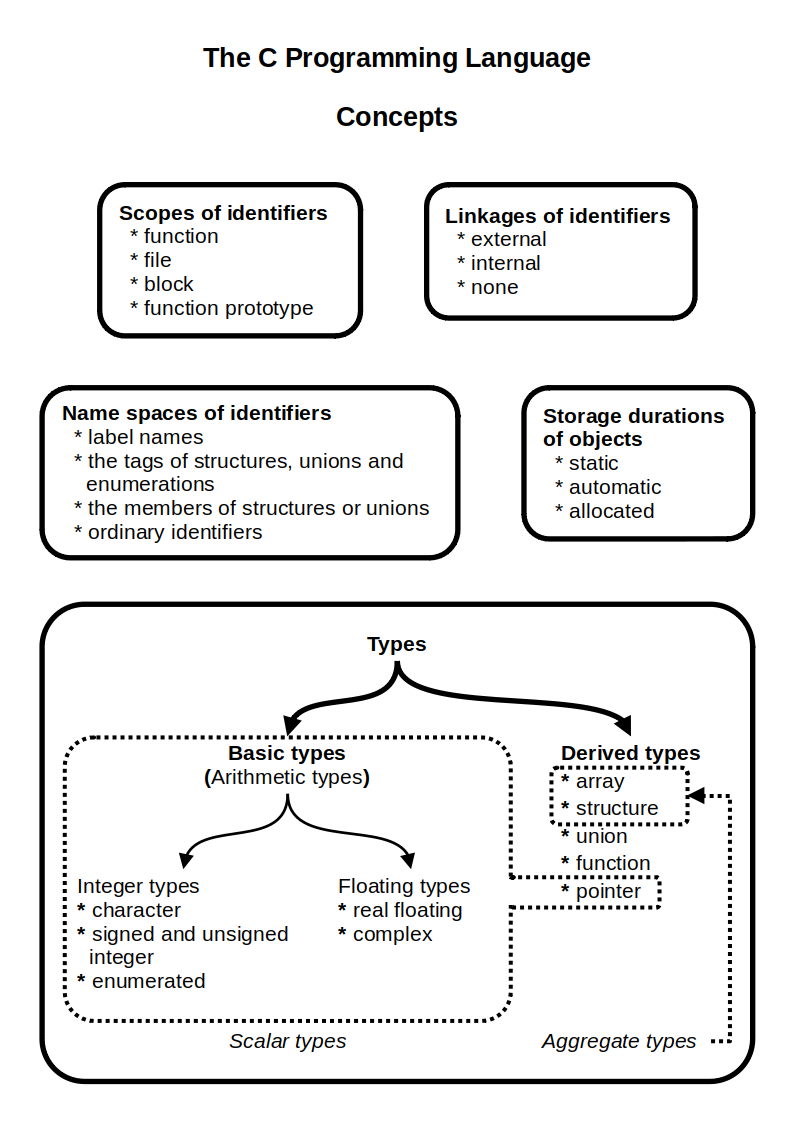
C (programming Language)
C (''pronounced'' '' – like the letter c'') is a general-purpose programming language. It was created in the 1970s by Dennis Ritchie and remains very widely used and influential. By design, C's features cleanly reflect the capabilities of the targeted Central processing unit, CPUs. It has found lasting use in operating systems code (especially in Kernel (operating system), kernels), device drivers, and protocol stacks, but its use in application software has been decreasing. C is commonly used on computer architectures that range from the largest supercomputers to the smallest microcontrollers and embedded systems. A successor to the programming language B (programming language), B, C was originally developed at Bell Labs by Ritchie between 1972 and 1973 to construct utilities running on Unix. It was applied to re-implementing the kernel of the Unix operating system. During the 1980s, C gradually gained popularity. It has become one of the most widely used programming langu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
The Computer Language Benchmarks Game
The Computer Language Benchmarks Game (formerly called The Great Computer Language Shootout) is a free software project for comparing how a given subset of simple algorithms In mathematics and computer science, an algorithm () is a finite sequence of mathematically rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for per ... can be implemented in various popular programming languages. The project consists of: * A set of very simple algorithmic problems (thirteen in total) * Various implementations to the above problems in various programming languages * A set of unit tests to verify that the submitted implementations solve the problem statement * A framework for running and timing the implementations * A website to facilitate the interactive comparison of the results Supported languages Metrics The following aspects of each given implementation are measured: * overall user runt ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Type System
In computer programming, a type system is a logical system comprising a set of rules that assigns a property called a ''type'' (for example, integer, floating point, string) to every '' term'' (a word, phrase, or other set of symbols). Usually the terms are various language constructs of a computer program, such as variables, expressions, functions, or modules. A type system dictates the operations that can be performed on a term. For variables, the type system determines the allowed values of that term. Type systems formalize and enforce the otherwise implicit categories the programmer uses for algebraic data types, data structures, or other data types, such as "string", "array of float", "function returning boolean". Type systems are often specified as part of programming languages and built into interpreters and compilers, although the type system of a language can be extended by optional tools that perform added checks using the language's original type synta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |