|
Axial Multipole Moments
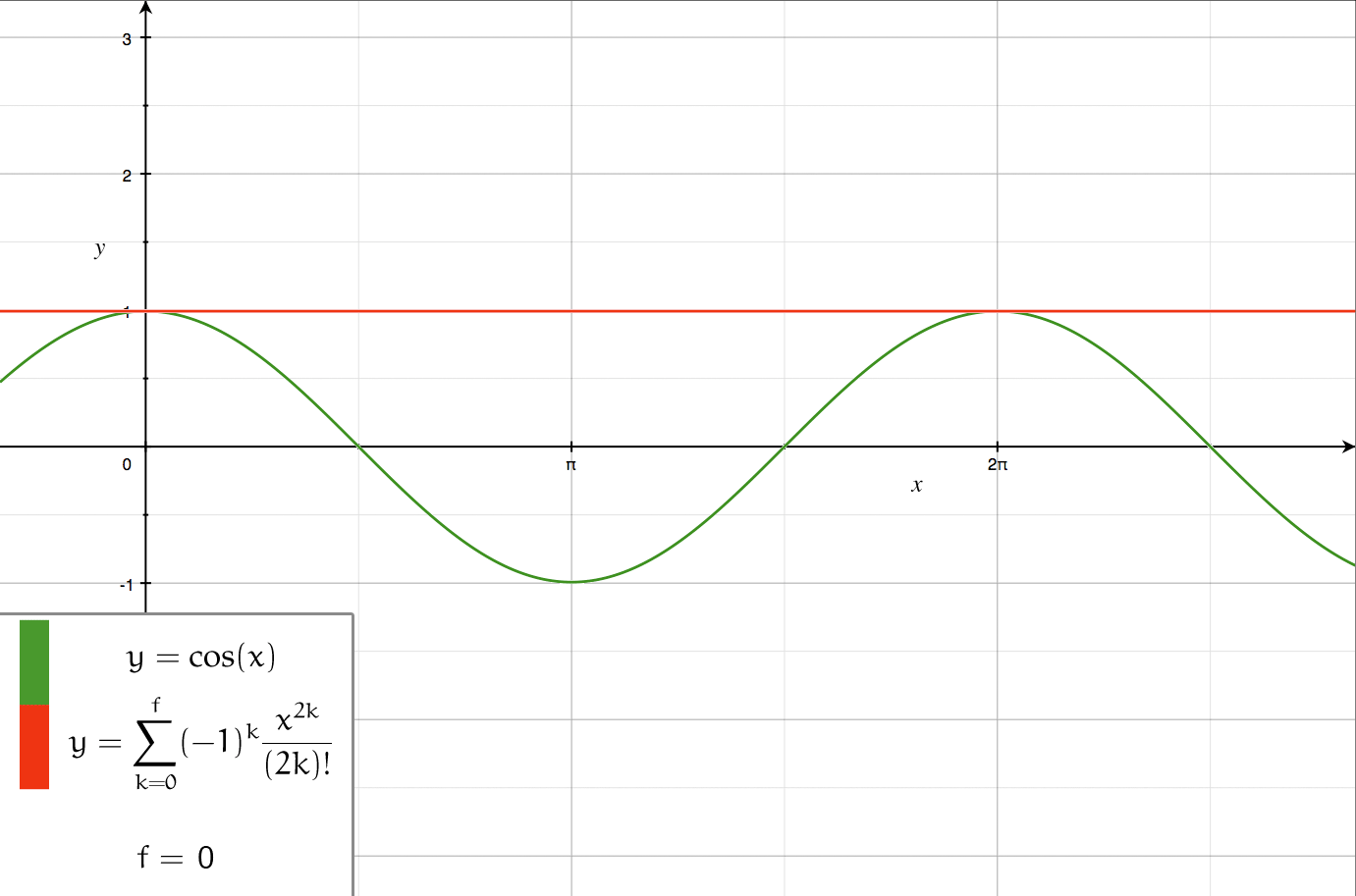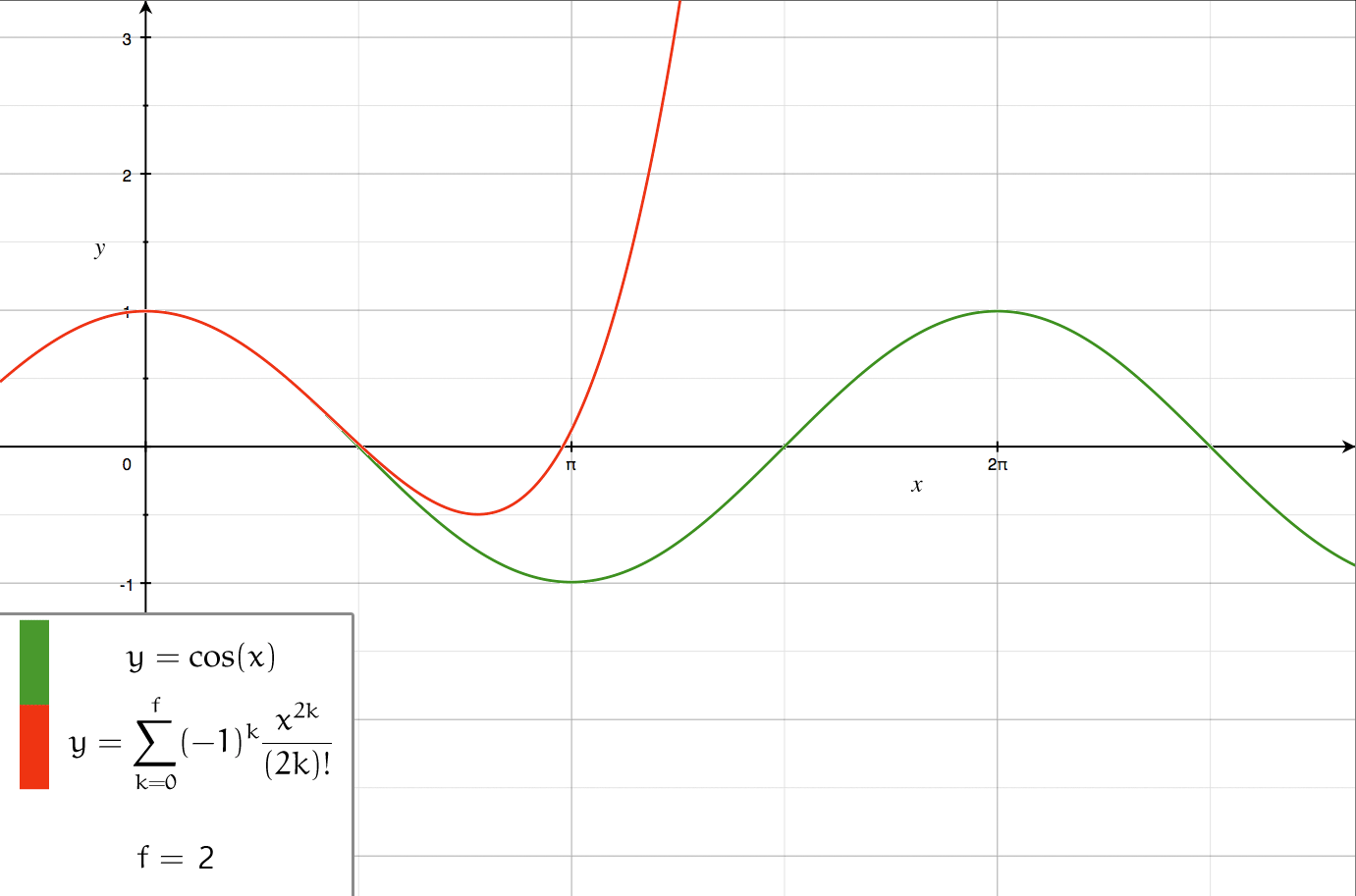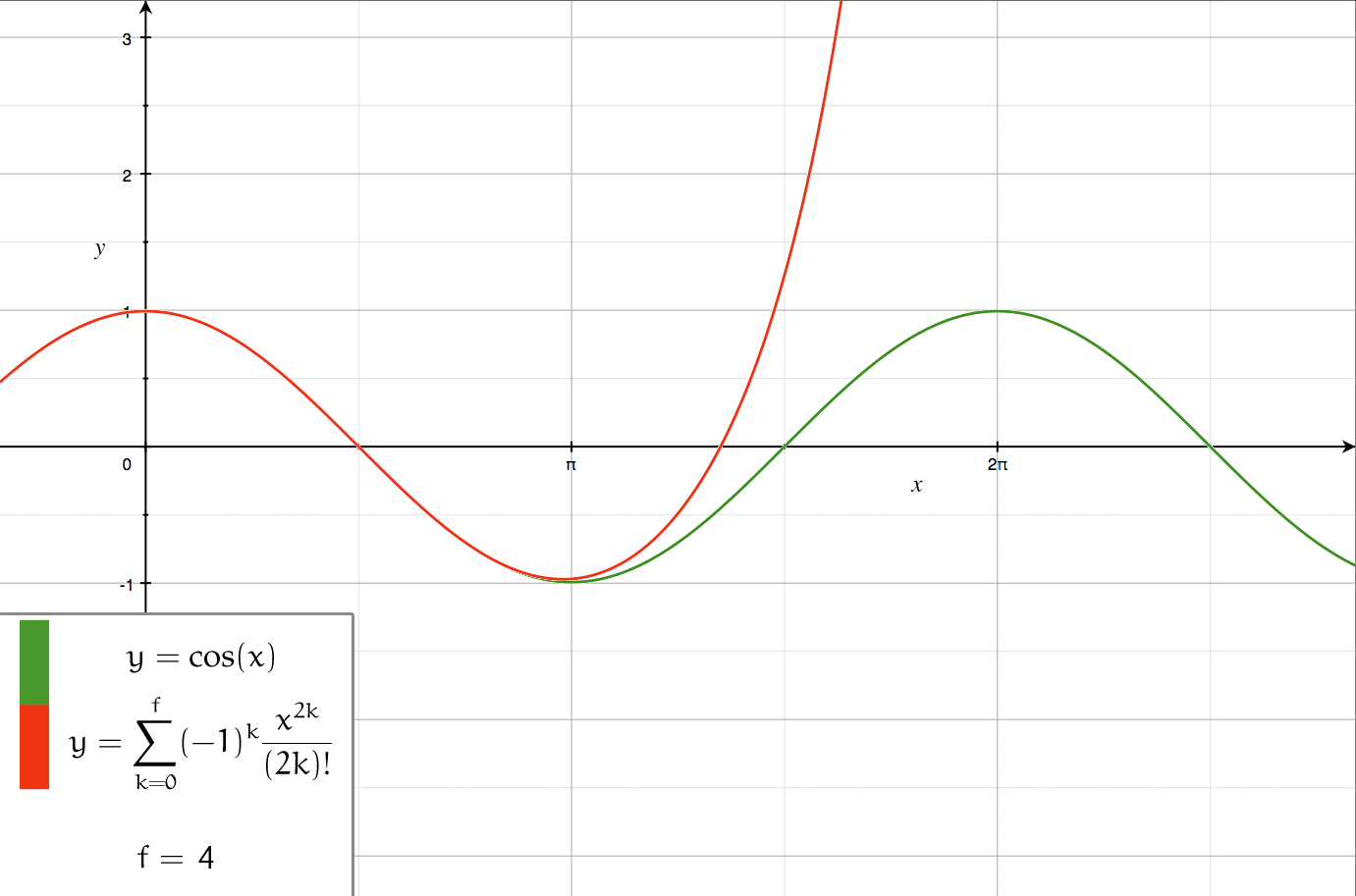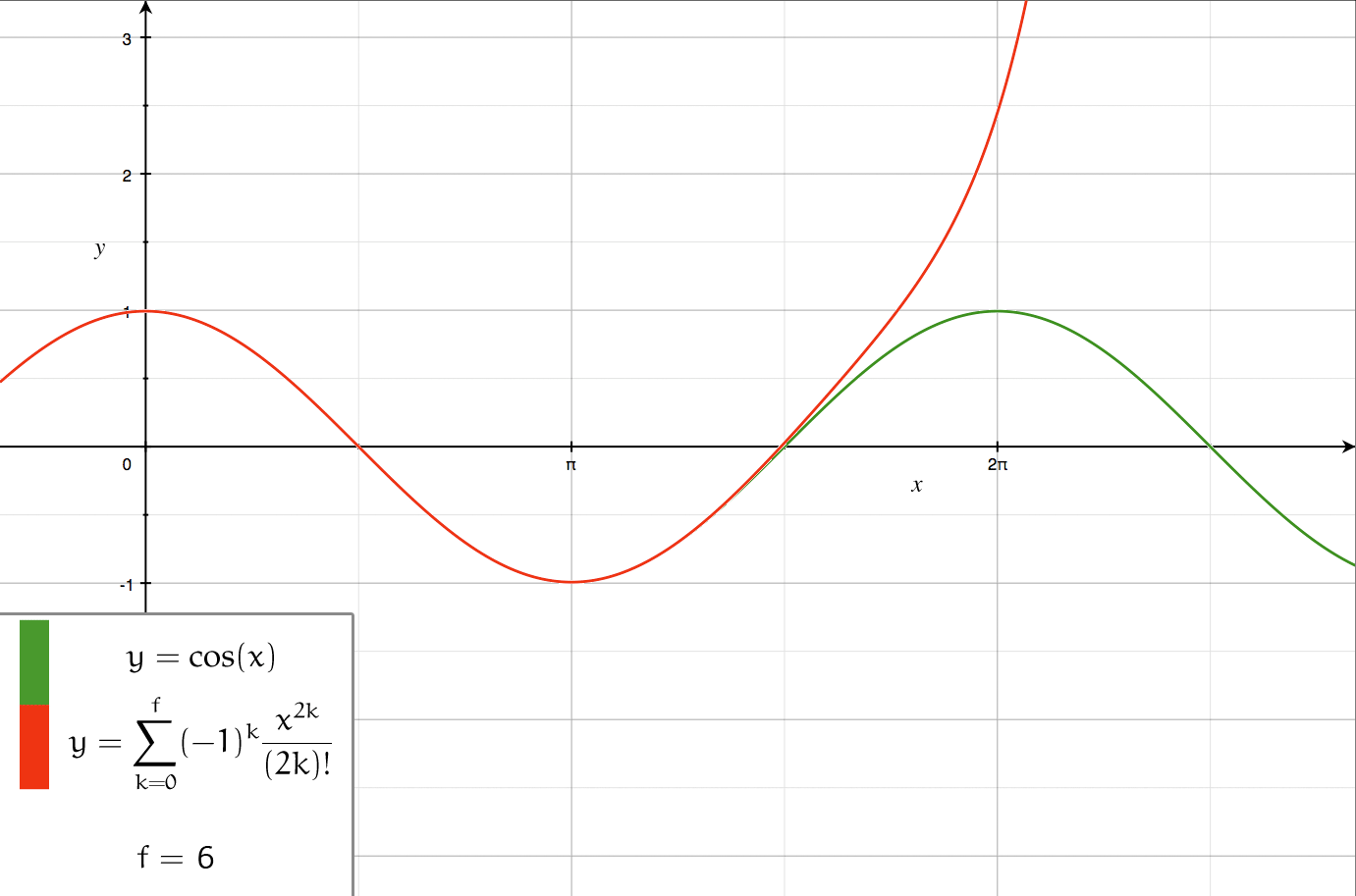
Axial multipole moments are a series expansion of the electric potential of a charge distribution localized close to the origin along one Cartesian axis, denoted here as the ''z''-axis. However, the axial multipole expansion can also be applied to any potential or field that varies inversely with the distance to the source, i.e., as \frac. For clarity, we first illustrate the expansion for a single point charge, then generalize to an arbitrary charge density \lambda(z) localized to the ''z''-axis. Axial multipole moments of a point charge The electric potential of a point charge ''q'' located on the ''z''-axis at z=a (Fig. 1) equals \Phi(\mathbf) = \frac \frac = \frac \frac. If the radius ''r'' of the observation point is greater than ''a'', we may factor out \frac and expand the square root in powers of (a/r)<1 using |
Series Expansion
In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called ''series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function f: U\to\mathbb is infinitely differentiable around ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coordinate System
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is significant, and they are sometimes identified by their position in an ordered tuple and sometimes by a letter, as in "the ''x''-coordinate". The coordinates are taken to be real numbers in elementary mathematics, but may be complex numbers or elements of a more abstract system such as a commutative ring. The use of a coordinate system allows problems in geometry to be translated into problems about numbers and ''vice versa''; this is the basis of analytic geometry. Common coordinate systems Number line The simplest example of a coordinate system is the identification of points on a line with real numbers using the ''number line''. In this system, an arbitrary point ''O'' (the ''origin'') is chosen on a given line. The coordinate of a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Laplace Expansion (potential)
In physics, the Laplace expansion of potentials that are directly proportional to the inverse of the distance ( 1/r ), such as Newton's gravitational potential or Coulomb's electrostatic potential, expresses them in terms of the spherical Legendre polynomials. In quantum mechanical calculations on atoms the expansion is used in the evaluation of integrals of the inter-electronic repulsion. The Laplace expansion is in fact the expansion of the inverse distance between two points. Let the points have position vectors \textbf and \textbf' , then the Laplace expansion is : \frac = \sum_^\infty \frac \sum_^ (-1)^m \frac Y^_\ell(\theta, \varphi) Y^m_\ell(\theta', \varphi'). Here \textbf has the spherical polar coordinates (r, \theta, \varphi) and \textbf' has (r', \theta', \varphi') with homogeneous polynomials of degree \ell . Further ''r''< is min(''r'', ''r''′) and ''r''> is max(''r'', ''r''′). The function Y^m_\ell is a normalized ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Harmonics
In physics and mathematics, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates, assumed to be (smooth) functions \mathbb^3 \to \mathbb. There are two kinds: the ''regular solid harmonics'' R^m_\ell(\mathbf), which are well-defined at the origin and the ''irregular solid harmonics'' I^m_(\mathbf), which are singular at the origin. Both sets of functions play an important role in potential theory, and are obtained by rescaling spherical harmonics appropriately: R^m_(\mathbf) \equiv \sqrt\; r^\ell Y^m_(\theta,\varphi) I^m_(\mathbf) \equiv \sqrt \; \frac Derivation, relation to spherical harmonics Introducing , , and for the spherical polar coordinates of the 3-vector , and assuming that \Phi is a (smooth) function \mathbb^3 \to \mathbb, we can write the Laplace equation in the following form \nabla^2\Phi(\mathbf) = \left(\frac \fracr - \frac\right)\Phi(\mathbf) = 0 , \qquad \mathbf \ne \mathbf, where is the square of the nondimensional ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cylindrical Multipole Moments
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R. Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential. For clarity, we illustrate the expansion for a single line charge, then generalize to an arbitrary distribution of line charges. Through this article, the primed coordinates such as (\rho^, \theta^) refer to the position of the line charge(s), whereas the unprimed coordinates such as (\rho, \theta) refer to the point at which the potential is being observed. We use cylindrical coordinates throughout, e.g., an arbitrary vector \mathbf has coordinates ( \rho, \theta, z) where \rho is the radius from the z axis, \theta is the azimuthal angle and z is the normal Cartesian coordinate. By assumption, the line charges are infinitely long and aligned with the z axis. Cylindr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spherical Multipole Moments
Spherical multipole moments are the coefficients in a series expansion of a potential that varies inversely with the distance R to a source, ''i.e.'', as 1/''R''. Examples of such potentials are the electric potential, the magnetic potential and the gravitational potential. For clarity, we illustrate the expansion for a point charge, then generalize to an arbitrary charge density \rho(\mathbf r'). Through this article, the primed coordinates such as \mathbf r' refer to the position of charge(s), whereas the unprimed coordinates such as \mathbf refer to the point at which the potential is being observed. We also use spherical coordinates throughout, e.g., the vector \mathbf r' has coordinates ( r', \theta', \phi') where r' is the radius, \theta' is the colatitude and \phi' is the azimuthal angle. Spherical multipole moments of a point charge The electric potential due to a point charge located at \mathbf is given by \Phi(\mathbf) = \frac \frac = \frac \frac. where R \ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multipole Expansion
A multipole expansion is a mathematical series representing a function that depends on angles—usually the two angles used in the spherical coordinate system (the polar and azimuthal angles) for three-dimensional Euclidean space, \R^3. Similarly to Taylor series, multipole expansions are useful because oftentimes only the first few terms are needed to provide a good approximation of the original function. The function being expanded may be real- or complex-valued and is defined either on \R^3, or less often on \R^n for some other Multipole expansions are used frequently in the study of electromagnetic and gravitational fields, where the fields at distant points are given in terms of sources in a small region. The multipole expansion with angles is often combined with an expansion in radius. Such a combination gives an expansion describing a function throughout three-dimensional space. The multipole expansion is expressed as a sum of terms with progressively finer angular featur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Potential Theory
In mathematics and mathematical physics, potential theory is the study of harmonic functions. The term "potential theory" was coined in 19th-century physics when it was realized that two fundamental forces of nature known at the time, namely gravity and the electrostatic force, could be modeled using functions called the gravitational potential and electrostatic potential, both of which satisfy Poisson's equation—or in the vacuum, Laplace's equation. There is considerable overlap between potential theory and the theory of Poisson's equation to the extent that it is impossible to draw a distinction between these two fields. The difference is more one of emphasis than subject matter and rests on the following distinction: potential theory focuses on the properties of the functions as opposed to the properties of the equation. For example, a result about the singularities of harmonic functions would be said to belong to potential theory whilst a result on how the solution depends ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respectively). Like charges repel each other and unlike charges attract each other. An object with an absence of net charge is referred to as neutral. Early knowledge of how charged substances interact is now called classical electrodynamics, and is still accurate for problems that do not require consideration of quantum effects. Electric charge is a conserved property; the net charge of an isolated system, the amount of positive charge minus the amount of negative charge, cannot change. Electric charge is carried by subatomic particles. In ordinary matter, negative charge is carried by electrons, and positive charge is carried by the protons in the nuclei of atoms. If there are more electrons than protons in a piece of matter, it will have ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure reflecting various orders of complexity. Mathematical definition The quadrupole moment tensor ''Q'' is a rank-two tensor—3×3 matrix. There are several definitions, but it is normally stated in the traceless form (i.e. Q_ + Q_ + Q_ = 0). The quadrupole moment tensor has thus nine components, but because of transposition symmetry and Trace (linear algebra), zero-trace property, in this form only five of these are independent. For a discrete system of \ell point charges or masses in the case of a Quadrupole#Gravitational quadrupole, gravitational quadrupole, each with charge q_\ell, or mass m_\ell, and position \vec_\ell = \left(r_, r_, r_\right) relative to the coordinate system origin, the components of the ''Q'' matrix are defined by: : ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Electric Potential
The electric potential (also called the ''electric field potential'', potential drop, the electrostatic potential) is defined as the amount of work energy needed to move a unit of electric charge from a reference point to the specific point in an electric field. More precisely, it is the energy per unit charge for a test charge that is so small that the disturbance of the field under consideration is negligible. Furthermore, the motion across the field is supposed to proceed with negligible acceleration, so as to avoid the test charge acquiring kinetic energy or producing radiation. By definition, the electric potential at the reference point is zero units. Typically, the reference point is earth or a point at infinity, although any point can be used. In classical electrostatics, the electrostatic field is a vector quantity expressed as the gradient of the electrostatic potential, which is a scalar quantity denoted by or occasionally , equal to the electric potential energy o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dipole
In physics, a dipole () is an electromagnetic phenomenon which occurs in two ways: *An electric dipole deals with the separation of the positive and negative electric charges found in any electromagnetic system. A simple example of this system is a pair of charges of equal magnitude but opposite sign separated by some typically small distance. (A permanent electric dipole is called an electret.) *A magnetic dipole is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet is an example of a magnet with a permanent magnetic dipole moment. Dipoles, whether electric or magnetic, can be characterized by their dipole moment, a vector quantity. For the simple electric dipole, the electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |