|
Argument Of A Function
In mathematics, an argument of a function is a value provided to obtain the function's result. It is also called an independent variable. For example, the binary function f(x,y) = x^2 + y^2 has two arguments, x and y, in an ordered pair (x, y). The hypergeometric function is an example of a four-argument function. The number of arguments that a function takes is called the ''arity'' of the function. A function that takes a single argument as input, such as f(x) = x^2, is called a unary function. A function of two or more variables is considered to have a domain consisting of ordered pairs or tuples of argument values. The argument of a circular function is an angle In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R .... The argument of a hyperbolic function is a hyperbolic ang ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle. More generally angles are also formed wherever two lines, rays or line segments come together, such as at the corners of triangles and other polygons. An angle can be considered as the region of the plane bounded by the sides. Angles can also be formed by the intersection of two planes or by two intersecting curves, in which case the rays lying tangent to each curve at the point of intersection define the angle. The term ''angle'' is also used for the size, magnitude (mathematics), magnitude or Physical quantity, quantity of these types of geometric figures and in this context an a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Astronomy
Astronomy is a natural science that studies celestial objects and the phenomena that occur in the cosmos. It uses mathematics, physics, and chemistry in order to explain their origin and their overall evolution. Objects of interest include planets, natural satellite, moons, stars, nebulae, galaxy, galaxies, meteoroids, asteroids, and comets. Relevant phenomena include supernova explosions, gamma ray bursts, quasars, blazars, pulsars, and cosmic microwave background radiation. More generally, astronomy studies everything that originates beyond atmosphere of Earth, Earth's atmosphere. Cosmology is a branch of astronomy that studies the universe as a whole. Astronomy is one of the oldest natural sciences. The early civilizations in recorded history made methodical observations of the night sky. These include the Egyptian astronomy, Egyptians, Babylonian astronomy, Babylonians, Greek astronomy, Greeks, Indian astronomy, Indians, Chinese astronomy, Chinese, Maya civilization, M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant (as opposed to the total derivative, in which all variables are allowed to vary). Partial derivatives are used in vector calculus and differential geometry. The partial derivative of a function f(x, y, \dots) with respect to the variable x is variously denoted by It can be thought of as the rate of change of the function in the x-direction. Sometimes, for the partial derivative of z with respect to x is denoted as \tfrac. Since a partial derivative generally has the same arguments as the original function, its functional dependence is sometimes explicitly signified by the notation, such as in: f'_x(x, y, \ldots), \frac (x, y, \ldots). The symbol used to denote partial derivatives is ∂. One of the first known uses of this symbol in mathematics is by Marquis de Condorcet from 1770, who used it for partial differ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subscript
A subscript or superscript is a character (such as a number or letter) that is set slightly below or above the normal line of type, respectively. It is usually smaller than the rest of the text. Subscripts appear at or below the baseline, while superscripts are above. Subscripts and superscripts are perhaps most often used in formulas, mathematical expressions, and specifications of chemical compounds and isotopes, but have many other uses as well. In professional typography, subscript and superscript characters are not simply ordinary characters reduced in size; to keep them visually consistent with the rest of the font, typeface designers make them slightly heavier (i.e. medium or bold typography) than a reduced-size character would be. The vertical distance that sub- or superscripted text is moved from the original baseline varies by typeface and by use. In typesetting, such types are traditionally called " superior" and "inferior" letters, figures, etc., or just "superi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base Of A Logarithm
In mathematics, the logarithm of a number is the exponent by which another fixed value, the base, must be raised to produce that number. For example, the logarithm of to base is , because is to the rd power: . More generally, if , then is the logarithm of to base , written , so . As a single-variable function, the logarithm to base is the inverse of exponentiation with base . The logarithm base is called the ''decimal'' or ''common'' logarithm and is commonly used in science and engineering. The ''natural'' logarithm has the number as its base; its use is widespread in mathematics and physics because of its very simple derivative. The ''binary'' logarithm uses base and is widely used in computer science, information theory, music theory, and photography. When the base is unambiguous from the context or irrelevant it is often omitted, and the logarithm is written . Logarithms were introduced by John Napier in 1614 as a means of simplifying calculations. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logarithmic Function
{{mathematical disambiguation ...
Logarithmic can refer to: * Logarithm, a transcendental function in mathematics * Logarithmic scale, the use of the logarithmic function to describe measurements * Logarithmic spiral, * Logarithmic growth * Logarithmic distribution, a discrete probability distribution * Natural logarithm The natural logarithm of a number is its logarithm to the base of a logarithm, base of the e (mathematical constant), mathematical constant , which is an Irrational number, irrational and Transcendental number, transcendental number approxima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system theory, system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
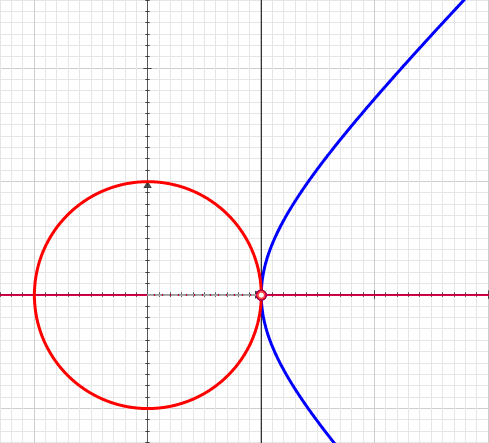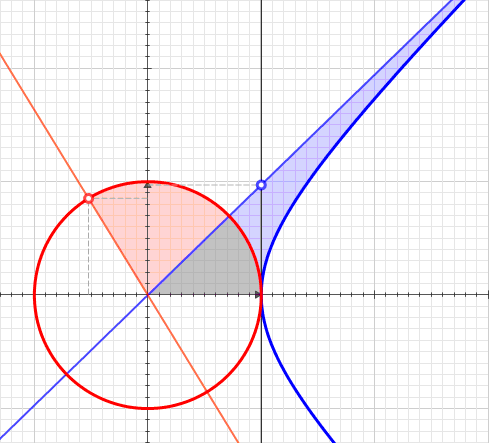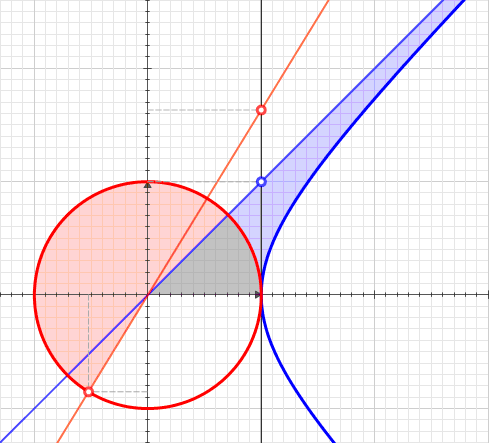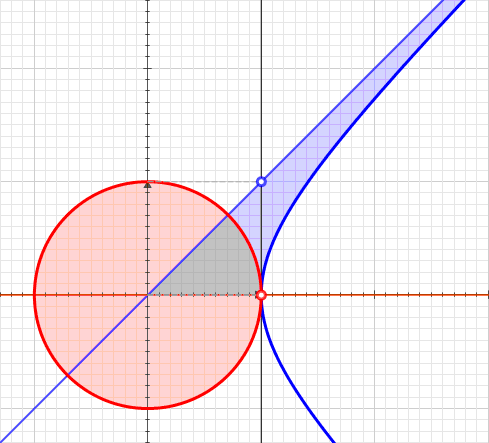
Hyperbolic Angle
In geometry, hyperbolic angle is a real number determined by the area of the corresponding hyperbolic sector of ''xy'' = 1 in Quadrant I of the Cartesian plane. The hyperbolic angle parametrizes the unit hyperbola, which has hyperbolic functions as coordinates. In mathematics, hyperbolic angle is an invariant measure as it is preserved under hyperbolic rotation. The hyperbola ''xy'' = 1 is rectangular with semi-major axis \sqrt 2, analogous to the circular angle equaling the area of a circular sector in a circle with radius \sqrt 2. Hyperbolic angle is used as the independent variable for the hyperbolic functions sinh, cosh, and tanh, because these functions may be premised on hyperbolic analogies to the corresponding circular (trigonometric) functions by regarding a hyperbolic angle as defining a hyperbolic triangle. The parameter thus becomes one of the most useful in the calculus of real variables. Definition Consider the rectangular hyperbola \textstyle\, and (by ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the unit hyperbola. Also, similarly to how the derivatives of and are and respectively, the derivatives of and are and respectively. Hyperbolic functions are used to express the angle of parallelism in hyperbolic geometry. They are used to express Lorentz boosts as hyperbolic rotations in special relativity. They also occur in the solutions of many linear differential equations (such as the equation defining a catenary), cubic equations, and Laplace's equation in Cartesian coordinates. Laplace's equations are important in many areas of physics, including electromagnetic theory, heat transfer, and fluid dynamics. The basic hyperbolic functions are: * hyperbolic sine "" (), * hyperbolic cosine "" (),''Collins Concise Dictio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Circular Function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent functions. Their multiplicative inverse, reciprocals are respectively the cosecant, the secant, and the cotangent functions, which are less used. Each of these six trigonometric functions has a corresponding Inverse trigonometric functions, inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Function (mathematics)
In mathematics, a function from a set (mathematics), set to a set assigns to each element of exactly one element of .; the words ''map'', ''mapping'', ''transformation'', ''correspondence'', and ''operator'' are sometimes used synonymously. The set is called the Domain of a function, domain of the function and the set is called the codomain of the function. Functions were originally the idealization of how a varying quantity depends on another quantity. For example, the position of a planet is a ''function'' of time. History of the function concept, Historically, the concept was elaborated with the infinitesimal calculus at the end of the 17th century, and, until the 19th century, the functions that were considered were differentiable function, differentiable (that is, they had a high degree of regularity). The concept of a function was formalized at the end of the 19th century in terms of set theory, and this greatly increased the possible applications of the concept. A f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |