|
Algorithmics
Algorithmics is the systematic study of the design and analysis of algorithms. It is fundamental and one of the oldest fields of computer science. It includes algorithm design, the art of building a procedure which can solve efficiently a specific problem or a class of problem, algorithmic complexity theory, the study of estimating the hardness of problems by studying the properties of the algorithm that solves them, or algorithm analysis, the science of studying the properties of a problem, such as quantifying resources in time and memory space needed by this algorithm to solve this problem. The term algorithmics is rarely used in the English-speaking world, where it is synonymous with ''algorithms and data structures''. The term gained wider popularity after the publication of the book ''Algorithmics: The Spirit of Computing'' by David Harel. See also * Divide-and-conquer algorithm * Heuristic A heuristic (; ), or heuristic technique, is any approach to problem solving ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (including the design and implementation of hardware and software). Computer science is generally considered an area of academic research and distinct from computer programming. Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and for preventing security vulnerabilities. Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of repositories ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm can be expressed within a finite amount of spac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm Design
In mathematics and computer science, an algorithm () is a finite sequence of rigorous instructions, typically used to solve a class of specific problems or to perform a computation. Algorithms are used as specifications for performing calculations and data processing. More advanced algorithms can perform automated deductions (referred to as automated reasoning) and use mathematical and logical tests to divert the code execution through various routes (referred to as automated decision-making). Using human characteristics as descriptors of machines in metaphorical ways was already practiced by Alan Turing with terms such as "memory", "search" and "stimulus". In contrast, a heuristic is an approach to problem solving that may not be fully specified or may not guarantee correct or optimal results, especially in problem domains where there is no well-defined correct or optimal result. As an effective method, an algorithm can be expressed within a finite amount of space and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
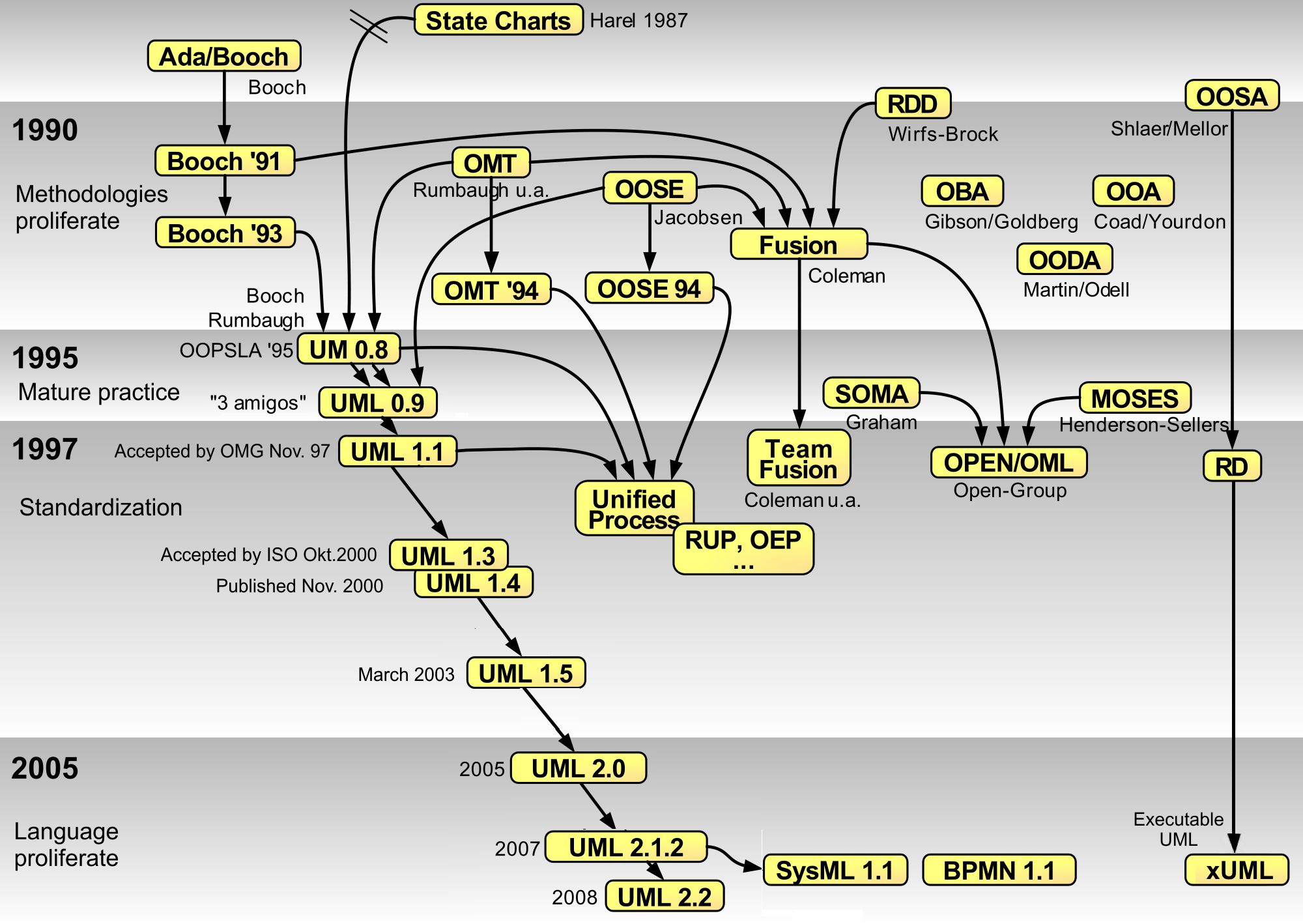
David Harel
David Harel ( he, דוד הראל; born 12 April 1950) is a computer scientist, currently serving as President of the Israel Academy of Sciences and Humanities. He has been on the faculty of the Weizmann Institute of Science in Israel since 1980, and holds the William Sussman Professorial Chair of Mathematics. Born in London, England, he was Dean of the Faculty of Mathematics and Computer Science at the institute for seven years. Biography Harel is best known for his work on dynamic logic, computability, database theory, software engineering and modelling biological systems. In the 1980s he invented the graphical language of Statecharts for specifying and programming reactive systems, which has been adopted as part of the UML standard. Since the late 1990s he has concentrated on a scenario-based approach to programming such systems, launched by his co-invention (with W. Damm) of Live Sequence Charts. He has published expository accounts of computer science, such as his awa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divide-and-conquer Algorithm
In computer science, divide and conquer is an algorithm design paradigm. A divide-and-conquer algorithm recursively breaks down a problem into two or more sub-problems of the same or related type, until these become simple enough to be solved directly. The solutions to the sub-problems are then combined to give a solution to the original problem. The divide-and-conquer technique is the basis of efficient algorithms for many problems, such as sorting (e.g., quicksort, merge sort), multiplying large numbers (e.g., the Karatsuba algorithm), finding the closest pair of points, syntactic analysis (e.g., top-down parsers), and computing the discrete Fourier transform ( FFT). Designing efficient divide-and-conquer algorithms can be difficult. As in mathematical induction, it is often necessary to generalize the problem to make it amenable to a recursive solution. The correctness of a divide-and-conquer algorithm is usually proved by mathematical induction, and its computational cos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithmic Complexity Theory
In algorithmic information theory (a subfield of computer science and mathematics), the Kolmogorov complexity of an object, such as a piece of text, is the length of a shortest computer program (in a predetermined programming language) that produces the object as output. It is a measure of the computational resources needed to specify the object, and is also known as algorithmic complexity, Solomonoff–Kolmogorov–Chaitin complexity, program-size complexity, descriptive complexity, or algorithmic entropy. It is named after Andrey Kolmogorov, who first published on the subject in 1963 and is a generalization of classical information theory. The notion of Kolmogorov complexity can be used to state and prove impossibility results akin to Cantor's diagonal argument, Gödel's incompleteness theorem, and Turing's halting problem. In particular, no program ''P'' computing a lower bound for each text's Kolmogorov complexity can return a value essentially larger than ''P'''s own l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithm Analysis
In computer science, the analysis of algorithms is the process of finding the computational complexity of algorithms—the amount of time, storage, or other resources needed to execute them. Usually, this involves determining a function that relates the size of an algorithm's input to the number of steps it takes (its time complexity) or the number of storage locations it uses (its space complexity). An algorithm is said to be efficient when this function's values are small, or grow slowly compared to a growth in the size of the input. Different inputs of the same size may cause the algorithm to have different behavior, so best, worst and average case descriptions might all be of practical interest. When not otherwise specified, the function describing the performance of an algorithm is usually an upper bound, determined from the worst case inputs to the algorithm. The term "analysis of algorithms" was coined by Donald Knuth. Algorithm analysis is an important part of a broader ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heuristic (computer Science)
In mathematical optimization and computer science, heuristic (from Greek εὑρίσκω "I find, discover") is a technique designed for solving a problem more quickly when classic methods are too slow for finding an approximate solution, or when classic methods fail to find any exact solution. This is achieved by trading optimality, completeness, accuracy, or precision for speed. In a way, it can be considered a shortcut. A heuristic function, also simply called a heuristic, is a function that ranks alternatives in search algorithms at each branching step based on available information to decide which branch to follow. For example, it may approximate the exact solution. Definition and motivation The objective of a heuristic is to produce a solution in a reasonable time frame that is good enough for solving the problem at hand. This solution may not be the best of all the solutions to this problem, or it may simply approximate the exact solution. But it is still valuabl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Akra–Bazzi Method
In computer science, the Akra–Bazzi method, or Akra–Bazzi theorem, is used to analyze the asymptotic behavior of the mathematical recurrences that appear in the analysis of divide and conquer algorithms where the sub-problems have substantially different sizes. It is a generalization of the master theorem for divide-and-conquer recurrences, which assumes that the sub-problems have equal size. It is named after mathematicians Mohamad Akra and Louay Bazzi. Formulation The Akra–Bazzi method applies to recurrence formulas of the form :T(x)=g(x) + \sum_^k a_i T(b_i x + h_i(x))\qquad \textx \geq x_0. The conditions for usage are: * sufficient base cases are provided * a_i and b_i are constants for all i * a_i > 0 for all i * 0 0, and can thus be computed using the Akra–Bazzi method to be \Theta(n \log n). See also * Master theorem (analysis of algorithms) * Asymptotic complexity References External links O Método de Akra-Bazzi na Resolução de Equações de R ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |