|
Algorithmic Mechanism Design
Algorithmic mechanism design (AMD) lies at the intersection of economic game theory, optimization, and computer science. The prototypical problem in mechanism design is to design a system for multiple self-interested participants, such that the participants' self-interested actions at equilibrium lead to good system performance. Typical objectives studied include revenue maximization and social welfare maximization. Algorithmic mechanism design differs from classical economic mechanism design in several respects. It typically employs the analytic tools of theoretical computer science, such as worst case analysis and approximation ratios, in contrast to classical mechanism design in economics which often makes distributional assumptions about the agents. It also considers computational constraints to be of central importance: mechanisms that cannot be efficiently implemented in polynomial time are not considered to be viable solutions to a mechanism design problem. This often, for exa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Game Theory
Game theory is the study of mathematical models of strategic interactions. It has applications in many fields of social science, and is used extensively in economics, logic, systems science and computer science. Initially, game theory addressed two-person zero-sum games, in which a participant's gains or losses are exactly balanced by the losses and gains of the other participant. In the 1950s, it was extended to the study of non zero-sum games, and was eventually applied to a wide range of Human behavior, behavioral relations. It is now an umbrella term for the science of rational Decision-making, decision making in humans, animals, and computers. Modern game theory began with the idea of mixed-strategy equilibria in two-person zero-sum games and its proof by John von Neumann. Von Neumann's original proof used the Brouwer fixed-point theorem on continuous mappings into compact convex sets, which became a standard method in game theory and mathematical economics. His paper was f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. Optimization problems Opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computer Science
Computer science is the study of computation, information, and automation. Computer science spans Theoretical computer science, theoretical disciplines (such as algorithms, theory of computation, and information theory) to Applied science, applied disciplines (including the design and implementation of Computer architecture, hardware and Software engineering, software). Algorithms and data structures are central to computer science. The theory of computation concerns abstract models of computation and general classes of computational problem, problems that can be solved using them. The fields of cryptography and computer security involve studying the means for secure communication and preventing security vulnerabilities. Computer graphics (computer science), Computer graphics and computational geometry address the generation of images. Programming language theory considers different ways to describe computational processes, and database theory concerns the management of re ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
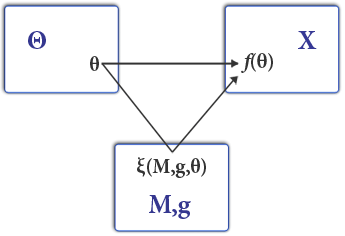
Mechanism Design
Mechanism design (sometimes implementation theory or institution design) is a branch of economics and game theory. It studies how to construct rules—called Game form, mechanisms or institutions—that produce good outcomes according to Social welfare function, some predefined metric, even when the designer does not know the players' true preferences or what information they have. Mechanism design thus focuses on the study of solution concepts for a class of private-information games. Mechanism design has broad applications, including traditional domains of economics such as market design, but also political science (through voting theory). It is a foundational component in the operation of the internet, being used in networked systems (such as inter-domain routing), e-commerce, and Sponsored search auction, advertisement auctions by Facebook and Google. Because it starts with the end of the game (a particular result), then works backwards to find a game that implements it, it ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Theoretical Computer Science
Theoretical computer science is a subfield of computer science and mathematics that focuses on the Abstraction, abstract and mathematical foundations of computation. It is difficult to circumscribe the theoretical areas precisely. The Association for Computing Machinery, ACM's Special Interest Group on Algorithms and Computation Theory (SIGACT) provides the following description: History While logical inference and mathematical proof had existed previously, in 1931 Kurt Gödel proved with his incompleteness theorem that there are fundamental limitations on what statements could be proved or disproved. Information theory was added to the field with A Mathematical Theory of Communication, a 1948 mathematical theory of communication by Claude Shannon. In the same decade, Donald Hebb introduced a mathematical model of Hebbian learning, learning in the brain. With mounting biological data supporting this hypothesis with some modification, the fields of neural networks and para ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Worst Case Analysis
Worst case analysis was, from 1978 until 1986, a doctrine under which mandated that an environmental impact statement include such an analysis: It led to a 1989 SCOTUS decision, written by John Paul Stevens and reported in '' Robertson v. Methow Valley Citizens Council'',Ecology Law Quarterly Volume 18 Issue 1 Article 5 January 1991: Marion D. Miller"The National Environmental Policy Act and Judicial Review after Robertson v. Methow Valley Citizens Council and Marsh v. Oregon Natural Resources Council"/ref> after a decision by GOODWIN and FERGUSON, STEPHENS to reverse the Federal District Court of Oregon ruling that the Regional Forester did not violate any laws when he issued a special use permit for a ski resort development in a roadless area in Okanogan National Forest in Washington state. The Rehnquist Court The Rehnquist Court was the period in the history of the Supreme Court of the United States during which William Rehnquist served as Chief Justice. Rehnquist succee ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Approximation Ratio
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned solution to the optimal one. Approximation algorithms naturally arise in the field of theoretical computer science as a consequence of the widely believed P ≠ NP conjecture. Under this conjecture, a wide class of optimization problems cannot be solved exactly in polynomial time. The field of approximation algorithms, therefore, tries to understand how closely it is possible to approximate optimal solutions to such problems in polynomial time. In an overwhelming majority of the cases, the guarantee of such algorithms is a multiplicative one expressed as an approximation ratio or approximation factor i.e., the optimal solution is always guaranteed to be within a (predetermined) multiplicative factor of the returned solution. However, there a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vickrey–Clarke–Groves Auction
A Vickrey–Clarke–Groves (VCG) auction is a type of sealed-bid auction of multiple items. Bidders submit bids that report their valuations for the items, without knowing the bids of the other bidders. The auction system assigns the items in a socially optimal manner: it charges each individual the harm they cause to other bidders. It gives bidders an incentive to bid their true valuations, by ensuring that the optimal strategy for each bidder is to bid their true valuations of the items; it can be undermined by bidder collusion and in particular in some circumstances by a single bidder making multiple bids under different names. It is a generalization of a Vickrey auction for multiple items. The auction is named after William Vickrey, Edward H. Clarke, and Theodore Groves for their papers that successively generalized the idea. The VCG auction is a specific use of the more general VCG mechanism. While the VCG auction tries to make a socially optimal allocation of items, V ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Noam Nisan
Noam Nisan (; born June 20, 1961) is an Israeli computer scientist and professor of computer science at the Hebrew University of Jerusalem. He is known for his research in computational complexity theory and algorithmic game theory. Biography Nisan did his undergraduate studies at the Hebrew University, graduating in 1984. He went to the University of California, Berkeley, for graduate school, and received a Ph.D. in 1988 under the supervision of Richard Karp. After postdoctoral studies at the Massachusetts Institute of Technology he joined the Hebrew University faculty in 1990.Curriculum vitae retrieved 2012-03-01. Selected publications Nisan is the author of[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Algorithmic Game Theory
Algorithmic game theory (AGT) is an interdisciplinary field at the intersection of game theory and computer science, focused on understanding and designing algorithms for environments where multiple strategic agents interact. This research area combines computational thinking with economic principles to address challenges that emerge when algorithmic inputs come from self-interested participants. In traditional algorithm design, inputs are assumed to be fixed and reliable. However, in many real-world applications—such as online auctions, internet routing, digital advertising, and resource allocation systems—inputs are provided by multiple independent agents who may strategically misreport information to manipulate outcomes in their favor. AGT provides frameworks to analyze and design systems that remain effective despite such strategic behavior. The field can be approached from two complementary perspectives: * ''Analysis'': Evaluating existing algorithms and systems throu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Computational Social Choice
A computation is any type of arithmetic or non-arithmetic calculation that is well-defined. Common examples of computation are mathematical equation solving and the execution of computer algorithms. Mechanical or electronic devices (or, historically, people) that perform computations are known as ''computers''. Computer science is an academic field that involves the study of computation. Introduction The notion that mathematical statements should be 'well-defined' had been argued by mathematicians since at least the 1600s, but agreement on a suitable definition proved elusive. A candidate definition was proposed independently by several mathematicians in the 1930s. The best-known variant was formalised by the mathematician Alan Turing, who defined a well-defined statement or calculation as any statement that could be expressed in terms of the initialisation parameters of a Turing machine. Other (mathematically equivalent) definitions include Alonzo Church's '' lambda-definabil ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metagame
A metagame, broadly defined as "a game beyond the game", typically refers to either of two concepts: a game which revolves around a core game; or the strategies and approaches to playing a game. A metagame can serve a broad range of purposes, and may be tied to the way a game relates to various aspects of life. In competitive games, the metagame can refer to the most popular strategy, often called a game's meta, or preparation for a match in general. In tabletop role-playing game, tabletop role-playing games, metagaming has been used to describe players discussing the game, sometimes simply rules discussions and other times causing the characters they control to act in ways they normally would not within the story. Etymology The word metagame is composed of the Greek language, Greek-derived prefix ''Meta (prefix), meta''– (from μετά, meta, meaning "after") and the noun ''game''. ''Metagame'' was used in the context of playing zero-sum games in a publication by the Menta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |