|
Algebraic Riccati Equation
An algebraic Riccati equation is a type of nonlinear equation that arises in the context of infinite-horizon optimal control problems in continuous time or discrete time. A typical algebraic Riccati equation is similar to one of the following: the continuous time algebraic Riccati equation (CARE): A^\top P + P A - P B R^ B^\top P + Q = 0 or the discrete time algebraic Riccati equation (DARE): P = A^\top P A -(A^\top P B)(R + B^\top P B)^(B^\top P A) + Q. is the unknown by symmetric matrix and are known real coefficient matrices, with and symmetric. Though generally this equation can have many solutions, it is usually specified that we want to obtain the unique stabilizing solution, if such a solution exists. Origin of the name The name Riccati is given to these equations because of their relation to the Riccati differential equation. Indeed, the CARE is verified by the time invariant solutions of the associated matrix valued Riccati differential equation. As ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Nonlinear System
In mathematics and science, a nonlinear system (or a non-linear system) is a system in which the change of the output is not proportional to the change of the input. Nonlinear problems are of interest to engineers, biologists, physicists, mathematicians, and many other scientists since most systems are inherently nonlinear in nature. Nonlinear dynamical systems, describing changes in variables over time, may appear chaotic, unpredictable, or counterintuitive, contrasting with much simpler linear systems. Typically, the behavior of a nonlinear system is described in mathematics by a nonlinear system of equations, which is a set of simultaneous equations in which the unknowns (or the unknown functions in the case of differential equations) appear as variables of a polynomial of degree higher than one or in the argument of a function which is not a polynomial of degree one. In other words, in a nonlinear system of equations, the equation(s) to be solved cannot be written as a lin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
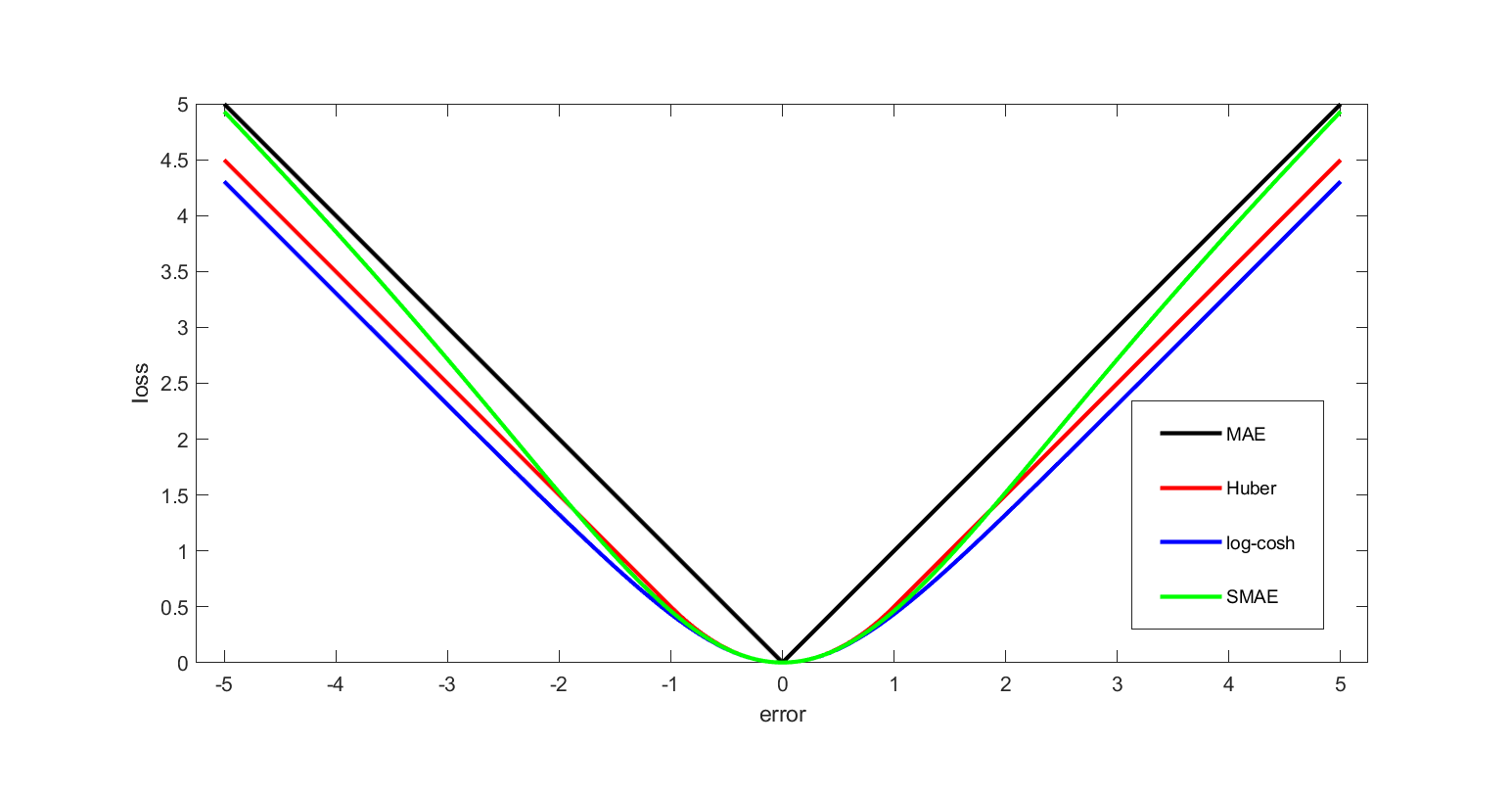
Loss Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Pierre-Simon Laplace, Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Matrices (mathematics)
Matrix (: matrices or matrixes) or MATRIX may refer to: Science and mathematics * Matrix (mathematics), a rectangular array of numbers, symbols or expressions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Technology * Matrix (mass spectrometry), a compound that promotes the formation of ions * Matrix (numismatics), a tool used in coin manufacturing * Matrix (printing), a mould for casting letters * Matrix (protocol), an open standard for real-time communication * Matrix (record production), or master, a disc used in the production of phonograph records ** Matrix number, of a gramophone record * D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Oxford University Press
Oxford University Press (OUP) is the publishing house of the University of Oxford. It is the largest university press in the world. Its first book was printed in Oxford in 1478, with the Press officially granted the legal right to print books by decree in 1586. It is the second-oldest university press after Cambridge University Press, which was founded in 1534. It is a department of the University of Oxford. It is governed by a group of 15 academics, the Delegates of the Press, appointed by the Vice Chancellor, vice-chancellor of the University of Oxford. The Delegates of the Press are led by the Secretary to the Delegates, who serves as OUP's chief executive and as its major representative on other university bodies. Oxford University Press has had a similar governance structure since the 17th century. The press is located on Walton Street, Oxford, Walton Street, Oxford, opposite Somerville College, Oxford, Somerville College, in the inner suburb of Jericho, Oxford, Jericho. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Sylvester Equation
In mathematics, in the field of control theory, a Sylvester equation is a matrix equation of the form: :A X + X B = C. It is named after English mathematician James Joseph Sylvester. Then given matrices ''A'', ''B'', and ''C'', the problem is to find the possible matrices ''X'' that obey this equation. All matrices are assumed to have coefficients in the complex numbers. For the equation to make sense, the matrices must have appropriate sizes, for example they could all be square matrices of the same size. But more generally, ''A'' and ''B'' must be square matrices of sizes ''n'' and ''m'' respectively, and then ''X'' and ''C'' both have ''n'' rows and ''m'' columns. A Sylvester equation has a unique solution for ''X'' exactly when there are no common eigenvalues of ''A'' and −''B''. More generally, the equation ''AX'' + ''XB'' = ''C'' has been considered as an equation of bounded operators on a (possibly infinite-dimensional) Banach space. In this case, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Schur Decomposition
In the mathematical discipline of linear algebra, the Schur decomposition or Schur triangulation, named after Issai Schur, is a matrix decomposition. It allows one to write an arbitrary complex square matrix as unitarily similar to an upper triangular matrix whose diagonal elements are the eigenvalues of the original matrix. Statement The complex Schur decomposition reads as follows: if is an square matrix with complex entries, then ''A'' can be expressed as (Section 2.3 and further at p. 79(Section 7.7 at p. 313 A = Q U Q^ for some unitary matrix ''Q'' (so that the inverse ''Q''−1 is also the conjugate transpose ''Q''* of ''Q''), and some upper triangular matrix ''U''. This is called a Schur form of ''A''. Since ''U'' is similar to ''A'', it has the same spectrum, and since it is triangular, its eigenvalues are the diagonal entries of ''U''. The Schur decomposition implies that there exists a nested sequence of ''A''-invariant subspaces , and that there exists an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Lyapunov Equation
The Lyapunov equation, named after the Russian mathematician Aleksandr Lyapunov, is a matrix equation used in the stability analysis of linear dynamical systems. In particular, the discrete-time Lyapunov equation (also known as Stein equation) for X is :A X A^ - X + Q = 0 where Q is a Hermitian matrix and A^H is the conjugate transpose of A, while the continuous-time Lyapunov equation is :AX + XA^H + Q = 0. Application to stability In the following theorems A, P, Q \in \mathbb^, and P and Q are symmetric. The notation P>0 means that the matrix P is positive definite. Theorem (continuous time version). Given any Q>0, there exists a unique P>0 satisfying A^T P + P A + Q = 0 if and only if the linear system \dot=A x is globally asymptotically stable. The quadratic function V(x)=x^T P x is a Lyapunov function that can be used to verify stability. Theorem (discrete time version). Given any Q>0, there exists a unique P>0 satisfying A^T P A -P + Q = 0 if and only if the linear ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symplectic Matrix
In mathematics, a symplectic matrix is a 2n\times 2n matrix M with real entries that satisfies the condition where M^\text denotes the transpose of M and \Omega is a fixed 2n\times 2n nonsingular, skew-symmetric matrix. This definition can be extended to 2n\times 2n matrices with entries in other fields, such as the complex numbers, finite fields, ''p''-adic numbers, and function fields. Typically \Omega is chosen to be the block matrix \Omega = \begin 0 & I_n \\ -I_n & 0 \\ \end, where I_n is the n\times n identity matrix. The matrix \Omega has determinant +1 and its inverse is \Omega^ = \Omega^\text = -\Omega. Properties Generators for symplectic matrices Every symplectic matrix has determinant +1, and the 2n\times 2n symplectic matrices with real entries form a subgroup of the general linear group \mathrm(2n;\mathbb) under matrix multiplication since being symplectic is a property stable under matrix multiplication. Topologically, this symplectic group is a conn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hamiltonian Matrix
In mathematics, a Hamiltonian matrix is a -by- matrix such that is symmetric, where is the skew-symmetric matrix :J = \begin 0_n & I_n \\ -I_n & 0_n \\ \end and is the -by- identity matrix. In other words, is Hamiltonian if and only if where denotes the transpose.. (Not to be confused with Hamiltonian (quantum mechanics)) Properties Suppose that the -by- matrix is written as the block matrix : A = \begin a & b \\ c & d \end where , , , and are -by- matrices. Then the condition that be Hamiltonian is equivalent to requiring that the matrices and are symmetric, and that .. Another equivalent condition is that is of the form with symmetric. It follows easily from the definition that the transpose of a Hamiltonian matrix is Hamiltonian. Furthermore, the sum (and any linear combination) of two Hamiltonian matrices is again Hamiltonian, as is their commutator. It follows that the space of all Hamiltonian matrices is a Lie algebra, denoted . The dimension of is . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
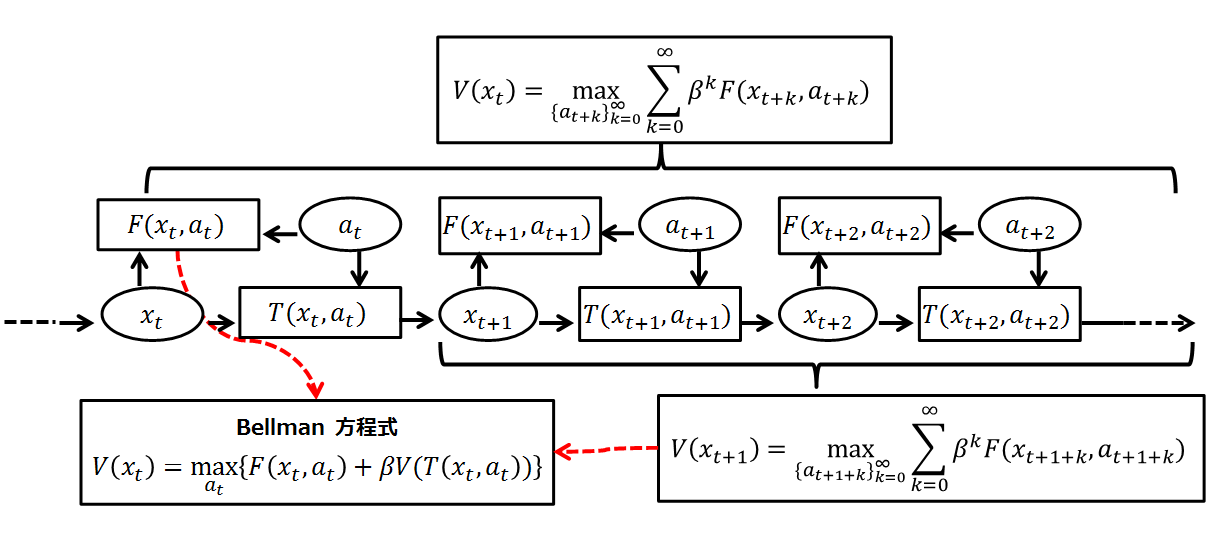
Bellman Equation
A Bellman equation, named after Richard E. Bellman, is a necessary condition for optimality associated with the mathematical Optimization (mathematics), optimization method known as dynamic programming. It writes the "value" of a decision problem at a certain point in time in terms of the payoff from some initial choices and the "value" of the remaining decision problem that results from those initial choices. This breaks a dynamic optimization problem into a sequence of simpler subproblems, as Bellman's “principle of optimality" prescribes. The equation applies to algebraic structures with a total ordering; for algebraic structures with a partial ordering, the generic Bellman's equation can be used. The Bellman equation was first applied to engineering control theory and to other topics in applied mathematics, and subsequently became an important tool in economic theory; though the basic concepts of dynamic programming are prefigured in John von Neumann and Oskar Morgenstern's ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Positive Definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to b ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Optimal Control
Optimal control theory is a branch of control theory that deals with finding a control for a dynamical system over a period of time such that an objective function is optimized. It has numerous applications in science, engineering and operations research. For example, the dynamical system might be a spacecraft with controls corresponding to rocket thrusters, and the objective might be to reach the Moon with minimum fuel expenditure. Or the dynamical system could be a nation's economy, with the objective to minimize unemployment; the controls in this case could be fiscal and monetary policy. A dynamical system may also be introduced to embed operations research problems within the framework of optimal control theory. Optimal control is an extension of the calculus of variations, and is a mathematical optimization method for deriving control policies. The method is largely due to the work of Lev Pontryagin and Richard Bellman in the 1950s, after contributions to calculus of v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |