|
Algebraic Petri Net
An algebraic Petri net (APN) is an evolution of the well known Petri net in which elements of user defined data types (called algebraic abstract data types (AADT)) replace black tokens. This formalism can be compared to coloured Petri nets (CPN) in many aspects. However, in the APN case, the semantics of the data types is given by an axiomatization enabling proofs and computations on it. Algebraic Petri nets were invented by Jacques Vautherin in 1985 in his PhD thesis and later improved by Wolfang Reisig. The formalism has two aspects : * The control part which is handled by a Petri net. * The data part which is handled by one or many AADTs. AADT can be themselves split in two parts: * The ''signature'' (Sort and Ops in the example below) which gives the valid constants and operations of the term algebra. * The ''axiomatization'' (Axioms in the example below) which gives the semantics of the operations described in the signature part. The following picture describes an algebraic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
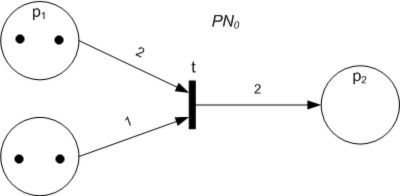
Petri Net
A Petri net, also known as a place/transition (PT) net, is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that has two types of elements, places and transitions. Place elements are depicted as white circles and transition elements are depicted as rectangles. A place can contain any number of tokens, depicted as black circles. A transition is enabled if all places connected to it as inputs contain at least one token. Some sources state that Petri nets were invented in August 1939 by Carl Adam Petri—at the age of 13—for the purpose of describing chemical processes. Like industry standards such as UML activity diagrams, Business Process Model and Notation, and event-driven process chains, Petri nets offer a graphical notation for stepwise processes that include choice, iteration, and concurrent execution. Unlike these standards, Petri nets hav ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coloured Petri Net
Coloured Petri nets are a backward compatible extension of the mathematical concept of Petri net A Petri net, also known as a place/transition (PT) net, is one of several mathematical modeling languages for the description of distributed systems. It is a class of discrete event dynamic system. A Petri net is a directed bipartite graph that ...s. Coloured Petri nets preserve useful properties of Petri nets and at the same time extend the initial formalism to allow the distinction between tokens. Coloured Petri nets allow tokens to have a data value attached to them. This attached data value is called the token color. Although the color can be of arbitrarily complex type, places in coloured Petri nets usually contain tokens of one type. This type is called the color set of the place. Definition 1. A ''net'' is a tuple ''N'' = (''P'', ''T'', ''A'', Σ, ''C'', ''N'', ''E'', ''G'', ''I'' ) where: * ''P'' is a set of ''places''. * ''T'' is a set of ''transitions''. * ''A'' is a set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axiomatization
In mathematics and logic, an axiomatic system is any Set (mathematics), set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A Theory (mathematical logic), theory is a consistent, relatively-self-contained body of knowledge which usually contains an axiomatic system and all its derived theorems. An axiomatic system that is completely described is a special kind of formal system. A formal theory is an axiomatic system (usually formulated within model theory) that describes a set of sentences that is closed under logical implication. A formal proof is a complete rendition of a mathematical proof within a formal system. Properties An axiomatic system is said to be ''Consistency, consistent'' if it lacks contradiction. That is, it is impossible to derive both a statement and its negation from the system's axioms. Consistency is a key requirement for most axiomatic systems, as the presence of contradiction would allow any statement to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Coloured Petri Nets
Coloured Petri nets are a backward compatible extension of the mathematical concept of Petri nets. Coloured Petri nets preserve useful properties of Petri nets and at the same time extend the initial formalism to allow the distinction between tokens. Coloured Petri nets allow tokens to have a data value attached to them. This attached data value is called the token color. Although the color can be of arbitrarily complex type, places in coloured Petri nets usually contain tokens of one type. This type is called the color set of the place. Definition 1. A ''net'' is a tuple ''N'' = (''P'', ''T'', ''A'', Σ, ''C'', ''N'', ''E'', ''G'', ''I'' ) where: * ''P'' is a set of ''places''. * ''T'' is a set of ''transitions''. * ''A'' is a set of ''arcs'' In coloured Petri nets, sets of places, transitions and arcs are pairwise disjoint ''P'' ∩ ''T'' = ''P'' ∩ ''A'' = ''T'' ∩ ''A'' = ∅ * Σ is a set of color sets. This set contains all possible colors, operations and functions used ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Term Algebra
In universal algebra and mathematical logic, a term algebra is a freely generated algebraic structure over a given signature. For example, in a signature consisting of a single binary operation, the term algebra over a set ''X'' of variables is exactly the free magma generated by ''X''. Other synonyms for the notion include absolutely free algebra and anarchic algebra. From a category theory perspective, a term algebra is the initial object for the category of all ''X''-generated algebras of the same signature, and this object, unique up to isomorphism, is called an initial algebra; it generates by homomorphic projection all algebras in the category. A similar notion is that of a Herbrand universe in logic, usually used under this name in logic programming, which is (absolutely freely) defined starting from the set of constants and function symbols in a set of clauses. That is, the Herbrand universe consists of all ground terms: terms that have no variables in them. An atomic for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dining Philosophers Problem
In computer science, the dining philosophers problem is an example problem often used in concurrent algorithm design to illustrate synchronization issues and techniques for resolving them. It was originally formulated in 1965 by Edsger Dijkstra as a student exam exercise, presented in terms of computers competing for access to tape drive peripherals. Soon after, Tony Hoare gave the problem its present form. Problem statement Five philosophers dine together at the same table. Each philosopher has their own place at the table. There is a fork between each plate. The dish served is a kind of spaghetti which has to be eaten with two forks. Each philosopher can only alternately think and eat. Moreover, a philosopher can only eat their spaghetti when they have both a left and right fork. Thus two forks will only be available when their two nearest neighbors are thinking, not eating. After an individual philosopher finishes eating, they will put down both forks. The problem is how to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multiset
In mathematics, a multiset (or bag, or mset) is a modification of the concept of a set that, unlike a set, allows for multiple instances for each of its elements. The number of instances given for each element is called the multiplicity of that element in the multiset. As a consequence, an infinite number of multisets exist which contain only elements and , but vary in the multiplicities of their elements: * The set contains only elements and , each having multiplicity 1 when is seen as a multiset. * In the multiset , the element has multiplicity 2, and has multiplicity 1. * In the multiset , and both have multiplicity 3. These objects are all different when viewed as multisets, although they are the same set, since they all consist of the same elements. As with sets, and in contrast to tuples, order does not matter in discriminating multisets, so and denote the same multiset. To distinguish between sets and multisets, a notation that incorporates square brackets is s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a well-formed formula, formula with other terms. Such methods may be achieved by rewriting systems (also known as rewrite systems, rewrite engines, or reduction systems). In their most basic form, they consist of a set of objects, plus relations on how to transform those objects. Rewriting can be non-deterministic algorithm, non-deterministic. One rule to rewrite a term could be applied in many different ways to that term, or more than one rule could be applicable. Rewriting systems then do not provide an algorithm for changing one term to another, but a set of possible rule applications. When combined with an appropriate algorithm, however, rewrite systems can be viewed as computer programs, and several automated theorem proving, theorem provers and declarative programming languages are based on term rewriting. Example cases Logic In logic, the procedure for obtaini ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
CO-OPN
The CO-OPN (Concurrent Object-Oriented Petri Nets) specification language is based on both algebraic specifications and algebraic Petri nets formalisms. The former formalism represent the data structures aspects, while the latter stands for the behavioral and concurrent aspects of systems. In order to deal with large specifications some structuring capabilities have been introduced. The object-oriented paradigm has been adopted, which means that a CO-OPN specification is a collection of objects which interact concurrently. Cooperation between the objects is achieved by means of a synchronization mechanism, i.e., each object event may request to be synchronized with some methods (parameterized events) of one or a group of partners by means of a synchronization expression. A CO-OPN specification consists of a collection of two different modules: the abstract data type modules and the object modules. The abstract data type modules concern the data structure component of the specifica ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specification Languages
A specification often refers to a set of documented requirements to be satisfied by a material, design, product, or service. A specification is often a type of technical standard. There are different types of technical or engineering specifications (specs), and the term is used differently in different technical contexts. They often refer to particular documents, and/or particular information within them. The word ''specification'' is broadly defined as "to state explicitly or in detail" or "to be specific". A requirement specification is a documented requirement, or set of documented requirements, to be satisfied by a given material, design, product, service, etc. It is a common early part of engineering design and product development processes in many fields. A functional specification is a kind of requirement specification, and may show functional block diagrams. A design or product specification describes the features of the ''solutions'' for the Requirement Specification, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |