|
Actuarial Notation
Actuarial notation is a shorthand method to allow actuaries to record mathematical formulas that deal with interest rates and life tables. Traditional notation uses a halo system, where symbols are placed as superscript or subscript before or after the main letter. Example notation using the halo system can be seen to the right. Various proposals have been made to adopt a linear system, where all the notation would be on a single line without the use of superscripts or subscripts. Such a method would be useful for computing where representation of the halo system can be extremely difficult. However, a standard linear system has yet to emerge. Example notation Interest rates \,i is the annual effective interest rate, which is the "true" rate of interest over ''a year''. Thus if the annual interest rate is 12% then \,i = 0.12. \,i^ (pronounced "i ''upper'' m") is the nominal interest rate convertible m times a year, and is numerically equal to m times the effective rate of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Annual Effective Discount Rate
The annual effective discount rate expresses the amount of interest paid or earned as a ''percentage'' of the balance at the ''end'' of the annual period. It is related to but slightly smaller than the effective rate of interest, which expresses the amount of interest as a ''percentage'' of the balance at the ''start'' of the period. The discount rate is commonly used for U.S. Treasury bills and similar financial instruments. For example, consider a government bond that sells for $95 ('balance' in the bond at the start of period) and pays $100 ('balance' in the bond at the end of period) in a year's time. The discount rate is : \frac = 5.00\% The effective interest rate is calculated using 95 as the base : \frac = 5.26\% which says that 95\% of $105.26 is $100. For every effective interest rate i, there is a corresponding effective discount rate d that can produce the same future value as i if a given amount of principal is invested for the same amount of time at each of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Life Insurance
Life insurance (or life assurance, especially in the Commonwealth of Nations) is a contract A contract is an agreement that specifies certain legally enforceable rights and obligations pertaining to two or more parties. A contract typically involves consent to transfer of goods, services, money, or promise to transfer any of thos ... between an insurance policy holder and an insurance , insurer or assurer, where the insurer promises to pay a designated beneficiary a sum of money upon the death of an insured person. Depending on the contract, other events such as terminal illness or critical illness can also trigger payment. The policyholder typically pays a premium, either regularly or as one lump sum. The benefits may include other expenses, such as funeral expenses. Life policies are legal contracts and the terms of each contract describe the limitations of the insured events. Often, specific exclusions written into the contract limit the liability of the insurer; c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Actuarial Present Value
The actuarial present value (APV) is the expected value of the present value of a contingent cash flow stream (i.e. a series of payments which may or may not be made). Actuarial present values are typically calculated for the benefit-payment or series of payments associated with life insurance and life annuities. The probability of a future payment is based on assumptions about the person's future mortality which is typically estimated using a life table. Life insurance Whole life insurance pays a pre-determined benefit either at or soon after the insured's death. The symbol ''(x)'' is used to denote "a life aged ''x''" where ''x'' is a non-random parameter that is assumed to be greater than zero. The actuarial present value of one unit of whole life insurance issued to ''(x)'' is denoted by the symbol \,A_x or \,\overline_x in actuarial notation. Let ''G>0'' (the "age at death") be the random variable that models the age at which an individual, such as ''(x)'', will die. And le ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Continuous Annuity
Continuity or continuous may refer to: Mathematics * Continuity (mathematics), the opposing concept to discreteness; common examples include ** Continuous probability distribution or random variable in probability and statistics ** Continuous game, a generalization of games used in game theory ** Law of continuity, a heuristic principle of Gottfried Leibniz * Continuous function, in particular: ** Continuity (topology), a generalization to functions between topological spaces ** Scott continuity, for functions between posets ** Continuity (set theory), for functions between ordinals ** Continuity (category theory), for functors ** Graph continuity, for payoff functions in game theory * Continuity theorem may refer to one of two results: ** Lévy's continuity theorem, on random variables ** Kolmogorov continuity theorem, on stochastic processes * In geometry: ** Parametric continuity, for parametrised curves ** Geometric continuity, a concept primarily applied to the conic s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Life Annuity
A life annuity is an annuity, or series of payments at fixed intervals, paid while the purchaser (or annuitant) is alive. The majority of life annuities are insurance products sold or issued by life insurance companies. However, substantial case law indicates that annuity products are not necessarily insurance products. Annuities can be purchased to provide an income during retirement, or originate from a ''structured settlement'' of a personal injury lawsuit. Life annuities may be sold in exchange for the immediate payment of a lump sum (single-payment annuity) or a series of regular payments (flexible payment annuity), prior to the onset of the annuity. The payment stream from the issuer to the annuitant has an unknown duration based principally upon the date of death of the annuitant. At this point the contract will terminate and the remainder of the fund accumulated is forfeited unless there are other annuitants or beneficiaries in the contract. Thus a life annuity is a for ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Beneficiary
A beneficiary in the broadest sense is a natural person or other legal entity who receives money or other benefits from a benefactor. For example, the beneficiary of a life insurance policy is the person who receives the payment of the amount of insurance after the death of the insured. In trust law, beneficiaries are also known as '' cestui que use''. Most beneficiaries may be designed to designate where the assets will go when the owner(s) dies. However, if the primary beneficiary or beneficiaries are not alive or do not qualify under the restrictions, the assets will probably pass to the ''contingent beneficiaries''. Other restrictions such as being married or more creative ones can be used by a benefactor to attempt to control the behavior of the beneficiaries. Some situations such as retirement accounts do not allow any restrictions beyond the death of the primary beneficiaries, but trusts allow any restrictions that are not illegal or for an illegal purpose. The concept o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Annuity (European Financial Arrangements)
In investment, an annuity is a series of payments made at equal intervals based on a contract with a lump sum of money. Insurance companies are common annuity providers and are used by clients for things like retirement or death benefits. Examples of annuities are regular deposits to a savings account, monthly home mortgage payments, monthly insurance payments and pension payments. Annuities can be classified by the frequency of payment dates. The payments (deposits) may be made weekly, monthly, quarterly, yearly, or at any other regular interval of time. Annuities may be calculated by mathematical functions known as "annuity functions". An annuity which provides for payments for the remainder of a person's lifetime is a life annuity. An annuity which continues indefinitely is a perpetuity. Types Annuities may be classified in several ways. Timing of payments Payments of an ''annuity-immediate'' are made at the end of payment periods, so that interest accrues between the is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Linear Interpolation
In mathematics, linear interpolation is a method of curve fitting using linear polynomials to construct new data points within the range of a discrete set of known data points. Linear interpolation between two known points If the two known points are given by the coordinates (x_0,y_0) and the linear interpolant is the straight line between these points. For a value x in the interval the value y along the straight line is given from the equation of slopes \frac = \frac, which can be derived geometrically from the figure on the right. It is a special case of polynomial interpolation with Solving this equation for y, which is the unknown value at x, gives \begin y &= y_0 + (x-x_0)\frac \\ &= \frac + \frac\\ &= \frac \\ &= \frac, \end which is the formula for linear interpolation in the interval Outside this interval, the formula is identical to linear extrapolation. This formula can also be understood as a weighted average. The weights are inversely related to the dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
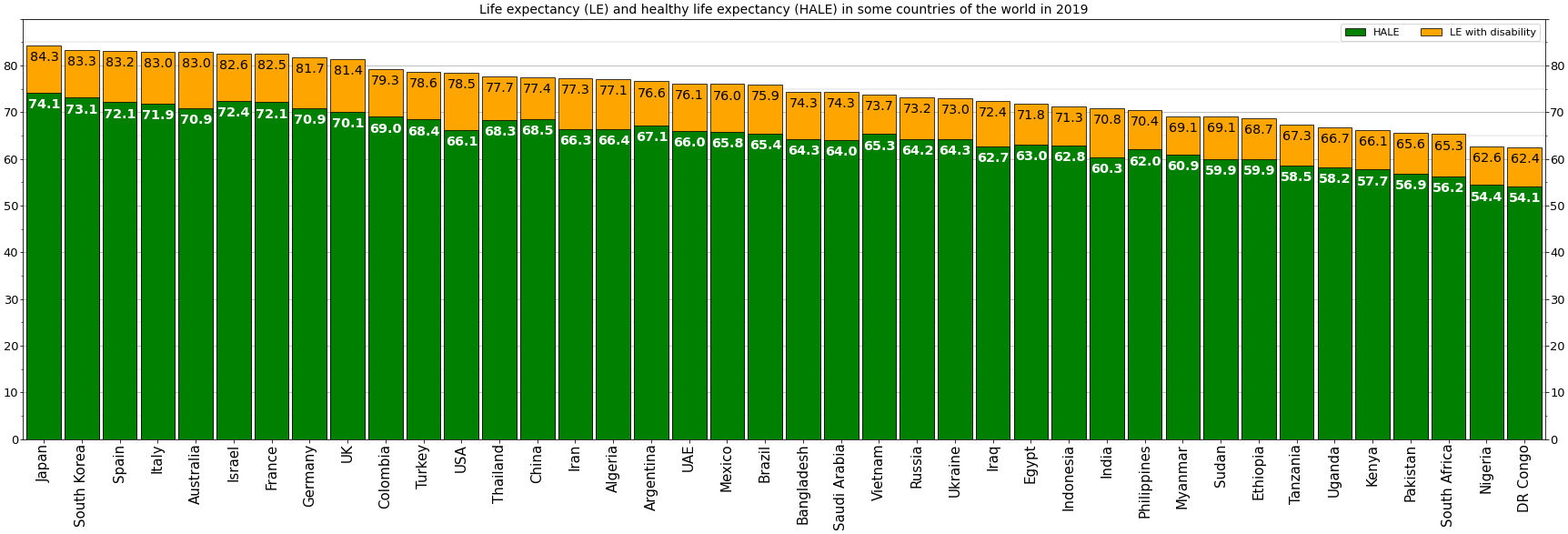
Life Expectancy
Human life expectancy is a statistical measure of the estimate of the average remaining years of life at a given age. The most commonly used measure is ''life expectancy at birth'' (LEB, or in demographic notation ''e''0, where ''e''x denotes the average life remaining at age ''x''). This can be defined in two ways. ''Cohort'' LEB is the mean length of life of a birth Cohort (statistics), cohort (in this case, all individuals born in a given year) and can be computed only for cohorts born so long ago that all their members have died. ''Period'' LEB is the mean length of life of a hypothetical cohort assumed to be exposed, from birth through death, to the mortality rates observed at a given year. National LEB figures reported by national agencies and international organizations for human populations are estimates of ''period'' LEB. Human remains from the early Bronze Age indicate an LEB of 24. In 2019, world LEB was 73.3. A combination of high infant mortality and d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |