|
Abel's Test
In mathematics, Abel's test (also known as Abel's criterion) is a method of testing for the convergence of an infinite series. The test is named after mathematician Niels Henrik Abel, who proved it in 1826. There are two slightly different versions of Abel's test – one is used with series of real numbers, and the other is used with power series in complex analysis. Abel's uniform convergence test is a criterion for the uniform convergence of a series of functions dependent on parameters. Abel's test in real analysis Suppose the following statements are true: # \sum a_n is a convergent series, # b_n is a monotone sequence, and # b_n is bounded. Then \sum a_nb_n is also convergent. It is important to understand that this test is mainly pertinent and useful in the context of non absolutely convergent series \sum a_n. For absolutely convergent series, this theorem, albeit true, is almost self evident. This theorem can be proved directly using summation by parts. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Radius Of Convergence
In mathematics, the radius of convergence of a power series is the radius of the largest Disk (mathematics), disk at the Power series, center of the series in which the series Convergent series, converges. It is either a non-negative real number or \infty. When it is positive, the power series absolute convergence, converges absolutely and compact convergence, uniformly on compact sets inside the open disk of radius equal to the radius of convergence, and it is the Taylor series of the analytic function to which it converges. In case of multiple singularities of a function (singularities are those values of the argument for which the function is not defined), the radius of convergence is the shortest or minimum of all the respective distances (which are all non-negative numbers) calculated from the center of the disk of convergence to the respective singularities of the function. Definition For a power series ''f'' defined as: :f(z) = \sum_^\infty c_n (z-a)^n, where *''a'' is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Addison-Wesley
Addison–Wesley is an American publisher of textbooks and computer literature. It is an imprint of Pearson plc, a global publishing and education company. In addition to publishing books, Addison–Wesley also distributes its technical titles through the O'Reilly Online Learning e-reference service. Addison–Wesley's majority of sales derive from the United States (55%) and Europe (22%). The Addison–Wesley Professional Imprint produces content including books, eBooks, and video for the professional IT worker including developers, programmers, managers, system administrators. Classic titles include '' The Art of Computer Programming'', '' The C++ Programming Language'', '' The Mythical Man-Month'', and '' Design Patterns''. History Lew Addison Cummings and Melbourne Wesley Cummings founded Addison–Wesley in 1942, with the first book published by Addison–Wesley being Massachusetts Institute of Technology professor Francis Weston Sears' ''Mechanics''. Its first comput ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a small variation of the argument induces a small variation of the value of the function. This implies there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Until the 19th century, mathematicians largely relied on intuitive notions of continuity and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the most general continuous functions, and their d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniformly Bounded
In mathematics, a uniformly bounded family of functions is a family of bounded functions that can all be bounded by the same constant. This constant is larger than or equal to the absolute value of any value of any of the functions in the family. Definition Real line and complex plane Let :\mathcal F=\ be a family of functions indexed by I, where X is an arbitrary set and \mathbb is either the set of real \mathbb or complex numbers \mathbb. We call \mathcal F uniformly bounded if there exists a real number M>0 such that :, f_i(x), \le M \ , \qquad \forall i \in I \ , \quad \forall x \in X. Another way of stating this would be the following: :\sup\limits_ \sup\limits_ , f_i(x), \le M. Metric space In general let Y be a metric space with metric d, then the set :\mathcal F=\ is called uniformly bounded if there exists an element a from Y and a real number M such that :d(f_i(x), a) \leq M \qquad \forall i \in I \quad \forall x \in X. Examples * Every uniformly converge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
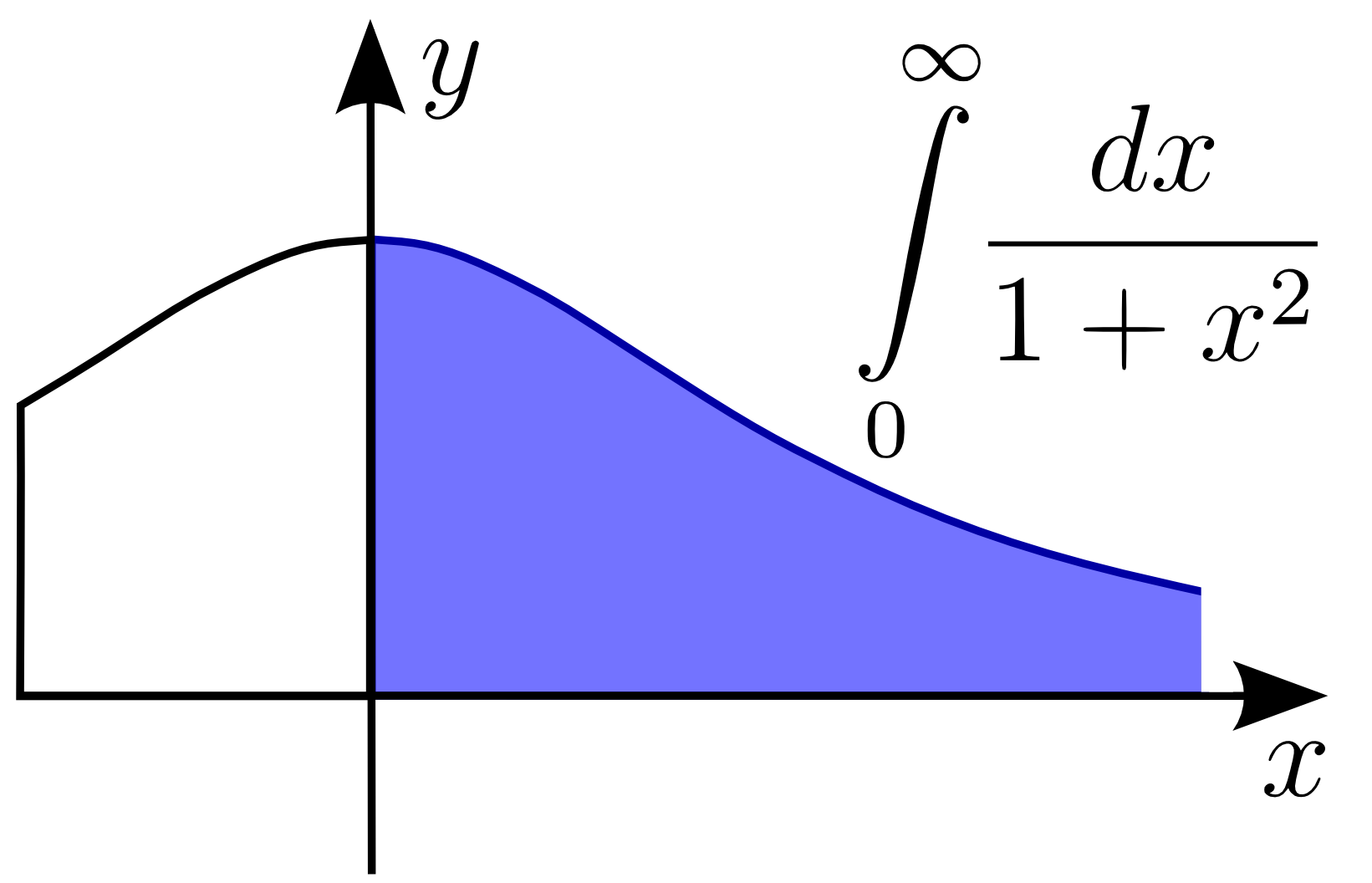
Improper Integral
In mathematical analysis, an improper integral is an extension of the notion of a definite integral to cases that violate the usual assumptions for that kind of integral. In the context of Riemann integrals (or, equivalently, Darboux integrals), this typically involves unboundedness, either of the set over which the integral is taken or of the integrand (the function being integrated), or both. It may also involve bounded but not closed sets or bounded but not continuous functions. While an improper integral is typically written symbolically just like a standard definite integral, it actually represents a limit of a definite integral or a sum of such limits; thus improper integrals are said to converge or diverge. If a regular definite integral (which may retronymically be called a proper integral) is worked out as if it is improper, the same answer will result. In the simplest case of a real-valued function of a single variable integrated in the sense of Riemann (or Darbou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dirichlet's Test
In mathematics, Dirichlet's test is a method of testing for the convergence of a series that is especially useful for proving conditional convergence. It is named after its author Peter Gustav Lejeune Dirichlet, and was published posthumously in the '' Journal de Mathématiques Pures et Appliquées'' in 1862. Statement The test states that if (a_n) is a monotonic sequence of real numbers with \lim_ a_n = 0 and (b_n) is a sequence of real numbers or complex numbers with bounded partial sums, then the series :\sum_^ a_n b_n converges. Proof Let S_n = \sum_^n a_k b_k and B_n = \sum_^n b_k. From summation by parts, we have that S_n = a_ B_n + \sum_^ B_k (a_k - a_). Since the magnitudes of the partial sums B_n are bounded by some ''M'' and a_n \to 0 as n\to\infty, the first of these terms approaches zero: , a_ B_n, \leq , a_ M, \to 0 as n\to\infty. Furthermore, for each ''k'', , B_k (a_k - a_), \leq M, a_k - a_, . Since (a_n) is monotone, it is either decreasing or in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alternating Series Test
In mathematical analysis, the alternating series test proves that an alternating series is convergent when its terms decrease monotonically in absolute value and approach zero in the limit. The test was devised by Gottfried Leibniz and is sometimes known as Leibniz's test, Leibniz's rule, or the Leibniz criterion. The test is only sufficient, not necessary, so some convergent alternating series may fail the first part of the test. For a generalization, see Dirichlet's test. History Leibniz discussed the criterion in his unpublished ''De quadratura arithmetica'' of 1676 and shared his result with Jakob Hermann in June 1705 and with Johann Bernoulli in October, 1713. It was only formally published in 1993. Formal statement Alternating series test A series of the form \sum_^\infty (-1)^ a_n = a_0-a_1 + a_2 - a_3 + \cdots where either all ''a''''n'' are positive or all ''a''''n'' are negative, is called an alternating series. The alternating series test guarantees that ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Euclidean plane. In topology, it is often denoted as because it is a one-dimensional unit -sphere. If is a point on the unit circle's circumference, then and are the lengths of the legs of a right triangle whose hypotenuse has length 1. Thus, by the Pythagorean theorem, and satisfy the equation x^2 + y^2 = 1. Since for all , and since the reflection of any point on the unit circle about the - or -axis is also on the unit circle, the above equation holds for all points on the unit circle, not only those in the first quadrant. The interior of the unit circle is called the open unit disk, while the interior of the unit circle combined with the unit circle itself is called the closed unit disk. One may also use other notions of "dis ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Summation By Parts
In mathematics, summation by parts transforms the summation of products of sequences into other summations, often simplifying the computation or (especially) estimation of certain types of sums. It is also called Abel's lemma or Abel transformation, named after Niels Henrik Abel who introduced it in 1826. Statement Suppose \ and \ are two sequences. Then, :\sum_^n f_k(g_-g_k) = \left(f_g_ - f_m g_m\right) - \sum_^n g_(f_- f_). Using the forward difference operator \Delta, it can be stated more succinctly as :\sum_^n f_k\Delta g_k = \left(f_ g_ - f_m g_m\right) - \sum_^ g_\Delta f_k, Summation by parts is an analogue to integration by parts: :\int f\,dg = f g - \int g\,df, or to Abel's summation formula: :\sum_^n f(k)(g_-g_)= \left(f(n)g_ - f(m) g_m\right) - \int_^n g_ f'(t) dt. An alternative statement is :f_n g_n - f_m g_m = \sum_^ f_k\Delta g_k + \sum_^ g_k\Delta f_k + \sum_^ \Delta f_k \Delta g_k which is analogous to the integration by parts formula for semimartingales ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergent Series
In mathematics, a series is the sum of the terms of an infinite sequence of numbers. More precisely, an infinite sequence (a_1, a_2, a_3, \ldots) defines a series that is denoted :S=a_1 + a_2 + a_3 + \cdots=\sum_^\infty a_k. The th partial sum is the sum of the first terms of the sequence; that is, :S_n = a_1 +a_2 + \cdots + a_n = \sum_^n a_k. A series is convergent (or converges) if and only if the sequence (S_1, S_2, S_3, \dots) of its partial sums tends to a limit; that means that, when adding one a_k after the other ''in the order given by the indices'', one gets partial sums that become closer and closer to a given number. More precisely, a series converges, if and only if there exists a number \ell such that for every arbitrarily small positive number \varepsilon, there is a (sufficiently large) integer N such that for all n \ge N, :\left , S_n - \ell \right , 1 produce a convergent series: *: ++++++\cdots = . * Alternating the signs of reciprocals of powers o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parameter
A parameter (), generally, is any characteristic that can help in defining or classifying a particular system (meaning an event, project, object, situation, etc.). That is, a parameter is an element of a system that is useful, or critical, when identifying the system, or when evaluating its performance, status, condition, etc. ''Parameter'' has more specific meanings within various disciplines, including mathematics, computer programming, engineering, statistics, logic, linguistics, and electronic musical composition. In addition to its technical uses, there are also extended uses, especially in non-scientific contexts, where it is used to mean defining characteristics or boundaries, as in the phrases 'test parameters' or 'game play parameters'. Modelization When a system theory, system is modeled by equations, the values that describe the system are called ''parameters''. For example, in mechanics, the masses, the dimensions and shapes (for solid bodies), the densities and t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |