|
A List Of Production Functions
This is a list of production functions that have been used in the economics literature. Production functions are a key part of modelling national output and national income. For a much more extensive discussion of various types of production functions and their properties, their relationships and origin, see Chambers (1988) and Sickles and Zelenyuk (2019, Chapter 6). The production functions listed below, and their properties are shown for the case of two factors of production, capital (K), and labor (L), mostly for heuristic purposes. These functions and their properties are easily generalizable to include additional factors of production (like land, natural resources, entrepreneurship, etc.) Technology There are three common ways to incorporate technology (or the efficiency with which factors of production are used) into a production function (here ''A'' is a scale factor, ''F'' is a production function, and ''Y'' is the amount of physical output produced): * Hicks-neutr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Production Function
In economics, a production function gives the technological relation between quantities of physical inputs and quantities of output of goods. The production function is one of the key concepts of mainstream economics, mainstream neoclassical economics, neoclassical theories, used to define marginal product and to distinguish allocative efficiency, a key focus of economics. One important purpose of the production function is to address allocative efficiency in the use of factor inputs in production and the resulting distribution of income to those factors, while abstracting away from the technological problems of achieving technical efficiency, as an engineer or professional manager might understand it. For modelling the case of many outputs and many inputs, researchers often use the so-called Shephard's distance functions or, alternatively, directional distance functions, which are generalizations of the simple production function in economics. In macroeconomics, aggregate produc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Constant Elasticity Of Substitution
Constant elasticity of substitution (CES) is a common specification of many production functions and utility function In economics, utility is a measure of a certain person's satisfaction from a certain state of the world. Over time, the term has been used with at least two meanings. * In a Normative economics, normative context, utility refers to a goal or ob ...s in neoclassical economics. CES holds that the ability to substitute one input factor with another (for example labour with capital) to maintain the same level of production stays constant over different production levels. For utility functions, CES means the consumer has constant preferences of how they would like to substitute different goods (for example labour with consumption) while keeping the same level of utility, for all levels of utility. What this means is that both producers and consumers have similar input structures and preferences no matter the level of output or utility. The vital economic element o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shephard's Lemma
Shephard's lemma is a result in microeconomics having applications in the theory of the firm and in consumer choice. The lemma states that if indifference curves of the expenditure or cost function are convex, then the cost-minimizing point of a given good (i) with price p_i is unique. The idea is that a consumer will buy a unique ideal amount of each item to minimize the price for obtaining a certain level of utility given the price of goods in the market. The lemma is named after Ronald Shephard, who proved it using the distance formula in his book ''Theory of Cost and Production Functions'' in 1953. The equivalent result in the context of consumer theory was first derived by Lionel W. McKenzie in 1957. It states that the partial derivatives of the expenditure function with respect to the prices of goods equal the Hicksian demand functions for the relevant goods. Similar results had already been derived by John Hicks (1939) and Paul Samuelson (1947). Definition In consumer ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Ozaki Cost Function
In economics the generalized-Ozaki (GO) cost function is a general description of the cost of production proposed by Shinichiro Nakamura. The GO cost function is notable for explicitly considering nonhomothetic technology, where the proportions of inputs can vary as the output changes. This stands in contrast to the standard production model, which assumes homothetic technology. The GO function For a given output y, at time t and a vector of m input prices p_i, the generalized-Ozaki (GO) cost function C() is expressed as Here, b_=b_ and \sum_i b_=1, i,j=1,..,m. By applying the Shephard's lemma, we derive the demand function for input i, x_i : The GO cost function is flexible in the price space, and treats scale effects and technical change in a highly general manner. The concavity condition which ensures that a constant function aligns with cost minimization for a specific set of p, necessitates that its Hessian (the matrix of second partial derivatives with respect to p_i and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stone–Geary Utility Function
The Stone–Geary utility function takes the form U = \prod_ (q_i-\gamma_i)^ where U is utility, q_i is consumption of good i, and \beta and \gamma are parameters. For \gamma_i = 0, the Stone–Geary function reduces to the generalised Cobb–Douglas function. The Stone–Geary utility function gives rise to the Linear Expenditure System. In case of \sum_i \beta_i =1 the demand function equals q_i = \gamma_i + \frac (y - \sum_j \gamma_j p_j) where y is total expenditure, and p_i is the price of good i. The Stone–Geary utility function was first derived by Roy C. Geary, in a comment on earlier work by Lawrence Klein and Herman Rubin. Richard Stone Sir John Richard Nicholas Stone (30 August 1913 – 6 December 1991) was an eminent British economist. He was educated at Gonville and Caius College and King's College at the University of Cambridge. In 1984, he was awarded the Nobel Memori ... was the first to estimate the Linear Expenditure System. References Further r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Leontief Production Function
In economics, the Leontief production function or fixed proportions production function is a production function that implies the factors of production which will be used in fixed (technologically predetermined) proportions, as there is no substitutability between factors. It was named after Wassily Leontief and represents a limiting case of the constant elasticity of substitution production function. For the simple case of a good that is produced with two inputs, the function is of the form :q = \text\left(\frac,\frac\right) where ''q'' is the quantity of output produced, ''z''1 and ''z''2 are the utilised quantities of input 1 and input 2 respectively, and ''a'' and ''b'' are technologically determined constants. Example Suppose that the intermediate goods "tires" and "steering wheels" are used in the production of automobiles (for simplicity of the example, to the exclusion of anything else). Then in the above formula ''q'' refers to the number of automobiles produced, ''z ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
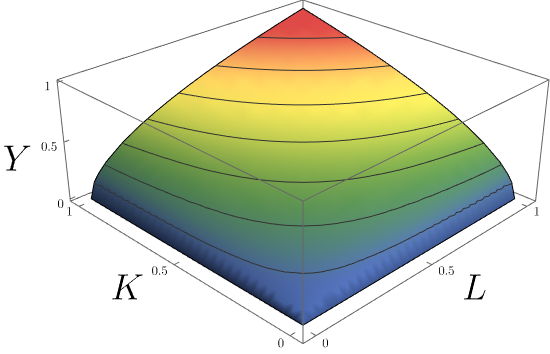
Cobb–Douglas Production Function
In economics and econometrics, the Cobb–Douglas production function is a particular functional form of the production function, widely used to represent the technological relationship between the amounts of two or more inputs (particularly physical capital and labor) and the amount of output that can be produced by those inputs. The Cobb–Douglas form was developed and tested against statistical evidence by Charles Cobb and Paul Douglas between 1927 and 1947; according to Douglas, the functional form itself was developed earlier by Philip Wicksteed. Formulation In its most standard form for production of a single good with two factors, the function is given by: : Y(L,K)=AL^\beta K^\alpha where: * ''Y'' = total production (the real value of all goods produced in a year or 365.25 days) * ''L'' = labour input (person-hours worked in a year or 365.25 days) * ''K'' = capital input (a measure of all machinery, equipment, and buildings; the value of capital input divided by th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Returns To Scale
In economics, the concept of returns to scale arises in the context of a firm's production function. It explains the long-run linkage of increase in output (production) relative to associated increases in the inputs (factors of production). In the long run, all factors of production are variable and subject to change in response to a given increase in production scale. In other words, returns to scale analysis is a long-term theory because a company can only change the scale of production in the long run by changing factors of production, such as building new facilities, investing in new machinery, or improving technology. There are three possible types of returns to scale: * If output increases by the same proportional change as all inputs change then there are constant returns to scale (CRS). For example, when inputs (labor and capital) increase by 100%, output increases by 100%. * If output increases by less than the proportional change in all inputs, there are decreasing retu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Economics
Economics () is a behavioral science that studies the Production (economics), production, distribution (economics), distribution, and Consumption (economics), consumption of goods and services. Economics focuses on the behaviour and interactions of Agent (economics), economic agents and how economy, economies work. Microeconomics analyses what is viewed as basic elements within economy, economies, including individual agents and market (economics), markets, their interactions, and the outcomes of interactions. Individual agents may include, for example, households, firms, buyers, and sellers. Macroeconomics analyses economies as systems where production, distribution, consumption, savings, and Expenditure, investment expenditure interact; and the factors of production affecting them, such as: Labour (human activity), labour, Capital (economics), capital, Land (economics), land, and Entrepreneurship, enterprise, inflation, economic growth, and public policies that impact gloss ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
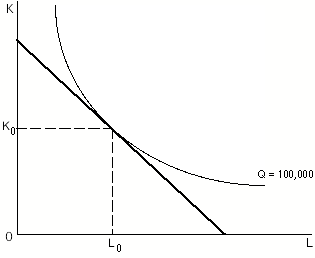
Isoquant
An isoquant (derived from ''quantity'' and the Greek word ', , meaning "equal"), in microeconomics, is a contour line drawn through the set of points at which the same quantity of output is produced while changing the quantities of two or more inputs. The x and y axis on an isoquant represent two relevant inputs, which are usually a factor of production such as labour, capital, land, or organisation. An isoquant may also be known as an "iso-product curve", or an "equal product curve". Vs. indifference curves While an indifference curve mapping helps to solve the utility-maximizing problem of consumers, the isoquant mapping deals with the cost-minimization and profit and output maximisation problem of producers. Indifference curves further differ to isoquants, in that they cannot offer a precise measurement of utility, only how it is relevant to a baseline. Whereas, from an isoquant, the product can be measured accurately in physical units, and it is known by exactly how much iso ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |