|
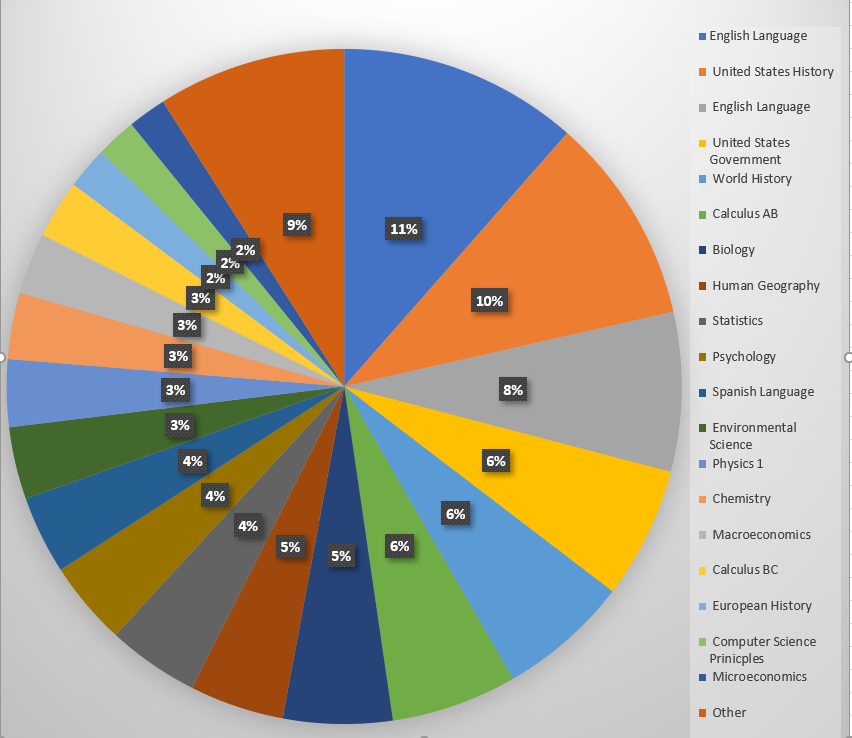
AP Calculus
Advanced Placement (AP) Calculus (also known as AP Calc, Calc AB / BC, AB / BC Calc or simply AB / BC) is a set of two distinct Advanced Placement calculus courses and exams offered by the American nonprofit organization College Board. AP Calculus AB covers basic introductions to limits, derivatives, and integrals. AP Calculus BC covers all AP Calculus AB topics plus integration by parts, infinite series, parametric equations, vector calculus, and polar coordinate functions, among other topics. AP Calculus AB AP Calculus AB is an Advanced Placement calculus course. It is traditionally taken after precalculus and is the first calculus course offered at most schools except for possibly a regular or honors calculus class. The Pre-Advanced Placement pathway for math helps prepare students for further Advanced Placement classes and exams. Purpose According to the College Board: Topic outline The material includes the study and application of differentiation and integration, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Advanced Placement
Advanced Placement (AP) is a program in the United States and Canada created by the College Board. AP offers undergraduate university-level curricula and examinations to high school students. Colleges and universities in the US and elsewhere may grant placement and course credit to students who obtain qualifying scores on the examinations. The AP curriculum for each of the various subjects is created for the College Board by a panel of experts and college-level educators in that academic discipline. For a high school course to have the designation as offering an AP course, the course must be audited by the College Board to ascertain that it satisfies the AP curriculum as specified in the Board's Course and Examination Description (CED). If the course is approved, the school may use the AP designation and the course will be publicly listed on the AP Course Ledger. History 20th century After the end of World War II, the Ford Foundation created a fund that supported committees ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Differential Calculus
In mathematics, differential calculus is a subfield of calculus that studies the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus—the study of the area beneath a curve. The primary objects of study in differential calculus are the derivative of a Function (mathematics), function, related notions such as the Differential of a function, differential, and their applications. The derivative of a function at a chosen input value describes the Rate (mathematics)#Of_change, rate of change of the function near that input value. The process of finding a derivative is called differentiation. Geometrically, the derivative at a point is the slope of the tangent, tangent line to the graph of a function, graph of the function at that point, provided that the derivative exists and is defined at that point. For a real-valued function of a single real variable, the derivative of a function at a point generally determines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
Arc length is the distance between two points along a section of a curve. Development of a formulation of arc length suitable for applications to mathematics and the sciences is a problem in vector calculus and in differential geometry. In the most basic formulation of arc length for a vector valued curve (thought of as the trajectory of a particle), the arc length is obtained by integrating speed, the magnitude of the velocity vector over the curve with respect to time. Thus the length of a continuously differentiable curve (x(t),y(t)), for a\le t\le b, in the Euclidean plane is given as the integral L = \int_a^b \sqrt\,dt, (because \sqrt is the magnitude of the velocity vector (x'(t),y'(t)), i.e., the particle's speed). The defining integral of arc length does not always have a closed-form expression, and numerical integration may be used instead to obtain numerical values of arc length. Determining the length of an irregular arc segment by approximating the arc segment as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polar Coordinate System
In mathematics, the polar coordinate system specifies a given point in a plane by using a distance and an angle as its two coordinates. These are *the point's distance from a reference point called the ''pole'', and *the point's direction from the pole relative to the direction of the ''polar axis'', a ray drawn from the pole. The distance from the pole is called the ''radial coordinate'', ''radial distance'' or simply ''radius'', and the angle is called the ''angular coordinate'', ''polar angle'', or ''azimuth''. The pole is analogous to the origin in a Cartesian coordinate system. Polar coordinates are most appropriate in any context where the phenomenon being considered is inherently tied to direction and length from a center point in a plane, such as spirals. Planar physical systems with bodies moving around a central point, or phenomena originating from a central point, are often simpler and more intuitive to model using polar coordinates. The polar coordinate system i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parametric Equation
In mathematics, a parametric equation expresses several quantities, such as the coordinates of a point (mathematics), point, as Function (mathematics), functions of one or several variable (mathematics), variables called parameters. In the case of a single parameter, parametric equations are commonly used to express the trajectory of a moving point, in which case, the parameter is often, but not necessarily, time, and the point describes a curve, called a parametric curve. In the case of two parameters, the point describes a Surface (mathematics), surface, called a parametric surface. In all cases, the equations are collectively called a parametric representation, or parametric system, or parameterization (also spelled parametrization, parametrisation) of the object. For example, the equations \begin x &= \cos t \\ y &= \sin t \end form a parametric representation of the unit circle, where is the parameter: A point is on the unit circle if and only if there is a value of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Taylor Series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor series are equal near this point. Taylor series are named after Brook Taylor, who introduced them in 1715. A Taylor series is also called a Maclaurin series when 0 is the point where the derivatives are considered, after Colin Maclaurin, who made extensive use of this special case of Taylor series in the 18th century. The partial sum formed by the first terms of a Taylor series is a polynomial of degree that is called the th Taylor polynomial of the function. Taylor polynomials are approximations of a function, which become generally more accurate as increases. Taylor's theorem gives quantitative estimates on the error introduced by the use of such approximations. If the Taylor series of a function is convergent, its sum is the limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convergence Tests
In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series \sum_^\infty a_n. List of tests Limit of the summand If the limit of the summand is undefined or nonzero, that is \lim_a_n \ne 0, then the series must diverge. In this sense, the partial sums are Cauchy only if this limit exists and is equal to zero. The test is inconclusive if the limit of the summand is zero. This is also known as the nth-term test, test for divergence, or the divergence test. Ratio test This is also known as d'Alembert's criterion. : Consider two limits \ell=\liminf_\left, \frac\ and L=\limsup_\left, \frac\. If \ell>1, the series diverges. If L 1. The case of p = 1, k = 1 yields the harmonic series, which diverges. The case of p = 2, k = 1 is the Basel problem and the series converges to \frac. In general, for p > 1, k = 1, the series is equal to the Riemann zeta funct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multivariable Calculus
Multivariable calculus (also known as multivariate calculus) is the extension of calculus in one variable to calculus with functions of several variables: the differentiation and integration of functions involving multiple variables ('' multivariate''), rather than just one. Multivariable calculus may be thought of as an elementary part of calculus on Euclidean space. The special case of calculus in three dimensional space is often called ''vector calculus''. Introduction In single-variable calculus, operations like differentiation and integration are made to functions of a single variable. In multivariate calculus, it is required to generalize these to multiple variables, and the domain is therefore multi-dimensional. Care is therefore required in these generalizations, because of two key differences between 1D and higher dimensional spaces: # There are infinite ways to approach a single point in higher dimensions, as opposed to two (from the positive and negative direct ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Separation Of Variables
In mathematics, separation of variables (also known as the Fourier method) is any of several methods for solving ordinary differential equation, ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation. Ordinary differential equations (ODE) A differential equation for the unknown f(x) is separable if it can be written in the form :\frac f(x) = g(x)h(f(x)) where g and h are given functions. This is perhaps more transparent when written using y = f(x) as: :\frac=g(x)h(y). So now as long as ''h''(''y'') ≠ 0, we can rearrange terms to obtain: : = g(x) \, dx, where the two variables ''x'' and ''y'' have been separated. Note ''dx'' (and ''dy'') can be viewed, at a simple level, as just a convenient notation, which provides a handy mnemonic aid for assisting with manipulations. A formal definition of ''dx'' as a differential (infinitesimal) is somewhat advanced. Al ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
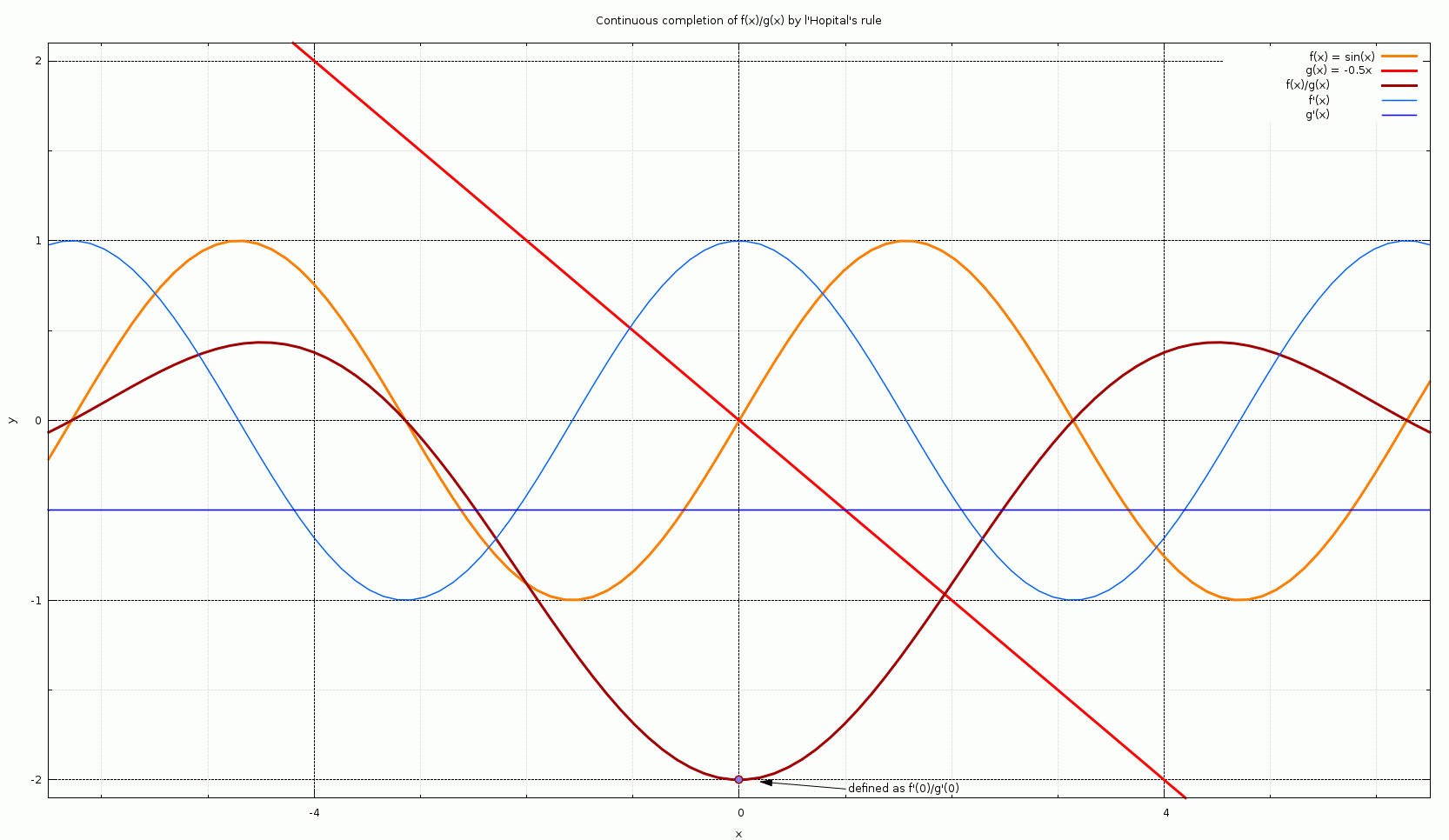
L'Hôpital's Rule
L'Hôpital's rule (, ), also known as Bernoulli's rule, is a mathematical theorem that allows evaluating limits of indeterminate forms using derivatives. Application (or repeated application) of the rule often converts an indeterminate form to an expression that can be easily evaluated by substitution. The rule is named after the 17th-century French mathematician Guillaume de l'Hôpital. Although the rule is often attributed to de l'Hôpital, the theorem was first introduced to him in 1694 by the Swiss mathematician Johann Bernoulli. L'Hôpital's rule states that for functions and which are defined on an open interval and differentiable on I\setminus \ for a (possibly infinite) accumulation point of , if \lim \limits_f(x)=\lim \limits_g(x)=0 \text\pm\infty, and g'(x)\ne 0 for all in I\setminus \, and \lim \limits_\frac exists, then :\lim_\frac = \lim_\frac. The differentiation of the numerator and denominator often simplifies the quotient or converts it to a limit t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a continuous function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically as . The process of solving for antiderivatives is called antidifferentiation (or indefinite integration), and its opposite operation is called ''differentiation'', which is the process of finding a derivative. Antiderivatives are often denoted by capital Roman letters such as and . Antiderivatives are related to definite integrals through the second fundamental theorem of calculus: the definite integral of a function over a closed interval where the function is Riemann integrable is equal to the difference between the values of an antiderivative evaluated at the endpoints of the interval. In physics, antiderivatives arise in the context of rectilinear motion (e.g., in explaining the relationship between position, veloc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fundamental Theorem Of Calculus
The fundamental theorem of calculus is a theorem that links the concept of derivative, differentiating a function (mathematics), function (calculating its slopes, or rate of change at every point on its domain) with the concept of integral, integrating a function (calculating the area under its graph, or the cumulative effect of small contributions). Roughly speaking, the two operations can be thought of as inverses of each other. The first part of the theorem, the first fundamental theorem of calculus, states that for a continuous function , an antiderivative or indefinite integral can be obtained as the integral of over an interval with a variable upper bound. Conversely, the second part of the theorem, the second fundamental theorem of calculus, states that the integral of a function over a fixed Interval (mathematics), interval is equal to the change of any antiderivative between the ends of the interval. This greatly simplifies the calculation of a definite integral pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |