|
A. Pieyre De Mandiargues
A is the first letter of the Latin and English alphabet. A may also refer to: Science and technology Quantities and units * ''a'', a measure for the attraction between particles in the Van der Waals equation * ''A'' value, a measure of substituent effects on the stereochemistry of cyclohexane * absorbance (''A'') * acceleration (''a'') * activity (chemistry) (''a'') * adsorption (a) * annum (a), for year * are (a), a unit of area (equal to 100 square metres; redirects to ''hectare'') * atto- (a-), the SI prefix meaning 10−18 * Ampere (A), unit of electric current * ångström (Å) a unit of length (equal to 1 metres) * area (''A'') * attenuation coefficient (''a'') * Bohr radius (''a''0) * chemical affinity (''A'') * gain (electronics) (''A'') * Hall coefficient (''A''H) * Hamaker constant (''A'') * Helmholtz free energy (''A'') * Hyperfine coupling constant (''a'' or ''A'') * magnetic vector potential (''A'') * mass number of a nuclide (''A'') * pr ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hall Coefficient
The Hall effect is the production of a voltage difference (the Hall voltage) across an electrical conductor that is transverse to an electric current in the conductor and to an applied magnetic field perpendicular to the current. It was discovered by Edwin Hall in 1879. A Hall effect can also occur across a void or hole in a semiconductor or metal plate, when current is injected via contacts that lie on the boundary or edge of the void or hole, and the charge flows outside the void or hole, in the metal or semiconductor. This Hall effect becomes observable in a perpendicular applied magnetic field across voltage contacts that lie on the boundary of the void on either side of a line connecting the current contacts. It exhibits apparent sign reversal in comparison to the standard "ordinary Hall effect" in the simply connected specimen, and depends only on the current injected from within the void. Superposition may also be realized in the Hall effect: first imagine the standard ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
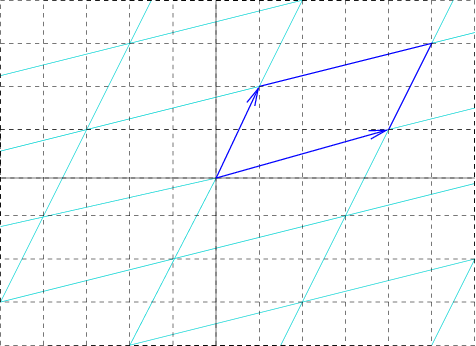
Unit Cell Length
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessarily have unit size, or even a particular size at all. Rather, the primitive cell is the closest analogy to a unit vector, since it has a determined size for a given lattice and is the basic building block from which larger cells are constructed. The concept is used particularly in describing crystal structure in two and three dimensions, though it makes sense in all dimensions. A lattice can be characterized by the geometry of its unit cell, which is a section of the tiling (a parallelogram or parallelepiped) that generates the whole tiling using only translations. There are two special cases of the unit cell: the primitive cell and the conventional cell. The primitive cell is a unit cell corresponding to a single lattice point, it is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Diffusivity
In heat transfer analysis, thermal diffusivity is the thermal conductivity divided by density and specific heat capacity at constant pressure. It measures the rate of transfer of heat of a material from the hot end to the cold end. It has the SI derived unit of m2/s. Thermal diffusivity is usually denoted by lowercase alpha (), but , , ( kappa), , and are also used. The formula is: :\alpha = \frac where * is thermal conductivity (W/(m·K)) * is specific heat capacity (J/(kg·K)) * is density (kg/m3) Together, can be considered the volumetric heat capacity (J/(m3·K)). As seen in the heat equation, :\frac = \alpha \nabla^2 T, one way to view thermal diffusivity is as the ratio of the time derivative of temperature to its curvature, quantifying the rate at which temperature concavity is "smoothed out". In a sense, thermal diffusivity is a contrasting measure to thermal inertia. In a substance with high thermal diffusivity, heat moves rapidly through it because the substa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Specific Surface Area
Specific surface area (SSA) is a property of solids defined as the total surface area of a material per unit of mass, (with units of m2/kg or m2/g) or solid or bulk volume (units of m2/m3 or m−1). It is a physical value that can be used to determine the type and properties of a material (e.g. soil or snow). It has a particular importance for adsorption, heterogeneous catalysis, and reactions on surfaces. Measurement Values obtained for specific surface area depend on the method of measurement. In adsorption based methods, the size of the adsorbate molecule (the probe molecule), the exposed crystallographic planes at the surface and measurement temperature all affect the obtained specific surface area. For this reason, in addition to the most commonly used Brunauer–Emmett–Teller (N2-BET) adsorption method, several techniques have been developed to measure the specific surface area of particulate materials at ambient temperatures and at controllable scales, including methy ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Rotational Constant
In rotordynamics, the rigid rotor is a mechanical model of rotating systems. An arbitrary rigid rotor is a 3-dimensional rigid object, such as a top. To orient such an object in space requires three angles, known as Euler angles. A special rigid rotor is the ''linear rotor'' requiring only two angles to describe, for example of a diatomic molecule. More general molecules are 3-dimensional, such as water (asymmetric rotor), ammonia (symmetric rotor), or methane (spherical rotor). Linear rotor The linear rigid rotor model consists of two point masses located at fixed distances from their center of mass. The fixed distance between the two masses and the values of the masses are the only characteristics of the rigid model. However, for many actual diatomics this model is too restrictive since distances are usually not completely fixed. Corrections on the rigid model can be made to compensate for small variations in the distance. Even in such a case the rigid rotor model is a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Richardson's Constant
Thermionic emission is the liberation of electrons from an electrode by virtue of its temperature (releasing of energy supplied by heat). This occurs because the thermal energy given to the charge carrier overcomes the work function of the material. The charge carriers can be electrons or ions, and in older literature are sometimes referred to as thermions. After emission, a charge that is equal in magnitude and opposite in sign to the total charge emitted is initially left behind in the emitting region. But if the emitter is connected to a battery, the charge left behind is neutralized by charge supplied by the battery as the emitted charge carriers move away from the emitter, and finally the emitter will be in the same state as it was before emission. The classical example of thermionic emission is that of electrons from a hot cathode into a vacuum (also known as thermal electron emission or the Edison effect) in a vacuum tube. The hot cathode can be a metal filament, a coated ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relative Atomic Mass
Relative atomic mass (symbol: ''A''; sometimes abbreviated RAM or r.a.m.), also known by the deprecated synonym atomic weight, is a dimensionless physical quantity defined as the ratio of the average mass of atoms of a chemical element in a given sample to the atomic mass constant. The atomic mass constant (symbol: ''m'') is defined as being of the mass of a carbon-12 atom. Since both quantities in the ratio are masses, the resulting value is dimensionless; hence the value is said to be ''relative''. For a single given sample, the relative atomic mass of a given element is the weighted arithmetic mean of the masses of the individual atoms (including their isotopes) that are present in the sample. This quantity can vary substantially between samples because the sample's origin (and therefore its radioactive history or diffusion history) may have produced unique combinations of isotopic abundances. For example, due to a different mixture of stable carbon-12 and carbon-13 isoto ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reciprocal Lattice Vector
In physics, the reciprocal lattice represents the Fourier transform of another lattice (group) (usually a Bravais lattice). In normal usage, the initial lattice (whose transform is represented by the reciprocal lattice) is a periodic spatial function in real space known as the ''direct lattice''. While the direct lattice exists in real space and is commonly understood to be a physical lattice (such as the lattice of a crystal), the reciprocal lattice exists in the space of spatial frequencies known as reciprocal space or k space, where \mathbf refers to the wavevector. In quantum physics, reciprocal space is closely related to momentum space according to the proportionality \mathbf = \hbar \mathbf, where \mathbf is the momentum vector and \hbar is the Planck constant. The reciprocal lattice of a reciprocal lattice is equivalent to the original direct lattice, because the defining equations are symmetrical with respect to the vectors in real and reciprocal space. Mathematically ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pre-exponential Factor
In chemical kinetics, the pre-exponential factor or A factor is the pre-exponential constant in the Arrhenius equation#Equation, Arrhenius equation (equation shown below), an empirical relationship between temperature and Reaction rate constant, rate coefficient. It is usually designated by A when determined from experiment, while Z is usually left for collision frequency. The pre-exponential factor can be thought of as a measure of the frequency of properly oriented collisions. It is typically determined experimentally by measuring the rate constant k at a particular temperature and fitting the data to the Arrhenius equation. The pre-exponential factor is generally not exactly constant, but rather depends on the specific reaction being studied and the temperature at which the reaction is occurring. A=\frac The units of the pre-exponential factor A are identical to those of the rate constant and will vary depending on the order of the reaction. For a first-order reaction, it has ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mass Number
The mass number (symbol ''A'', from the German word ''Atomgewicht'' tomic weight, also called atomic mass number or nucleon number, is the total number of protons and neutrons (together known as nucleons) in an atomic nucleus. It is approximately equal to the ''atomic'' (also known as ''isotopic'') mass of the atom expressed in atomic mass units. Since protons and neutrons are both baryons, the mass number ''A'' is identical with the baryon number ''B'' of the nucleus (and also of the whole atom or ion). The mass number is different for each isotope of a given chemical element, and the difference between the mass number and the atomic number ''Z'' gives the number of neutrons (''N'') in the nucleus: . The mass number is written either after the element name or as a superscript to the left of an element's symbol. For example, the most common isotope of carbon is carbon-12, or , which has 6 protons and 6 neutrons. The full isotope symbol would also have the atomic number ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Magnetic Vector Potential
In classical electromagnetism, magnetic vector potential (often called A) is the vector quantity defined so that its curl is equal to the magnetic field: \nabla \times \mathbf = \mathbf. Together with the electric potential ''φ'', the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials ''φ'' and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields. Magnetic vector potential was first introduced by Franz Ernst Neumann and Wilhelm Eduard Weber in 1845 and in 1846, respectively. Lord Kelvin also introduced vector potential in 1847, along with the formula relating it to the magnetic field. Magnetic vector potential The magnetic vector potential A is a vector field, defined along with the electric potential ''ϕ'' (a scalar field) by the equations: \mathbf = \n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |