|
6th Battalion 18th Field Artillery Regiment (United States)
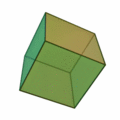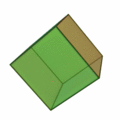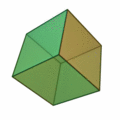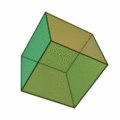
6 (six) is the natural number following 5 and preceding 7. It is a composite number and the smallest perfect number. In mathematics Six is the smallest positive integer which is neither a square number nor a prime number; it is the second smallest composite number, behind 4; its proper divisors are , and . Since 6 equals the sum of its proper divisors, it is a perfect number; 6 is the smallest of the perfect numbers. It is also the smallest Granville number, or \mathcal-perfect number. As a perfect number: *6 is related to the Mersenne prime 3, since . (The next perfect number is 28.) *6 is the only even perfect number that is not the sum of successive odd cubes. *6 is the root of the 6-aliquot tree, and is itself the aliquot sum of only one other number; the square number, . Six is the only number that is both the sum and the product of three consecutive positive numbers. Unrelated to 6's being a perfect number, a Golomb ruler of length 6 is a "perfect ruler". Six is a co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Senary
A senary () numeral system (also known as base-6, heximal, or seximal) has six as its base. It has been adopted independently by a small number of cultures. Like decimal, it is a semiprime, though it is unique as the product of the only two consecutive numbers that are both prime (2 and 3). As six is a superior highly composite number, many of the arguments made in favor of the duodecimal system also apply to senary. In turn, the senary logic refers to an extension of Jan Łukasiewicz's and Stephen Cole Kleene's ternary logic systems adjusted to explain the logic of statistical tests and missing data patterns in sciences using empirical methods. Formal definition The standard set of digits in senary is given by \mathcal_6 = \lbrace 0, 1, 2, 3, 4, 5\rbrace, with a linear order 0 < 1 < 2 < 3 < 4 < 5. Let be the |
Khmer Numerals
Khmer numerals are the numerals used in the Khmer language. They have been in use since at least the early 7th century, with the earliest known use being on a stele dated to AD 604 found in Prasat Bayang, near Angkor Borei, Cambodia. Numerals Having been derived from the Hindu numerals, modern Khmer numerals also represent a decimal positional notation system. It is the script with the first extant material evidence of zero as a numerical figure, dating its use back to the seventh century, two centuries before its certain use in India. Old Khmer, or Angkorian Khmer, also possessed separate symbols for the numbers 10, 20, and 100. Each multiple of 20 or 100 would require an additional stroke over the character, so the number 47 was constructed using the 20 symbol with an additional upper stroke, followed by the symbol for number 7. This inconsistency with its decimal system suggests that spoken Angkorian Khmer used a vigesimal system. As both Thai and Lao scripts ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mersenne Prime
In mathematics, a Mersenne prime is a prime number that is one less than a power of two. That is, it is a prime number of the form for some integer . They are named after Marin Mersenne, a French Minim friar, who studied them in the early 17th century. If is a composite number then so is . Therefore, an equivalent definition of the Mersenne primes is that they are the prime numbers of the form for some prime . The exponents which give Mersenne primes are 2, 3, 5, 7, 13, 17, 19, 31, ... and the resulting Mersenne primes are 3, 7, 31, 127, 8191, 131071, 524287, 2147483647, ... . Numbers of the form without the primality requirement may be called Mersenne numbers. Sometimes, however, Mersenne numbers are defined to have the additional requirement that be prime. The smallest composite Mersenne number with prime exponent ''n'' is . Mersenne primes were studied in antiquity because of their close connection to perfect numbers: the Euclid–Euler theorem as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |