|
5040 (number)
5040 is a factorial (7!), a superior highly composite number, abundant number, colossally abundant number and the number of permutations of 4 items out of 10 choices (10 × 9 × 8 × 7 = 5040). It is also one less than a square, making (7, 71) a Brown number pair. Philosophy Plato mentions in his ''Laws (dialogue), Laws'' that 5040 is a convenient number to use for division (mathematics), dividing many things (including both the citizens and the land of a city-state or ''polis'') into lesser parts, making it an ideal number for the number of citizens (heads of families) making up a ''polis''. He remarks that this number can be divided by all the natural numbers, (natural) numbers from 1 (number), 1 to 12 (number), 12 with the single exception of 11 (number), 11 (however, it is not the smallest number to have this property; 2520 (number), 2520 is). He rectifies this "defect" by suggesting that two families could be subtracted from the citizen body to produce the number 5038, which i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Factorial
In mathematics, the factorial of a non-negative denoted is the product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial: \begin n! &= n \times (n-1) \times (n-2) \times (n-3) \times \cdots \times 3 \times 2 \times 1 \\ &= n\times(n-1)!\\ \end For example, 5! = 5\times 4! = 5 \times 4 \times 3 \times 2 \times 1 = 120. The value of 0! is 1, according to the convention for an empty product. Factorials have been discovered in several ancient cultures, notably in Indian mathematics in the canonical works of Jain literature, and by Jewish mystics in the Talmudic book '' Sefer Yetzirah''. The factorial operation is encountered in many areas of mathematics, notably in combinatorics, where its most basic use counts the possible distinct sequences – the permutations – of n distinct objects: there In mathematical analysis, factorials are used in power series for the exponential function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
2520 (number)
2520 (two thousand five hundred twenty) is the natural number following 2519 and preceding 2521. In mathematics 2520 is: *the smallest number divisible by all integers from 1 to 10, i.e., it is their least common multiple. *half of 7! ( 5040), meaning 7 factorial, or 1×2×3×4×5×6×7. *the product of five consecutive numbers, namely 3×4×5×6×7. *a superior highly composite number. *a colossally abundant number. *the last highly composite number which is half of the next highly composite number. *the last highly composite number that is a divisor of all following highly composite numbers. *palindromic in bases 11 (199111), and a repdigit in bases 55, 59 and 62. *a Harshad number in bases 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16. *the aliquot sum of 1080. *part of the 53-aliquot tree. The complete aliquot sequence starting at 1080 is: 1080, 2520, 6840, 16560, 41472, 82311, 27441, 12209, 451, 53, 1, 0. Factors The factors, also called divisor In mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathworld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at Urbana–Champaign. History Eric W. Weisstein, the creator of the site, was a physics and astronomy student who got into the habit of writing notes on his mathematical readings. In 1995 he put his notes online and called it "Eric's Treasure Trove of Mathematics." It contained hundreds of pages/articles, covering a wide range of mathematical topics. The site became popular as an extensive single resource on mathematics on the web. Weisstein continuously improved the notes and accepted corrections and comments from online readers. In 1998, he made a contract with CRC Press and the contents of the site were published in print and CD-ROM form, titled "CRC Concise Encyclopedia of Mathematic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
40320 (number)
40,000 (forty thousand) is the natural number that comes after 39,999 and before 40,001. It is the square of 200. Selected numbers in the range 40001–49999 40001 to 40999 * 40320 = smallest factorial (8!) that is not a highly composite number * 40425 = square pyramidal number * 40585 = largest factorion * 40678 = pentagonal pyramidal number * 40804 = palindromic square 41000 to 41999 * 41041 = Carmichael number * 41472 = 3-smooth number * 41586 = Large Schröder number * 41616 = triangular square number * 41835 = Motzkin number * 41841 = 1/41841 = 0.0000239 is a repeating decimal with period 7. 42000 to 42999 * 42680 = octahedral number * 42875 = 353 * 42925 = square pyramidal number 43000 to 43999 * 43261 = Markov number * 43390 = number of primes \leq 2^. * 43560 = pentagonal pyramidal number * 43691 = Wagstaff prime * 43777 = smallest member of a prime sextuplet 44000 to 44999 * 44044 = palindrome of 79 after 6 iterations of the "reverse and add" iterative process ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Hypothesis
In mathematics, the Riemann hypothesis is the conjecture that the Riemann zeta function has its zeros only at the negative even integers and complex numbers with real part . Many consider it to be the most important unsolved problem in pure mathematics. It is of great interest in number theory because it implies results about the distribution of prime numbers. It was proposed by , after whom it is named. The Riemann hypothesis and some of its generalizations, along with Goldbach's conjecture and the twin prime conjecture, make up Hilbert's eighth problem in David Hilbert's list of twenty-three unsolved problems; it is also one of the Clay Mathematics Institute's Millennium Prize Problems, which offers a million dollars to anyone who solves any of them. The name is also used for some closely related analogues, such as the Riemann hypothesis for curves over finite fields. The Riemann zeta function ζ(''s'') is a function whose argument ''s'' may be any complex numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
If And Only If
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false. The connective is biconditional (a statement of material equivalence), and can be likened to the standard material conditional ("only if", equal to "if ... then") combined with its reverse ("if"); hence the name. The result is that the truth of either one of the connected statements requires the truth of the other (i.e. either both statements are true, or both are false), though it is controversial whether the connective thus defined is properly rendered by the English "if and only if"—with its pre-existing meaning. For example, ''P if and only if Q'' means that ''P'' is true whenever ''Q'' is true, and the only case in which ''P'' is true is if ''Q'' is also true, whereas in the case of ''P if Q'', there could be other scenarios where ''P'' is true and ''Q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Limit (mathematics)
In mathematics, a limit is the value that a function (or sequence) approaches as the input (or index) approaches some value. Limits are essential to calculus and mathematical analysis, and are used to define continuity, derivatives, and integrals. The concept of a limit of a sequence is further generalized to the concept of a limit of a topological net, and is closely related to limit and direct limit in category theory. In formulas, a limit of a function is usually written as : \lim_ f(x) = L, (although a few authors may use "Lt" instead of "lim") and is read as "the limit of of as approaches equals ". The fact that a function approaches the limit as approaches is sometimes denoted by a right arrow (→ or \rightarrow), as in :f(x) \to L \text x \to c, which reads "f of x tends to L as x tends to c". History Grégoire de Saint-Vincent gave the first definition of limit (terminus) of a geometric series in his work ''Opus Geometricum'' (1647): "The ''terminus'' of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Inequality (mathematics)
In mathematics, an inequality is a relation which makes a non-equal comparison between two numbers or other mathematical expressions. It is used most often to compare two numbers on the number line by their size. There are several different notations used to represent different kinds of inequalities: * The notation ''a'' ''b'' means that ''a'' is greater than ''b''. In either case, ''a'' is not equal to ''b''. These relations are known as strict inequalities, meaning that ''a'' is strictly less than or strictly greater than ''b''. Equivalence is excluded. In contrast to strict inequalities, there are two types of inequality relations that are not strict: * The notation ''a'' ≤ ''b'' or ''a'' ⩽ ''b'' means that ''a'' is less than or equal to ''b'' (or, equivalently, at most ''b'', or not greater than ''b''). * The notation ''a'' ≥ ''b'' or ''a'' ⩾ ''b'' means that ''a'' is greater than or equal to ''b'' (or, equivalently, at least ''b'', or not less than ''b''). The r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
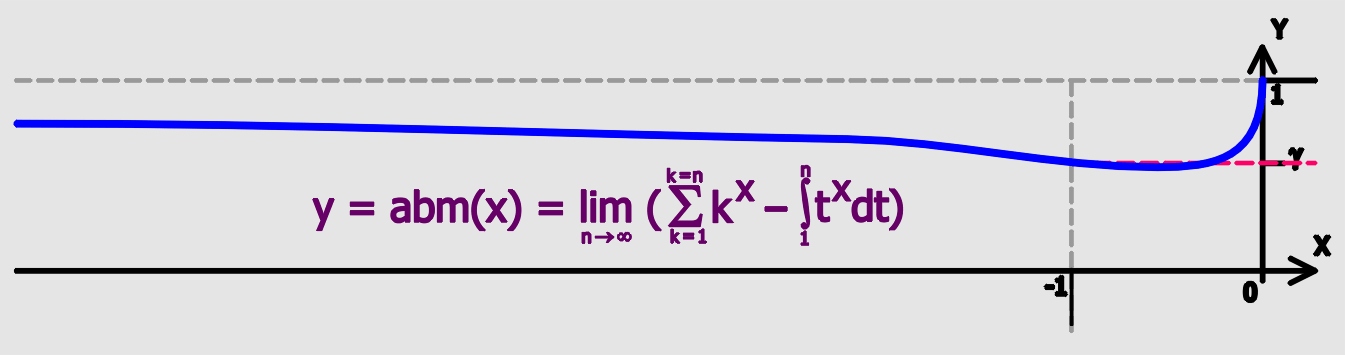
Euler–Mascheroni Constant
Euler's constant (sometimes also called the Euler–Mascheroni constant) is a mathematical constant usually denoted by the lowercase Greek letter gamma (). It is defined as the limiting difference between the harmonic series and the natural logarithm, denoted here by \log: :\begin \gamma &= \lim_\left(-\log n + \sum_^n \frac1\right)\\ px&=\int_1^\infty\left(-\frac1x+\frac1\right)\,dx. \end Here, \lfloor x\rfloor represents the floor function. The numerical value of Euler's constant, to 50 decimal places, is: : History The constant first appeared in a 1734 paper by the Swiss mathematician Leonhard Euler, titled ''De Progressionibus harmonicis observationes'' (Eneström Index 43). Euler used the notations and for the constant. In 1790, Italian mathematician Lorenzo Mascheroni used the notations and for the constant. The notation appears nowhere in the writings of either Euler or Mascheroni, and was chosen at a later time perhaps because of the constant's connecti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Divisor Function
In mathematics, and specifically in number theory, a divisor function is an arithmetic function related to the divisors of an integer. When referred to as ''the'' divisor function, it counts the ''number of divisors of an integer'' (including 1 and the number itself). It appears in a number of remarkable identities, including relationships on the Riemann zeta function and the Eisenstein series of modular forms. Divisor functions were studied by Ramanujan, who gave a number of important congruences and identities; these are treated separately in the article Ramanujan's sum. A related function is the divisor summatory function, which, as the name implies, is a sum over the divisor function. Definition The sum of positive divisors function σ''z''(''n''), for a real or complex number ''z'', is defined as the sum of the ''z''th powers of the positive divisors of ''n''. It can be expressed in sigma notation as :\sigma_z(n)=\sum_ d^z\,\! , where is shorthand for "''d' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Highly Composite Number
__FORCETOC__ A highly composite number is a positive integer with more divisors than any smaller positive integer has. The related concept of largely composite number refers to a positive integer which has at least as many divisors as any smaller positive integer. The name can be somewhat misleading, as the first two highly composite numbers (1 and 2) are not actually composite numbers; however, all further terms are. The late mathematician Jean-Pierre Kahane has suggested that Plato must have known about highly composite numbers as he deliberately chose 5040 as the ideal number of citizens in a city as 5040 has more divisors than any numbers less than it. Ramanujan wrote and titled his paper on the subject in 1915. Examples The initial or smallest 38 highly composite numbers are listed in the table below . The number of divisors is given in the column labeled ''d''(''n''). Asterisks indicate superior highly composite numbers. The divisors of the first 15 highly composite ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Jean-Pierre Kahane
Jean-Pierre Kahane (11 December 1926 – 21 June 2017) was a French mathematician with contributions to harmonic analysis. Career Kahane attended the École normale supérieure and obtained the ''agrégation'' of mathematics in 1949. He then worked for the CNRS from 1949 to 1954, first as an intern and then as a research assistant. He defended his PhD in 1954; his advisor was Szolem Mandelbrojt. He was assistant professor, then professor of mathematics in Montpellier from 1954 to 1961. Since then, he has been professor until his retirement in 1994, then professor emeritus at the Université de Paris-Sud in Orsay. He was a Plenary Speaker at the International Congress of Mathematicians in 1962 in Stockholm and an Invited Speaker at the 1986 ICM meeting in Berkeley, California. He was elected corresponding member of the French Academy of Sciences in 1982 and full member in 1998. He was president of the Société mathématique de France, the French Mathematical Society from 1971 to ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |