|
34 Equal Temperament
In musical theory, 34 equal temperament, also referred to as 34-TET, 34-EDO or 34-ET, is the tempered tuning derived by dividing the octave into 34 equal-sized steps (equal frequency ratios). Each step represents a frequency ratio of , or 35.29 cents . History and use Unlike divisions of the octave into 19, 31 or 53 steps, which can be considered as being derived from ancient Greek intervals (the greater and lesser diesis and the syntonic comma), division into 34 steps did not arise 'naturally' out of older music theory, although Cyriakus Schneegass proposed a meantone system with 34 divisions based in effect on half a chromatic semitone (the difference between a major third and a minor third, 25:24 or 70.67 cents). Wider interest in the tuning was not seen until modern times, when the computer made possible a systematic search of all possible equal temperaments. While Barbour discusses it,''Tuning and Temperament'', Michigan State College Press, 1951 the first recognition of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Equal Division Of The Octave
An equal temperament is a musical temperament or tuning system, which approximates just intervals by dividing an octave (or other interval) into equal steps. This means the ratio of the frequencies of any adjacent pair of notes is the same, which gives an equal perceived step size as pitch is perceived roughly as the logarithm of frequency. In classical music and Western music in general, the most common tuning system since the 18th century has been twelve-tone equal temperament (also known as 12 equal temperament, 12-TET or 12-ET; informally abbreviated to twelve equal), which divides the octave into 12 parts, all of which are equal on a logarithmic scale, with a ratio equal to the 12th root of 2 ( ≈ 1.05946). That resulting smallest interval, the width of an octave, is called a semitone or half step. In Western countries the term ''equal temperament'', without qualification, generally means 12-TET. In modern times, 12-TET is usually tuned relative to a standard pitch o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Modulation (music)
In music, modulation is the change from one tonality ( tonic, or tonal center) to another. This may or may not be accompanied by a change in key signature (a key change). Modulations articulate or create the structure or form of many pieces, as well as add interest. Treatment of a chord as the tonic for less than a phrase is considered tonicization. Requirements * Harmonic: quasi- tonic, modulating dominant, pivot chordForte (1979), p. 267. * Melodic: recognizable segment of the scale of the quasi-tonic or strategically placed leading-tone * Metric and rhythmic: quasi-tonic and modulating dominant on metrically accented beats, prominent pivot chord The quasi-tonic is the tonic of the new key established by the modulation was semi. The modulating dominant is the dominant of the quasi-tonic. The pivot chord is a predominant to the modulating dominant and a chord common to both the keys of the tonic and the quasi-tonic. For example, in a modulation to the dominant, ii/V– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Septimal Sixth-tone
A septimal 1/3-tone (in music) is an interval with the ratio of 28:27, which is the difference between the perfect fourth and the supermajor third. It is about 62.96 cents wide. The septimal 1/3-tone can be viewed either as a musical interval in its own right, or as a comma; if it is tempered out in a given tuning system, the distinction between these two intervals is lost. The septimal 1/3-tone may be derived from the harmonic series as the interval between the twenty-seventh and twenty-eighth harmonics. It may be considered a diesis. The septimal 1/3-tone, along with the septimal diesis is tempered out by five-tone equal temperament, and equal temperaments which divide the octave into a small multiple of 5 steps, such as 15-TET and 25-TET. This family of scales is known as Blackwood temperament in honor of Easley Blackwood, Jr., who first analyzed 10-note subsets of 15-TET that take advantage of the temperament. When added to the 15:14 semitone, the 21:20 semitone and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Chromatic Semitone
In modern Western tonal music theory an augmented unison or augmented prime is the interval between two notes on the same staff position, or denoted by the same note letter, whose alterations cause them, in ordinary equal temperament, to be one semitone apart. In other words, it is a unison where one note has been altered by a half-step, such as B and B or C and C. The interval is often described as a chromatic semitone. The term, in its French form ''unisson superflu'', appears to have been coined by Jean-Philippe Rameau in 1722, who also called this interval a minor semitone (''semiton mineur'').Gene Henry Anderson, "Musical Terminology in J.-P. Rameau's ''Traité de l'harmonie'': A Study and Glossary Based on an Index". PhD diss. (Iowa City: University of Iowa, 1981): 196. Historically, this interval, like the tritone, is described as being "mi contra fa", and therefore is the "diabolus in musica" (the Devil in music). In 12-tone equal temperament, it is the enharmonic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
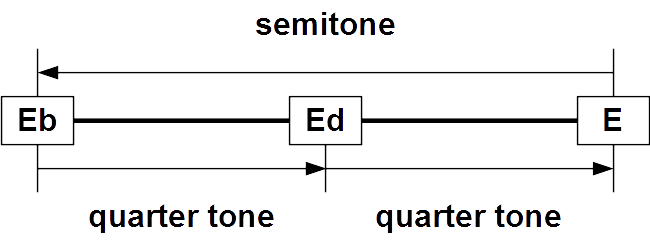
Diatonic Semitone
A semitone, also called a half step or a half tone, is the smallest musical interval commonly used in Western tonal music, and it is considered the most dissonant when sounded harmonically. It is defined as the interval between two adjacent notes in a 12-tone scale. For example, C is adjacent to C; the interval between them is a semitone. In a 12-note approximately equally divided scale, any interval can be defined in terms of an appropriate number of semitones (e.g. a whole tone or major second is 2 semitones wide, a major third 4 semitones, and a perfect fifth 7 semitones. In music theory, a distinction is made between a diatonic semitone, or minor second (an interval encompassing two different staff positions, e.g. from C to D) and a chromatic semitone or augmented unison (an interval between two notes at the same staff position, e.g. from C to C). These are enharmonically equivalent when twelve-tone equal temperament is used, but are not the same thing in meantone ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Neutral Second
In music theory, a neutral interval is an interval that is neither a major nor minor, but instead in between. For example, in equal temperament, a major third is 400 cents, a minor third is 300 cents, and a neutral third is 350 cents. A neutral interval inverts to a neutral interval. For example, the inverse of a neutral third is a neutral sixth. Roughly, neutral intervals are a quarter tone sharp from minor intervals and a quarter tone flat from major intervals. In just intonation, as well as in tunings such as 31-ET, 41-ET, or 72-ET, which more closely approximate just intonation, the intervals are closer together. * Neutral second * Neutral third * Neutral sixth * Neutral seventh Second A neutral second or medium second is an interval wider than a minor second and narrower than a major second. Three distinct intervals may be termed neutral seconds: * The intermediate neutral second, called the lesser undecimal neutral second , has a ratio between the higher-frequ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Septimal Whole Tone
In music, the septimal whole tone, septimal major second, or supermajor second is the musical interval exactly or approximately equal to an 8/7 ratio of frequencies.Andrew Horner, Lydia Ayres (2002). ''Cooking with Csound: Woodwind and Brass Recipes'', p.131. . "Super-Major Second". It is about 231 cents wide in just intonation.Leta E. Miller, Fredric Lieberman (2006). ''Lou Harrison'', p.72. . 24 equal temperament does not match this interval particularly well, its nearest representation being at 250 cents, approximately 19 cents sharp. The septimal whole tone may be derived from the harmonic series as the interval between the seventh and eighth harmonics and the term ''septimal'' refers to the fact that it utilizes the seventh harmonic. It can also be thought of as the octave inversion of the 7/4 interval, the harmonic seventh. No close approximation to this interval exists in the standard 12 equal temperament used in most modern western music. The very simple 5 equa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Septimal Minor Third
In music, the septimal minor third, also called the subminor third (e.g., by Ellis), is the musical interval exactly or approximately equal to a 7/6 ratio of frequencies. In terms of cents, it is 267 cents, a quartertone of size 36/35 flatter than a just minor third of 6/5. In 24-tone equal temperament five quarter tones approximate the septimal minor third at 250 cents (). A septimal minor third is almost exactly two-ninths of an octave, and thus all divisions of the octave into multiples of nine (72 equal temperament being the most notable) have an almost perfect match to this interval. The septimal major sixth, 12/7, is the inverse of this interval. The septimal minor third may be derived in the harmonic series from the seventh harmonic, and as such is in inharmonic ratios with all notes in the regular 12TET scale, with the exception of the fundamental and the octave. It has a darker but generally pleasing character when compared to the 6/5 third. A triad formed by using ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Neutral Third
A neutral third is a musical interval wider than a minor third but narrower than a major third , named by Jan Pieter Land in 1880. Land makes reference to the neutral third attributed to Zalzal (8th c.), described by Al-Farabi (10th c.) as corresponding to a ratio of 27:22 (354.5 cents) and by Avicenna (Ibn Sina, 11th c.) as 39:32 (342.5 cents). The Zalzalian third may have been a mobile interval. Three distinct intervals may be termed neutral thirds: * The ''undecimal neutral third'' has a ratio of 11:9 between the frequencies of the two tones, or about 347.41 cents . This ratio is the mathematical mediant of the major third 5/4 and the minor third 6/5, and as such, has the property that if harmonic notes of frequency ''f'' and (11/9) ''f'' are played together, the beat frequency of the 5th harmonic of the lower pitch against the 4th of the upper, i.e. , 5 f - 4 (11/9) f, = (1/9) f, is the same as the beat frequency of the 6th harmonic of the lower pitch against the 5th o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
 |
Septimal Major Third
In music, the septimal major third , also called the supermajor third (by Hermann von Helmholtz among others Hermann L. F. von Helmholtz (2007). ''Sensations of Tone'', p. 187. .) and sometimes '' Bohlen–Pierce third'' is the musical interval exactly or approximately equal to a just 9:7 ratioAndrew Horner, Lydia Ayres (2002). ''Cooking with Csound: Woodwind and Brass Recipes'', p. 131. . "Super-Major Second". of frequencies, or alternately 14:11. It is equal to 435 cents, sharper than a just major third (5:4) by the septimal quarter tone (36:35) (). In 24-TET the septimal major third is approximated by 9 quarter tones, or 450 cents (). Both 24 and 19 equal temperament map the septimal major third and the septimal narrow fourth (21:16) to the same interval. The septimal major third has a characteristic brassy sound which is much less sweet than a pure major third, but is classed as a 9-limit consonance. Together with the root 1:1 and the perfect fifth of 3:2, it makes up the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
Perfect Fourth
A fourth is a musical interval encompassing four staff positions in the music notation of Western culture, and a perfect fourth () is the fourth spanning five semitones (half steps, or half tones). For example, the ascending interval from C to the next F is a perfect fourth, because the note F is the fifth semitone above C, and there are four staff positions between C and F. Diminished and augmented fourths span the same number of staff positions, but consist of a different number of semitones (four and six, respectively). The perfect fourth may be derived from the harmonic series as the interval between the third and fourth harmonics. The term ''perfect'' identifies this interval as belonging to the group of perfect intervals, so called because they are neither major nor minor. A perfect fourth in just intonation corresponds to a pitch ratio of 4:3, or about 498 cents (), while in equal temperament a perfect fourth is equal to five semitones, or 500 cents (see additive synth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
|
 |
Septimal Tritone
A septimal tritone is a tritone (about one half of an octave) that involves the factor seven. There are two that are inverses. The lesser septimal tritone (also Huygens' tritone) is the musical interval with ratio 7:5 (582.51 cents). The greater septimal tritone (also Euler's tritone), is an interval with ratio 10:7 (617.49 cents). They are also known as the sub-fifth and super-fourth, or subminor fifth and supermajor fourth, respectively. The 7:5 interval (diminished fifth) is equal to a 6:5 minor third plus a 7:6 subminor third. The 10:7 interval (augmented fourth) is equal to a 5:4 major third plus an 8:7 supermajor second, or a 9:7 supermajor third plus a 10:9 major second. The difference between these two is the septimal sixth tone (50:49, 34.98 cents) . 12 equal temperament and 22 equal temperament do not distinguish between these tritones; 19 equal temperament does distinguish them but doesn't match them closely. 31 equal temperament and 41 equal temperament both disti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |