|
3-torus
The three-dimensional torus, or 3-torus, is defined as any topological space that is homeomorphic to the Cartesian product of three circles, \mathbb^3 = S^1 \times S^1 \times S^1. In contrast, the usual torus is the Cartesian product of only two circles. The 3-torus is a three-dimensional compact manifold with no boundary. It can be obtained by "gluing" the three pairs of opposite faces of a cube, where being "glued" can be intuitively understood to mean that when a particle moving in the interior of the cube reaches a point on a face, it goes through it and appears to come forth from the corresponding point on the opposite face, producing periodic boundary conditions. Gluing only one pair of opposite faces produces a solid torus while gluing two of these pairs produces the solid space between two nested tori. In 1984, Alexei Starobinsky and Yakov Borisovich Zel'dovich Yakov Borisovich Zeldovich ( be, Я́каў Бары́савіч Зяльдо́віч, russian: Я́ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
3-Manifold 3-Torus
In mathematics, a 3-manifold is a space that locally looks like Euclidean 3-dimensional space. A 3-manifold can be thought of as a possible shape of the universe. Just as a sphere looks like a plane to a small enough observer, all 3-manifolds look like our universe does to a small enough observer. This is made more precise in the definition below. Introduction Definition A topological space ''X'' is a 3-manifold if it is a second-countable Hausdorff space and if every point in ''X'' has a neighbourhood that is homeomorphic to Euclidean 3-space. Mathematical theory of 3-manifolds The topological, piecewise-linear, and smooth categories are all equivalent in three dimensions, so little distinction is made in whether we are dealing with say, topological 3-manifolds, or smooth 3-manifolds. Phenomena in three dimensions can be strikingly different from phenomena in other dimensions, and so there is a prevalence of very specialized techniques that do not generalize to dimensions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
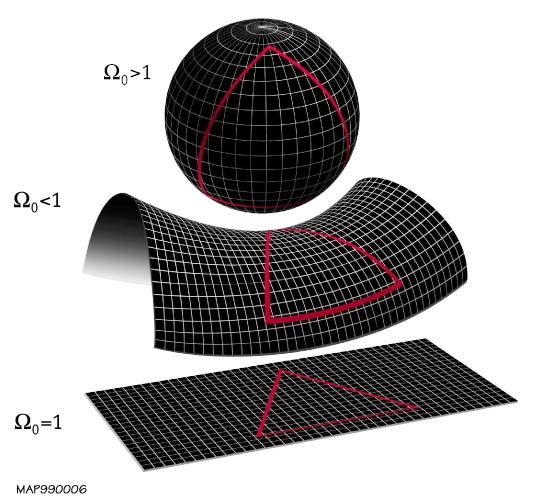
Shape Of The Universe
The shape of the universe, in physical cosmology, is the local and global geometry of the universe. The local features of the geometry of the universe are primarily described by its curvature, whereas the topology of the universe describes general global properties of its shape as a continuous object. The spatial curvature is defined by general relativity, which describes how spacetime is curved due to the effect of gravity. The spatial topology cannot be determined from its curvature, due to the fact that there exist locally indistinguishable spaces that may be endowed with different topological invariants. Cosmologists distinguish between the observable universe and the entire universe, the former being a ball-shaped portion of the latter that can, in principle, be accessible by astronomical observations. Assuming the cosmological principle, the observable universe is similar from all contemporary vantage points, which allows cosmologists to discuss properties of the entire ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Torus
In geometry, a torus (plural tori, colloquially donut or doughnut) is a surface of revolution generated by revolving a circle in three-dimensional space about an axis that is coplanar with the circle. If the axis of revolution does not touch the circle, the surface has a ring shape and is called a torus of revolution. If the axis of revolution is tangent to the circle, the surface is a horn torus. If the axis of revolution passes twice through the circle, the surface is a spindle torus. If the axis of revolution passes through the center of the circle, the surface is a degenerate torus, a double-covered sphere. If the revolved curve is not a circle, the surface is called a ''toroid'', as in a square toroid. Real-world objects that approximate a torus of revolution include swim rings, inner tubes and ringette rings. Eyeglass lenses that combine spherical and cylindrical correction are toric lenses. A torus should not be confused with a '' solid torus'', which is formed by r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cartesian Product
In mathematics, specifically set theory, the Cartesian product of two sets ''A'' and ''B'', denoted ''A''×''B'', is the set of all ordered pairs where ''a'' is in ''A'' and ''b'' is in ''B''. In terms of set-builder notation, that is : A\times B = \. A table can be created by taking the Cartesian product of a set of rows and a set of columns. If the Cartesian product is taken, the cells of the table contain ordered pairs of the form . One can similarly define the Cartesian product of ''n'' sets, also known as an ''n''-fold Cartesian product, which can be represented by an ''n''-dimensional array, where each element is an ''n''-tuple. An ordered pair is a 2-tuple or couple. More generally still, one can define the Cartesian product of an indexed family of sets. The Cartesian product is named after René Descartes, whose formulation of analytic geometry gave rise to the concept, which is further generalized in terms of direct product. Examples A deck of cards An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Compact Space
In mathematics, specifically general topology, compactness is a property that seeks to generalize the notion of a closed and bounded subset of Euclidean space by making precise the idea of a space having no "punctures" or "missing endpoints", i.e. that the space not exclude any ''limiting values'' of points. For example, the open interval (0,1) would not be compact because it excludes the limiting values of 0 and 1, whereas the closed interval ,1would be compact. Similarly, the space of rational numbers \mathbb is not compact, because it has infinitely many "punctures" corresponding to the irrational numbers, and the space of real numbers \mathbb is not compact either, because it excludes the two limiting values +\infty and -\infty. However, the ''extended'' real number line ''would'' be compact, since it contains both infinities. There are many ways to make this heuristic notion precise. These ways usually agree in a metric space, but may not be equivalent in other topologic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates (e.g ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. Viewed from a corner it is a hexagon and its net is usually depicted as a cross. The cube is the only regular hexahedron and is one of the five Platonic solids. It has 6 faces, 12 edges, and 8 vertices. The cube is also a square parallelepiped, an equilateral cuboid and a right rhombohedron a 3-zonohedron. It is a regular square prism in three orientations, and a trigonal trapezohedron in four orientations. The cube is dual to the octahedron. It has cubical or octahedral symmetry. The cube is the only convex polyhedron whose faces are all squares. Orthogonal projections The ''cube'' has four special orthogonal projections, centered, on a vertex, edges, face and normal to its vertex figure. The first and third correspond to the A2 and B2 Coxeter planes. Spherical tiling The cube can also be represented as a spherical tiling, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Periodic Boundary Conditions
Periodic boundary conditions (PBCs) are a set of boundary conditions which are often chosen for approximating a large (infinite) system by using a small part called a ''unit cell''. PBCs are often used in computer simulations and mathematical models. The topology of two-dimensional PBC is equal to that of a ''world map'' of some video games; the geometry of the unit cell satisfies perfect two-dimensional tiling, and when an object passes through one side of the unit cell, it re-appears on the opposite side with the same velocity. In topological terms, the space made by two-dimensional PBCs can be thought of as being mapped onto a torus (compactification). The large systems approximated by PBCs consist of an infinite number of unit cells. In computer simulations, one of these is the original simulation box, and others are copies called ''images''. During the simulation, only the properties of the original simulation box need to be recorded and propagated. The ''minimum-image conventi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solid Torus
In mathematics, a solid torus is the topological space formed by sweeping a disk around a circle. It is homeomorphic to the Cartesian product S^1 \times D^2 of the disk and the circle, endowed with the product topology. A standard way to visualize a solid torus is as a toroid, embedded in 3-space. However, it should be distinguished from a torus, which has the same visual appearance: the torus is the two-dimensional space on the boundary of a toroid, while the solid torus includes also the compact interior space enclosed by the torus. Topological properties The solid torus is a connected, compact, orientable 3-dimensional manifold with boundary. The boundary is homeomorphic to S^1 \times S^1, the ordinary torus. Since the disk D^2 is contractible, the solid torus has the homotopy type of a circle, S^1.. Therefore the fundamental group and homology groups are isomorphic to those of the circle: \begin \pi_1\left(S^1 \times D^2\right) &\cong \pi_1\left(S^1\right) \cong \mathbb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Alexei Starobinsky
Alexei Alexandrovich Starobinsky (russian: Алексе́й Алекса́ндрович Староби́нский; born 19 April 1948) is a Soviet and Russian astrophysicist and cosmologist. He received the Kavli Prize in Astrophysics "for pioneering the theory of cosmic inflation", together with Alan Guth and Andrei Linde in 2014. Early life Starobinsky is a former student of Yakov Zeldovich at Moscow State University from where he earned a bachelor's degree in 1972. In 1975, he earned a PhD degree from the Landau Institute for Theoretical Physics of the Russian Academy of Sciences and is now a senior scientist at the institute. From 1990 to 1997, he headed the department of gravitation and cosmology and, from 1999 to 2003, he was the institute's deputy director. In the 1970s, Starobinsky worked on the theory of particle creation in the early universe and particle generation and radiation from rotating black holes (1973/74), a precursor of the theory of Hawking radiation. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Yakov Borisovich Zel'dovich
Yakov Borisovich Zeldovich ( be, Я́каў Бары́савіч Зяльдо́віч, russian: Я́ков Бори́сович Зельдо́вич; 8 March 1914 – 2 December 1987), also known as YaB, was a leading Soviet physicist of Belarusian origin, who is known for his prolific contributions in physical cosmology, physics of thermonuclear reactions, combustion, and hydrodynamical phenomena. From 1943, Zeldovich, a self-taught physicist, started his career by playing a crucial role in the development of the former Soviet program of nuclear weapons. In 1963, he returned to academia to embark on pioneering contributions on the fundamental understanding of the thermodynamics of black holes and expanding the scope of physical cosmology. Biography Early life and education Yakov Zeldovich was born into a Belarusian Jewish family in his grandfather's house in Minsk. However, in mid-1914, the Zeldovich family moved to Saint Petersburg. They resided there until August 1941 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cosmological Model
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of fundamental questions about its origin, structure, evolution, and ultimate fate.For an overview, see Cosmology as a science originated with the Copernican principle, which implies that celestial bodies obey identical physical laws to those on Earth, and Newtonian mechanics, which first allowed those physical laws to be understood. Physical cosmology, as it is now understood, began with the development in 1915 of Albert Einstein's general theory of relativity, followed by major observational discoveries in the 1920s: first, Edwin Hubble discovered that the universe contains a huge number of external galaxies beyond the Milky Way; then, work by Vesto Slipher and others showed that the universe is expanding. These advances made it possible ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |