|
228 (number)
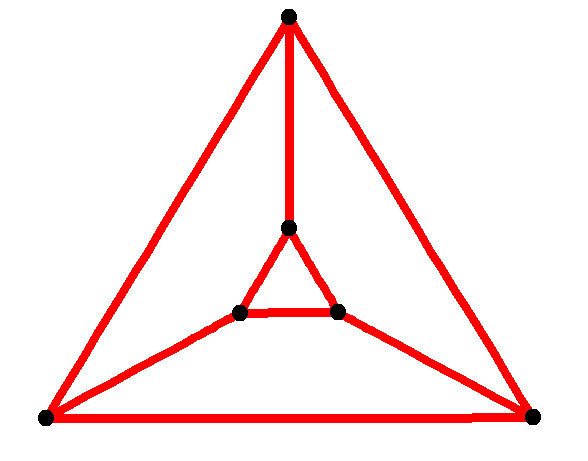
228 (two hundred ndtwenty-eight) is the natural number following 227 and preceding 229. In mathematics 228 is a refactorable number and a practical number. There are 228 matchings in a ladder graph with five rungs. 228 is the smallest even number ''n'' such that the numerator of the ''n''th Bernoulli number is divisible by a nontrivial square number that is relatively prime In mathematics, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equival ... to ''n''. The binary form of 228 contains all the two digit binary numbers in sequence from highest to lowest (11 10 01 00). References Integers {{Num-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called '' cardinal numbers'', and numbers used for ordering are called '' ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports jersey numbers). Some definitions, including the standard ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural numbers form a set. Many other number sets are built by succ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
227 (number)
227 (two hundred ndtwenty-seven) is the natural number between 226 and 228. It is also a prime number. In mathematics 227 is a twin prime and the start of a prime triplet (with 229 and 233). It is a safe prime, as dividing it by two and rounding down produces the Sophie Germain prime 113. It is also a regular prime, a Pillai prime, a Stern prime, and a Ramanujan prime. 227 and 229 form the first twin prime pair for which neither is a cluster prime. The 227th harmonic number is the first to exceed six. There are 227 different connected graphs with eight edges, and 227 independent sets in a 3 × 4 grid graph In graph theory, a lattice graph, mesh graph, or grid graph is a graph whose drawing, embedded in some Euclidean space , forms a regular tiling. This implies that the group of bijective transformations that send the graph to itself is a lat .... References Integers {{Num-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
229 (number)
229 (two hundred ndtwenty-nine) is the natural number following 228 and preceding 230. In mathematics It is a prime number, and a regular prime. It is also a full reptend prime, meaning that the decimal expansion of the unit fraction 1/229 repeats periodically with as long a period as possible. With 227 it is the larger of a pair of twin primes, and it is also the start of a sequence of three consecutive squarefree numbers. It is the smallest prime that, when added to the reverse of its decimal representation, yields another prime: 229 + 922 = 1151. There are 229 cyclic permutations of the numbers from 1 to 7 in which none of the numbers is mapped to its successor (mod 7), 229 rooted tree structures formed from nine carbon atoms, and 229 triangulations of a polygon formed by adding three vertices to each side of a triangle. There are also 229 different projective configurations of type (123123), in which twelve points and twelve lines meet with three lines ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Refactorable Number
A refactorable number or tau number is an integer ''n'' that is divisible by the count of its divisors, or to put it algebraically, ''n'' is such that \tau(n)\mid n. The first few refactorable numbers are listed in as : 1, 2, 8, 9, 12, 18, 24, 36, 40, 56, 60, 72, 80, 84, 88, 96, 104, 108, 128, 132, 136, 152, 156, 180, 184, 204, 225, 228, 232, 240, 248, 252, 276, 288, 296, ... For example, 18 has 6 divisors (1 and 18, 2 and 9, 3 and 6) and is divisible by 6. There are infinitely many refactorable numbers. Properties Cooper and Kennedy proved that refactorable numbers have natural density zero. Zelinsky proved that no three consecutive integers can all be refactorable. Colton proved that no refactorable number is perfect. The equation \gcd(n,x) = \tau(n) has solutions only if n is a refactorable number, where \gcd is the greatest common divisor function. Let T(x) be the number of refactorable numbers which are at most x. The problem of determining an asymptot ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Practical Number
In number theory, a practical number or panarithmic number is a positive integer n such that all smaller positive integers can be represented as sums of distinct divisors of n. For example, 12 is a practical number because all the numbers from 1 to 11 can be expressed as sums of its divisors 1, 2, 3, 4, and 6: as well as these divisors themselves, we have 5 = 3 + 2, 7 = 6 + 1, 8 = 6 + 2, 9 = 6 + 3, 10 = 6 + 3 + 1, and 11 = 6 + 3 + 2. The sequence of practical numbers begins Practical numbers were used by Fibonacci in his Liber Abaci (1202) in connection with the problem of representing rational numbers as Egyptian fractions. Fibonacci does not formally define practical numbers, but he gives a table of Egyptian fraction expansions for fractions with practical denominators.. The name "practical number" is due to . He noted that "the subdivisions of money, weights, and measures involve numbers like 4, 12, 16, 20 and 28 which are usually supposed to be so inconvenient as to dese ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matching (graph Theory)
In the mathematical discipline of graph theory, a matching or independent edge set in an undirected graph is a set of edges without common vertices. Finding a matching in a bipartite graph can be treated as a network flow problem. Definitions Given a graph a matching ''M'' in ''G'' is a set of pairwise non-adjacent edges, none of which are loops; that is, no two edges share common vertices. A vertex is matched (or saturated) if it is an endpoint of one of the edges in the matching. Otherwise the vertex is unmatched (or unsaturated). A maximal matching is a matching ''M'' of a graph ''G'' that is not a subset of any other matching. A matching ''M'' of a graph ''G'' is maximal if every edge in ''G'' has a non-empty intersection with at least one edge in ''M''. The following figure shows examples of maximal matchings (red) in three graphs. : A maximum matching (also known as maximum-cardinality matching) is a matching that contains the largest possible number of edges. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ladder Graph
In the mathematical field of graph theory, the ladder graph is a planar, undirected graph with vertices and edges. The ladder graph can be obtained as the Cartesian product of two path graphs, one of which has only one edge: . Properties By construction, the ladder graph L''n'' is isomorphic to the grid graph ''G''2,''n'' and looks like a ladder with ''n'' rungs. It is Hamiltonian with girth 4 (if ''n>1'') and chromatic index 3 (if ''n>2''). The chromatic number of the ladder graph is 2 and its chromatic polynomial is (x-1)x(x^2-3x+3)^. Image:Ladder graph L8 2COL.svg, The chromatic number of the ladder graph is 2. Ladder rung graph Sometimes the term "ladder graph" is used for the ''n'' × ''P''2 ladder rung graph, which is the graph union of ''n'' copies of the path graph P2. Circular ladder graph The circular ladder graph ''CL''''n'' is constructible by connecting the four 2-degree vertices in a ''straight'' way, or by the Cartesian product of a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bernoulli Number
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, in Faulhaber's formula for the sum of ''m''-th powers of the first ''n'' positive integers, in the Euler–Maclaurin formula, and in expressions for certain values of the Riemann zeta function. The values of the first 20 Bernoulli numbers are given in the adjacent table. Two conventions are used in the literature, denoted here by B^_n and B^_n; they differ only for , where B^_1=-1/2 and B^_1=+1/2. For every odd , . For every even , is negative if is divisible by 4 and positive otherwise. The Bernoulli numbers are special values of the Bernoulli polynomials B_n(x), with B^_n=B_n(0) and B^+_n=B_n(1). The Bernoulli numbers were discovered around the same time by the Swiss mathematician Jacob Bernoulli, after whom they are named, and i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of figurate numbers (other examples being cube numbers and triangular numbers). Square numbers are non-negative. A non-negative integer is a square number when its square root is again an integer. For example, \sqrt = 3, so 9 is a squ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Relatively Prime
In mathematics, two integers and are coprime, relatively prime or mutually prime if the only positive integer that is a divisor of both of them is 1. Consequently, any prime number that divides does not divide , and vice versa. This is equivalent to their greatest common divisor (GCD) being 1. One says also '' is prime to '' or '' is coprime with ''. The numbers 8 and 9 are coprime, despite the fact that neither considered individually is a prime number, since 1 is their only common divisor. On the other hand, 6 and 9 are not coprime, because they are both divisible by 3. The numerator and denominator of a reduced fraction are coprime, by definition. Notation and testing Standard notations for relatively prime integers and are: and . In their 1989 textbook '' Concrete Mathematics'', Ronald Graham, Donald Knuth, and Oren Patashnik proposed that the notation a\perp b be used to indicate that and are relatively prime and that the term "prime" be used instead of coprime ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |