|
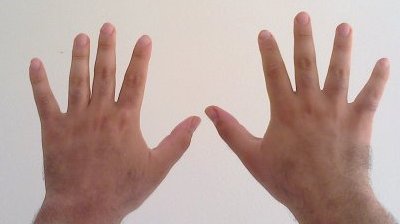
26 (number)
26 (twenty-six) is the natural number following 25 and preceding 27. In mathematics *26 is the only integer that is one greater than a square (5 + 1) and one less than a cube (3 − 1). *26 is a telephone number, specifically, the number of ways of connecting 5 points with pairwise connections. *There are 26 sporadic groups. *The 26-dimensional Lorentzian unimodular lattice II25,1 plays a significant role in sphere packing problems and the classification of finite simple groups. In particular, the Leech lattice is obtained in a simple way as a subquotient. *26 is the smallest number that is both a nontotient and a noncototient number. *There are 26 faces of a rhombicuboctahedron. *When a 3 × 3 × 3 cube is made of 27 unit cubes, 26 of them are viewable as the exterior layer. Also a 26 sided polygon is called an icosihexagon. *φ(26) = φ(σ(26)). Properties of its positional representation in certain radixes Twenty-six is a repdigit in base three (2223) and in base 12 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Natural Number
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country"). Numbers used for counting are called ''Cardinal number, cardinal numbers'', and numbers used for ordering are called ''Ordinal number, ordinal numbers''. Natural numbers are sometimes used as labels, known as ''nominal numbers'', having none of the properties of numbers in a mathematical sense (e.g. sports Number (sports), jersey numbers). Some definitions, including the standard ISO/IEC 80000, ISO 80000-2, begin the natural numbers with , corresponding to the non-negative integers , whereas others start with , corresponding to the positive integers Texts that exclude zero from the natural numbers sometimes refer to the natural numbers together with zero as the whole numbers, while in other writings, that term is used instead for the integers (including negative integers). The natural ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
List Of Polygons
In geometry, a polygon is traditionally a plane figure that is bounded by a finite chain of straight line segments closing in a loop to form a closed chain. These segments are called its ''edges'' or ''sides'', and the points where two of the edges meet are the polygon's '' vertices'' (singular: vertex) or ''corners''. The word ''polygon'' comes from Late Latin ''polygōnum'' (a noun), from Greek πολύγωνον (''polygōnon/polugōnon''), noun use of neuter of πολύγωνος (''polygōnos/polugōnos'', the masculine adjective), meaning "many-angled". Individual polygons are named (and sometimes classified) according to the number of sides, combining a Greek-derived numerical prefix with the suffix ''-gon'', e.g. '' pentagon'', ''dodecagon''. The triangle, quadrilateral and nonagon are exceptions, although the regular forms ''trigon'', ''tetragon'', and ''enneagon'' are sometimes encountered as well. Greek numbers Polygons are primarily named by prefixes from Ancient ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Messier Object
The Messier objects are a set of 110 astronomical objects catalogued by the French astronomer Charles Messier in his ''Catalogue des Nébuleuses et des Amas d'Étoiles'' (''Catalogue of Nebulae and Star Clusters''). Because Messier was only interested in finding comets, he created a list of those non-comet objects that frustrated his hunt for them. The compilation of this list, in collaboration with his assistant Pierre Méchain, is known as ''the Messier catalogue''. This catalogue of objects is one of the most famous lists of astronomical objects, and many Messier objects are still referenced by their Messier numbers. The catalogue includes most of the astronomical deep-sky objects that can easily be observed from Earth's Northern Hemisphere; many Messier objects are popular targets for amateur astronomers. A preliminary version first appeared in 1774 in the ''Memoirs'' of the French Academy of Sciences for the year 1771. The first version of Messier's catalogue contain ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bosonic String Theory
Bosonic string theory is the original version of string theory, developed in the late 1960s and named after Satyendra Nath Bose. It is so called because it contains only bosons in the spectrum. In the 1980s, supersymmetry was discovered in the context of string theory, and a new version of string theory called superstring theory (supersymmetric string theory) became the real focus. Nevertheless, bosonic string theory remains a very useful model to understand many general features of perturbative string theory, and many theoretical difficulties of superstrings can actually already be found in the context of bosonic strings. Problems Although bosonic string theory has many attractive features, it falls short as a viable physical model in two significant areas. First, it predicts only the existence of bosons whereas many physical particles are fermions. Second, it predicts the existence of a mode of the string with imaginary mass, implying that the theory has an instability t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dimension
In physics and mathematics, the dimension of a Space (mathematics), mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any Point (geometry), point within it. Thus, a Line (geometry), line has a dimension of one (1D) because only one coordinate is needed to specify a point on itfor example, the point at 5 on a number line. A Surface (mathematics), surface, such as the Boundary (mathematics), boundary of a Cylinder (geometry), cylinder or sphere, has a dimension of two (2D) because two coordinates are needed to specify a point on itfor example, both a latitude and longitude are required to locate a point on the surface of a sphere. A two-dimensional Euclidean space is a two-dimensional space on the Euclidean plane, plane. The inside of a cube, a cylinder or a sphere is three-dimensional (3D) because three coordinates are needed to locate a point within these spaces. In classical mechanics, space and time are different categ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spacetime
In physics, spacetime is a mathematical model that combines the three dimensions of space and one dimension of time into a single four-dimensional manifold. Spacetime diagrams can be used to visualize relativistic effects, such as why different observers perceive differently where and when events occur. Until the 20th century, it was assumed that the three-dimensional geometry of the universe (its spatial expression in terms of coordinates, distances, and directions) was independent of one-dimensional time. The physicist Albert Einstein helped develop the idea of spacetime as part of his theory of relativity. Prior to his pioneering work, scientists had two separate theories to explain physical phenomena: Isaac Newton's laws of physics described the motion of massive objects, while James Clerk Maxwell's electromagnetic models explained the properties of light. However, in 1905, Einstein based a work on special relativity on two postulates: * The laws of physics are invariant ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Iron
Iron () is a chemical element with symbol Fe (from la, ferrum) and atomic number 26. It is a metal that belongs to the first transition series and group 8 of the periodic table. It is, by mass, the most common element on Earth, right in front of oxygen (32.1% and 30.1%, respectively), forming much of Earth's outer and inner core. It is the fourth most common element in the Earth's crust. In its metallic state, iron is rare in the Earth's crust, limited mainly to deposition by meteorites. Iron ores, by contrast, are among the most abundant in the Earth's crust, although extracting usable metal from them requires kilns or furnaces capable of reaching or higher, about higher than that required to smelt copper. Humans started to master that process in Eurasia during the 2nd millennium BCE and the use of iron tools and weapons began to displace copper alloys, in some regions, only around 1200 BCE. That event is considered the transition from the Bronze Age to the Iron A ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Atomic Number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of an atomic nucleus. For ordinary nuclei, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every atom of that element. The atomic number can be used to uniquely identify ordinary chemical elements. In an ordinary uncharged atom, the atomic number is also equal to the number of electrons. For an ordinary atom, the sum of the atomic number ''Z'' and the neutron number ''N'' gives the atom's atomic mass number ''A''. Since protons and neutrons have approximately the same mass (and the mass of the electrons is negligible for many purposes) and the mass defect of the nucleon binding is always small compared to the nucleon mass, the atomic mass of any atom, when expressed in unified atomic mass units (making a quantity called the "relative isotopic mass"), is within 1% of the whole number ''A''. Atoms with the same atomic number but dif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
676 (number)
600 (six hundred) is the natural number following 599 and preceding 601. Mathematical properties Six hundred is a composite number, an abundant number, a pronic number and a Harshad number. Credit and cars * In the United States, a credit score of 600 or below is considered poor, limiting available credit at a normal interest rate. * NASCAR runs 600 advertised miles in the Coca-Cola 600, its longest race. * The Fiat 600 is a car, the SEAT 600 its Spanish version. Integers from 601 to 699 600s * 601 = prime number, centered pentagonal number * 602 = 2 × 7 × 43, nontotient, number of cubes of edge length 1 required to make a hollow cube of edge length 11, area code for Phoenix, AZ along with 480 and 623 * 603 = 32 × 67, Harshad number, Riordan number, area code for New Hampshire * 604 = 22 × 151, nontotient, totient sum for first 44 integers, area code for southwestern British Columbia (Lower Mainland, Fraser Valley, Sunshine Coast and Sea to Sky) * 605 = 5 × 112, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square Number
In mathematics, a square number or perfect square is an integer that is the square (algebra), square of an integer; in other words, it is the multiplication, product of some integer with itself. For example, 9 is a square number, since it equals and can be written as . The usual notation for the square of a number is not the product , but the equivalent exponentiation , usually pronounced as " squared". The name ''square'' number comes from the name of the shape. The unit of area is defined as the area of a unit square (). Hence, a square with side length has area . If a square number is represented by ''n'' points, the points can be arranged in rows as a square each side of which has the same number of points as the square root of ''n''; thus, square numbers are a type of figurate numbers (other examples being Cube (algebra), cube numbers and triangular numbers). Square numbers are non-negative. A non-negative integer is a square number when its square root is again an intege ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Palindrome
A palindrome is a word, number, phrase, or other sequence of symbols that reads the same backwards as forwards, such as the words ''madam'' or ''racecar'', the date and time ''11/11/11 11:11,'' and the sentence: "A man, a plan, a canal – Panama". The 19-letter Finnish word ''saippuakivikauppias'' (a soapstone vendor), is the longest single-word palindrome in everyday use, while the 12-letter term ''tattarrattat'' (from James Joyce in ''Ulysses'') is the longest in English. The word ''palindrome'' was introduced by English poet and writer Henry Peacham in 1638.Henry Peacham, ''The Truth of our Times Revealed out of One Mans Experience'', 1638p. 123/ref> The concept of a palindrome can be dated to the 3rd-century BCE, although no examples survive; the first physical examples can be dated to the 1st-century CE with the Latin acrostic word square, the Sator Square (contains both word and sentence palindromes), and the 4th-century Greek Byzantine sentence palindrome ''nipson ano ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral system. The way of denoting numbers in the decimal system is often referred to as ''decimal notation''. A ''decimal numeral'' (also often just ''decimal'' or, less correctly, ''decimal number''), refers generally to the notation of a number in the decimal numeral system. Decimals may sometimes be identified by a decimal separator (usually "." or "," as in or ). ''Decimal'' may also refer specifically to the digits after the decimal separator, such as in " is the approximation of to ''two decimals''". Zero-digits after a decimal separator serve the purpose of signifying the precision of a value. The numbers that may be represented in the decimal system are the decimal fractions. That is, fractions of the form , where is an integer, and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |