|
2-factor
In graph theory, a factor of a graph ''G'' is a spanning subgraph, i.e., a subgraph that has the same vertex set as ''G''. A ''k''-factor of a graph is a spanning ''k''-regular subgraph, and a ''k''-factorization partitions the edges of the graph into disjoint ''k''-factors. A graph ''G'' is said to be ''k''-factorable if it admits a ''k''-factorization. In particular, a 1-factor is a perfect matching, and a 1-factorization of a ''k''-regular graph is a proper edge coloring with ''k'' colors. A 2-factor is a collection of disjoint cycles that spans all vertices of the graph. 1-factorization If a graph is 1-factorable then it has to be a regular graph. However, not all regular graphs are 1-factorable. A ''k''-regular graph is 1-factorable if it has chromatic index ''k''; examples of such graphs include: * Any regular bipartite graph. Hall's marriage theorem can be used to show that a ''k''-regular bipartite graph contains a perfect matching. One can then remove the perfect ma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Julius Petersen
Julius Peter Christian Petersen (16 June 1839 in Sorø, West Zealand – 5 August 1910 in Copenhagen) was a Denmark, Danish mathematician. His contributions to the field of mathematics led to the birth of graph theory. Biography Petersen's interests in mathematics were manifold, including: geometry, complex analysis, number theory, mathematical physics, mathematical economics, cryptography and graph theory. His famous paper ''Die Theorie der regulären graphs'' was a fundamental contribution to modern graph theory as we know it today. In 1898, he presented a counterexample to Peter Guthrie Tait, Tait's claimed theorem about 1-factorability of 3-regular graphs, which is nowadays known as the "Petersen graph". In cryptography and mathematical economics he made contributions which today are seen as pioneering. He published a systematic treatment of geometry, geometrical constructions (with straightedge and compass) in 1880. A French language, French translation was reprinted in 1 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Petersen Graph
In the mathematical field of graph theory, the Petersen graph is an undirected graph with 10 vertices and 15 edges. It is a small graph that serves as a useful example and counterexample for many problems in graph theory. The Petersen graph is named after Julius Petersen, who in 1898 constructed it to be the smallest bridgeless cubic graph with no three- edge-coloring. Although the graph is generally credited to Petersen, it had in fact first appeared 12 years earlier, in a paper by . Kempe observed that its vertices can represent the ten lines of the Desargues configuration, and its edges represent pairs of lines that do not meet at one of the ten points of the configuration. Donald Knuth states that the Petersen graph is "a remarkable configuration that serves as a counterexample to many optimistic predictions about what might be true for graphs in general." The Petersen graph also makes an appearance in tropical geometry. The cone over the Petersen graph is naturally ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graph Theory
In mathematics and computer science, graph theory is the study of ''graph (discrete mathematics), graphs'', which are mathematical structures used to model pairwise relations between objects. A graph in this context is made up of ''Vertex (graph theory), vertices'' (also called ''nodes'' or ''points'') which are connected by ''Glossary of graph theory terms#edge, edges'' (also called ''arcs'', ''links'' or ''lines''). A distinction is made between undirected graphs, where edges link two vertices symmetrically, and directed graphs, where edges link two vertices asymmetrically. Graphs are one of the principal objects of study in discrete mathematics. Definitions Definitions in graph theory vary. The following are some of the more basic ways of defining graphs and related mathematical structures. Graph In one restricted but very common sense of the term, a graph is an ordered pair G=(V,E) comprising: * V, a Set (mathematics), set of vertices (also called nodes or points); * ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
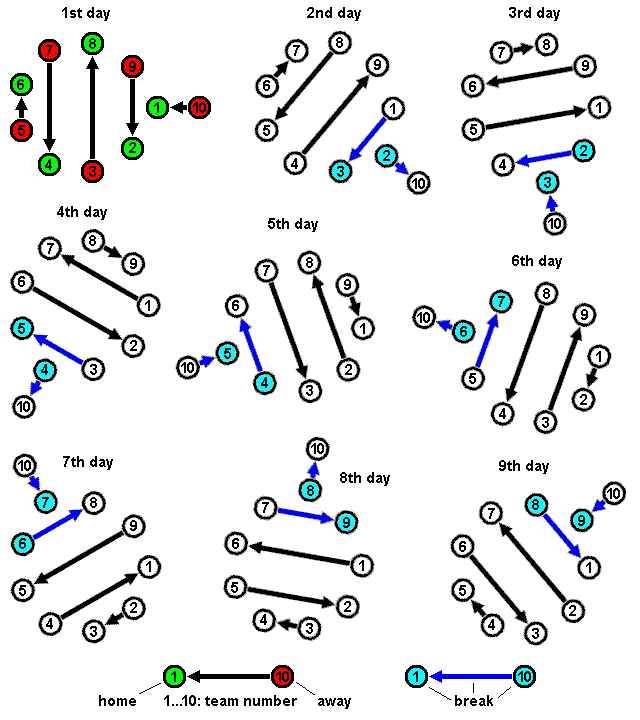
Round-robin Tournament
A round-robin tournament or all-play-all tournament is a competition format in which each contestant meets every other participant, usually in turn.''Webster's Third New International Dictionary of the English Language, Unabridged'' (1971, G. & C. Merriam Co), p.1980. A round-robin contrasts with an elimination tournament, wherein participants are eliminated after a certain number of wins or losses. Terminology The term ''round-robin'' is derived from the French term ('ribbon'). Over time, the term became idiomized to ''robin''. In a ''single round-robin'' schedule, each participant plays every other participant once. If each participant plays all others twice, this is frequently called a ''double round-robin''. The term is rarely used when all participants play one another more than twice, and is never used when one participant plays others an unequal number of times, as is the case in almost all of the major North American professional sports leagues. In the United Kingdom, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Complete Bipartite Graph
In the mathematical field of graph theory, a complete bipartite graph or biclique is a special kind of bipartite graph where every vertex of the first set is connected to every vertex of the second set..Electronic edition page 17. Graph theory itself is typically dated as beginning with Leonhard Euler's 1736 work on the Seven Bridges of Königsberg. However, drawings of complete bipartite graphs were already printed as early as 1669, in connection with an edition of the works of Ramon Llull edited by Athanasius Kircher. Llull himself had made similar drawings of complete graphs three centuries earlier.. Definition A complete bipartite graph is a graph whose vertices can be partitioned into two subsets and such that no edge has both endpoints in the same subset, and every possible edge that could connect vertices in different subsets is part of the graph. That is, it is a bipartite graph such that for every two vertices and, is an edge in . A complete bipartite graph w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prime Number
A prime number (or a prime) is a natural number greater than 1 that is not a Product (mathematics), product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways of writing it as a product, or , involve 5 itself. However, 4 is composite because it is a product (2 × 2) in which both numbers are smaller than 4. Primes are central in number theory because of the fundamental theorem of arithmetic: every natural number greater than 1 is either a prime itself or can be factorization, factorized as a product of primes that is unique up to their order. The property of being prime is called primality. A simple but slow primality test, method of checking the primality of a given number , called trial division, tests whether is a multiple of any integer between 2 and . Faster algorithms include the Miller–Rabin primality test, which is fast but has a small chance of error ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Springer US
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing. Originally founded in 1842 in Berlin, it expanded internationally in the 1960s, and through mergers in the 1990s and a sale to venture capitalists it fused with Wolters Kluwer and eventually became part of Springer Nature in 2015. Springer has major offices in Berlin, Heidelberg, Dordrecht, and New York City. History Julius Springer founded Springer-Verlag in Berlin in 1842 and his son Ferdinand Springer grew it from a small firm of 4 employees into Germany's then second-largest academic publisher with 65 staff in 1872.Chronology ". Springer Science+Business Media. In 1964, Springer expanded its business internationally, op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Anton Kotzig
Anton Kotzig (22 October 1919 – 20 April 1991) was a Slovak–Canadian mathematician, expert in statistics, combinatorics and graph theory. A number of his mathematical contributions are named after him. These include the Ringel–Kotzig conjecture on graceful labeling of trees (with Gerhard Ringel); Kotzig's conjecture on regularly path connected graphs; Kotzig's theorem on the degrees of vertices in convex polyhedra; as well as the Kotzig transformation. Biography Kotzig was born in Kočovce, a village in Western Slovakia. He studied at the secondary grammar school in Nové Mesto nad Váhom, and began his undergraduate studies at the Charles University in Prague. After the closure of Czech universities in 1939, he moved to Bratislava where in 1943, he earned a doctoral degree (RNDr.) in Mathematical Statistics from the Comenius University. He remained in Bratislava working at the Central Bureau of Social Insurance for Slovakia as head of the Department of Mathemat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hamiltonian Cycle
In the mathematics, mathematical field of graph theory, a Hamiltonian path (or traceable path) is a path (graph theory), path in an undirected or directed graph that visits each vertex (graph theory), vertex exactly once. A Hamiltonian cycle (or Hamiltonian circuit) is a cycle (graph theory), cycle that visits each vertex exactly once. A Hamiltonian path that starts and ends at adjacent vertices can be completed by adding one more edge to form a Hamiltonian cycle, and removing any edge from a Hamiltonian cycle produces a Hamiltonian path. The computational problems of determining whether such paths and cycles exist in graphs are NP-complete; see Hamiltonian path problem for details. Hamiltonian paths and cycles are named after William Rowan Hamilton, who invented the icosian game, now also known as ''Hamilton's puzzle'', which involves finding a Hamiltonian cycle in the edge graph of the dodecahedron. Hamilton solved this problem using the icosian calculus, an algebraic structur ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Glossary Of Graph Theory
This is a glossary of graph theory. Graph theory is the study of graphs, systems of nodes or vertices connected in pairs by lines or edges. Symbols A B C D E F G H I J K L M ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Overfull Conjecture
In graph theory, an overfull graph is a graph whose size is greater than the product of its maximum degree and half of its order floored, i.e. , E, > \Delta (G) \lfloor , V, /2 \rfloor where , E, is the size of ''G'', \displaystyle\Delta(G) is the maximum degree of ''G'', and , V, is the order of ''G''. The concept of an overfull subgraph, an overfull graph that is a subgraph, immediately follows. An alternate, stricter definition of an overfull subgraph ''S'' of a graph ''G'' requires \displaystyle\Delta (G) = \Delta (S). Examples Every odd cycle graph of length three or more is overfull. The product of its degree (two) and half its length (rounded down) is one less than the number of edges in the cycle. More generally, every regular graph with an odd number n of vertices is overfull, because its number of edges, \Delta n/2 (where \Delta is its degree), is larger than \Delta\lfloor n/2\rfloor. Properties A few properties of overfull graphs: # Overfull graphs are of odd orde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), have shaped much of mathematical history as new areas of mathematics are developed in order to prove them. Resolution of conjectures Proof Formal mathematics is based on ''provable'' truth. In mathematics, any number of cases supporting a universally quantified conjecture, no matter how large, is insufficient for establishing the conjecture's veracity, since a single counterexample could immediately bring down the conjecture. Mathematical journals sometimes publish the minor results of research teams having extended the search for a counterexample farther than previously done. For instance, the Collatz conjecture, which concerns whether or not certain sequences of integers terminate, has been tested for all integers up to 1.2 × 101 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |