Wiedemann–Franz law on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Qualitatively, this relationship is based upon the fact that the heat and electrical transport both involve the free electrons in the metal.
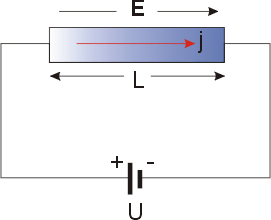
The mathematical expression of the law can be derived as following. Electrical conduction of metals is a well-known phenomenon and is attributed to the free conduction electrons, which can be measured as sketched in the figure. The
Qualitatively, this relationship is based upon the fact that the heat and electrical transport both involve the free electrons in the metal.
The mathematical expression of the law can be derived as following. Electrical conduction of metals is a well-known phenomenon and is attributed to the free conduction electrons, which can be measured as sketched in the figure. The

physics
Physics is the scientific study of matter, its Elementary particle, fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge whi ...
, the Wiedemann–Franz law states that the ratio of the electronic contribution of the thermal conductivity
The thermal conductivity of a material is a measure of its ability to heat conduction, conduct heat. It is commonly denoted by k, \lambda, or \kappa and is measured in W·m−1·K−1.
Heat transfer occurs at a lower rate in materials of low ...
(''κ'') to the electrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
(''σ'') of a metal
A metal () is a material that, when polished or fractured, shows a lustrous appearance, and conducts electrical resistivity and conductivity, electricity and thermal conductivity, heat relatively well. These properties are all associated wit ...
is proportional to the temperature
Temperature is a physical quantity that quantitatively expresses the attribute of hotness or coldness. Temperature is measurement, measured with a thermometer. It reflects the average kinetic energy of the vibrating and colliding atoms making ...
(''T'').
:
Theoretically, the proportionality constant ''L'', known as the Lorenz number, is equal to
:
where ''k''B is the Boltzmann constant
The Boltzmann constant ( or ) is the proportionality factor that relates the average relative thermal energy of particles in a ideal gas, gas with the thermodynamic temperature of the gas. It occurs in the definitions of the kelvin (K) and the ...
and ''e'' is the elementary charge
The elementary charge, usually denoted by , is a fundamental physical constant, defined as the electric charge carried by a single proton (+1 ''e'') or, equivalently, the magnitude of the negative electric charge carried by a single electron, ...
.
This empirical
Empirical evidence is evidence obtained through sense experience or experimental procedure. It is of central importance to the sciences and plays a role in various other fields, like epistemology and law.
There is no general agreement on how t ...
law is named after Gustav Wiedemann and Rudolph Franz, who in 1853 reported that ''κ''/''σ'' has approximately the same value for different metals at the same temperature. The proportionality of ''κ''/''σ'' with temperature was discovered by Ludvig Lorenz
Ludvig Valentin Lorenz ( ; 18 January 1829 – 9 June 1891) was a Danish physicist and mathematician. In 1867, he gave completely general integral solutions to the differential equations of electromagnetism, which contain retardation effects re ...
in 1872.
Derivation
 Qualitatively, this relationship is based upon the fact that the heat and electrical transport both involve the free electrons in the metal.
The mathematical expression of the law can be derived as following. Electrical conduction of metals is a well-known phenomenon and is attributed to the free conduction electrons, which can be measured as sketched in the figure. The
Qualitatively, this relationship is based upon the fact that the heat and electrical transport both involve the free electrons in the metal.
The mathematical expression of the law can be derived as following. Electrical conduction of metals is a well-known phenomenon and is attributed to the free conduction electrons, which can be measured as sketched in the figure. The current density
In electromagnetism, current density is the amount of charge per unit time that flows through a unit area of a chosen cross section. The current density vector is defined as a vector whose magnitude is the electric current per cross-sectional ...
''j'' is observed to be proportional to the applied electric field
An electric field (sometimes called E-field) is a field (physics), physical field that surrounds electrically charged particles such as electrons. In classical electromagnetism, the electric field of a single charge (or group of charges) descri ...
and follows Ohm's law
Ohm's law states that the electric current through a Electrical conductor, conductor between two Node (circuits), points is directly Proportionality (mathematics), proportional to the voltage across the two points. Introducing the constant of ...
where the prefactor is the specific electrical conductivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity in ...
. Since the electric field and the current density are vector
Vector most often refers to:
* Euclidean vector, a quantity with a magnitude and a direction
* Disease vector, an agent that carries and transmits an infectious pathogen into another living organism
Vector may also refer to:
Mathematics a ...
s Ohm's law is expressed here in bold face. The conductivity can in general be expressed as a tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects associated with a vector space. Tensors may map between different objects such as vectors, scalars, and even other ...
of the second rank (3×3 matrix
Matrix (: matrices or matrixes) or MATRIX may refer to:
Science and mathematics
* Matrix (mathematics), a rectangular array of numbers, symbols or expressions
* Matrix (logic), part of a formula in prenex normal form
* Matrix (biology), the m ...
). Here we restrict the discussion to isotropic
In physics and geometry, isotropy () is uniformity in all orientations. Precise definitions depend on the subject area. Exceptions, or inequalities, are frequently indicated by the prefix ' or ', hence '' anisotropy''. ''Anisotropy'' is also ...
, i.e. scalar conductivity. The specific resistivity
Electrical resistivity (also called volume resistivity or specific electrical resistance) is a fundamental specific property of a material that measures its electrical resistance or how strongly it resists electric current. A low resistivity i ...
is the inverse of the conductivity. Both parameters will be used in the following.
The thermal conductivity is given by where is the heat capacity per electron, is the number density of charge carriers, is the mean free path
In physics, mean free path is the average distance over which a moving particle (such as an atom, a molecule, or a photon) travels before substantially changing its direction or energy (or, in a specific context, other properties), typically as a ...
of the electrons, and is the mean speed of the carriers.
The electrical conductivity is given by
: .
where is the mean free time and ''m'' the mass of the charge carriers.
The ratio is given by Drude model derivation
Paul Drude (c. 1900) realized that the phenomenological description of conductivity can be formulated quite generally (electron-, ion-, heat- etc. conductivity). Although the phenomenological description is incorrect for conduction electrons, it can serve as a preliminary treatment. The assumption is that the electrons move freely in the solid like in anideal gas
An ideal gas is a theoretical gas composed of many randomly moving point particles that are not subject to interparticle interactions. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is ...
. The force applied to the electron by the electric field leads to an acceleration
In mechanics, acceleration is the Rate (mathematics), rate of change of the velocity of an object with respect to time. Acceleration is one of several components of kinematics, the study of motion. Accelerations are Euclidean vector, vector ...
according to
:
:
This would lead, however, to a constant acceleration and, ultimately, to an infinite velocity. The further assumption therefore is that the electrons bump into obstacles (like defects or phonons
A phonon is a collective excitation in a periodic, Elasticity (physics), elastic arrangement of atoms or molecules in condensed matter physics, condensed matter, specifically in solids and some liquids. In the context of optically trapped objects ...
) once in a while which limits their free flight. This establishes an average or drift velocity
Drift or Drifts may refer to:
Geography
* Drift or ford (crossing) of a river
* Drift (navigation), difference between heading and course of a vessel
* Drift, Kentucky, unincorporated community in the United States
* In Cornwall, England:
** D ...
''V''d. The drift velocity is related to the average scattering time as becomes evident from the following relations.
:
For the kinetic theory of gases
The kinetic theory of gases is a simple classical model of the thermodynamic behavior of gases. Its introduction allowed many principal concepts of thermodynamics to be established. It treats a gas as composed of numerous particles, too small ...
, and
:
Therefore,
: ,
which is the Wiedemann–Franz law with an erroneous proportionality constant .
In Drude's original paper he used instead of , and also accidentally used a factor of 2. This meant his result is which is very close to experimental values. This is in fact due to 3 mistakes that conspired to make his result more accurate than warranted: the factor of 2 mistake; the specific heat per electron is in fact about 100 times less than ; the mean squared velocity of an electron is in fact about 100 times larger.
Free electron model
After taking into account the quantum effects, as in thefree electron model
In solid-state physics, the free electron model is a quantum mechanical model for the behaviour of charge carriers in a metallic solid. It was developed in 1927, principally by Arnold Sommerfeld, who combined the classical Drude model with quan ...
, the heat capacity is given by
: ,
where is the Fermi energy
The Fermi energy is a concept in quantum mechanics usually referring to the energy difference between the highest and lowest occupied single-particle states in a quantum system of non-interacting fermions at absolute zero temperature.
In a Fermi ga ...
and is the Fermi speed.
The proportionality constant is then corrected to , which agrees with experimental values.
Temperature dependence
The value ''L''0 = results from the fact that at low temperatures ( K) the heat and charge currents are carried by the same quasi-particles: electrons or holes. At finite temperatures two mechanisms produce a deviation of the ratio from the theoretical Lorenz value ''L''0: (i) other thermal carriers such as phonons or magnons, (ii)Inelastic scattering
In chemistry, nuclear physics, and particle physics, inelastic scattering is a process in which the internal states of a particle or a system of particles change after a collision. Often, this means the kinetic energy of the incident particle is n ...
.
As the temperature tends to 0 K, inelastic scattering becomes weak and promotes large q scattering values (trajectory ''a'' in the figure). For each electron transported, a thermal excitation is also carried and the Lorenz number is reached ''L'' = ''L''0. Note that in a perfect metal, inelastic scattering would be completely absent in the limit K and the thermal conductivity would vanish .
At finite temperature small q scattering values are possible (trajectory b in the figure) and electrons can be transported without the transport of a thermal excitation ''L''(''T'') < ''L''0.
At higher temperatures, the contribution of phonons to thermal transport in a system becomes important. This can lead to ''L''(''T'') > ''L''0. Above the Debye temperature
In thermodynamics and solid-state physics, the Debye model is a method developed by Peter Debye in 1912 to estimate phonon contribution to the specific heat (heat capacity) in a solid. It treats the oscillation, vibrations of the Crystal struct ...
the phonon contribution to thermal transport is constant and the ratio ''L''(''T'') is again found constant.
Limitations of the theory
Experiments have shown that the value of ''L'', while roughly constant, is not exactly the same for all materials. Charles Kittel's ''Introduction to Solid State Physics'' gives some values of ''L'' ranging from ''L'' = 2.23×10−8V2K−2 for copper at 0 °C to ''L'' = 3.2×10−8V2K−2 for tungsten at 100 °C. Rosenberg notes that the Wiedemann–Franz law is generally valid for high temperatures and for low (i.e., a few Kelvins) temperatures, but may not hold at intermediate temperatures. In many high purity metals both the electrical and thermal conductivities rise as temperature is decreased. In certain materials (such assilver
Silver is a chemical element; it has Symbol (chemistry), symbol Ag () and atomic number 47. A soft, whitish-gray, lustrous transition metal, it exhibits the highest electrical conductivity, thermal conductivity, and reflectivity of any metal. ...
or aluminum
Aluminium (or aluminum in North American English) is a chemical element; it has chemical symbol, symbol Al and atomic number 13. It has a density lower than that of other common metals, about one-third that of steel. Aluminium has ...
) however, the value of ''L'' also may decrease with temperature. In the purest samples of silver and at very low temperatures, ''L'' can drop by as much as a factor of 10.
In degenerate semiconductors, the Lorenz number ''L'' has a strong dependency on certain system parameters: dimensionality, strength of interatomic interactions and Fermi level
The Fermi level of a solid-state body is the thermodynamic work required to add one electron to the body. It is a thermodynamic quantity usually denoted by ''μ'' or ''E''F
for brevity. The Fermi level does not include the work required to re ...
. This law is not valid or the value of the Lorenz
number can be reduced at least in the following cases: manipulating electronic density of states
In condensed matter physics, the density of states (DOS) of a system describes the number of allowed modes or quantum state, states per unit energy range. The density of states is defined as where N(E)\delta E is the number of states in the syste ...
, varying doping density and layer thickness in superlattices and materials with correlated carriers. In thermoelectric materials there are also corrections due to boundary conditions, specifically open circuit vs. closed circuit.
A. J. Minnich, M. S. Dresselhaus, Z. F. Ren and G. Chen. Bulk nanostructured thermoelectric materials: current research and future prospects, Energy & Environmental Science, 2009, 2, 466–479,
Paothep Pichanusakorn, Prabhakar Bandaru. Nanostructured thermoelectrics, Materials Science and Engineering: R: Reports, Volume 67, Issues 2–4, 29 January 2010, pages 19–63, , .
Violations
In 2011, N. Wakeham et al. found that the ratio of the thermal and electrical Hall conductivities in the metallic phase of quasi-one-dimensional lithium molybdenum purple bronze Li0.9Mo6O17 diverges with decreasing temperature, reaching a value five orders of magnitude larger than that found in conventional metals obeying the Wiedemann–Franz law. This due to spin-charge separation and it behaving as aLuttinger liquid
A Luttinger liquid, or Tomonaga–Luttinger liquid, is a theoretical model describing interacting electrons (or other fermions) in a one-dimensional conductor (e.g. quantum wires such as carbon nanotubes). Such a model is necessary as the commonl ...
.
A Berkeley-led study in 2016 by S. Lee ''et al.'' also found a large violation of the Wiedemann–Franz law near the insulator-metal transition in VO2 nanobeams. In the metallic phase, the electronic contribution to thermal conductivity was much smaller than what would be expected from the Wiedemann–Franz law. The results can be explained in terms of independent propagation of charge and heat in a strongly correlated system.
Molecular systems
In 2020, Galen Craven and Abraham Nitzan derived a Wiedemann–Franz law for molecular systems in which electronic conduction is dominated not by free electron motion as in metals, but instead byelectron transfer
Electron transfer (ET) occurs when an electron relocates from an atom, ion, or molecule, to another such chemical entity. ET describes the mechanism by which electrons are transferred in redox reactions.
Electrochemical processes are ET reactio ...
between molecular sites. The molecular Wiedemann–Franz law is given by
:
where
:
is the Lorenz number for molecules and is the reorganization energy for electron transfer.
See also
* Drude modelReferences
{{DEFAULTSORT:Wiedemann-Franz law Heat conduction Electrical resistance and conductance Eponymous laws of physics