Taylor–Green Vortex

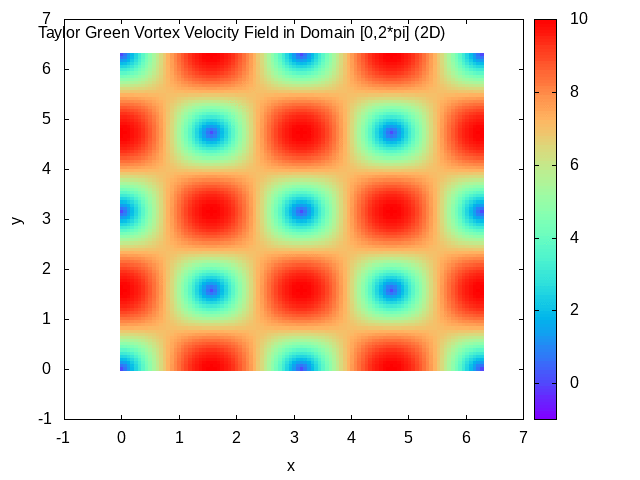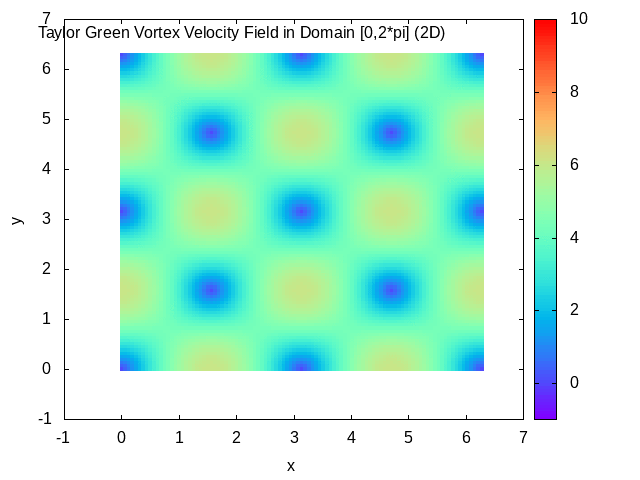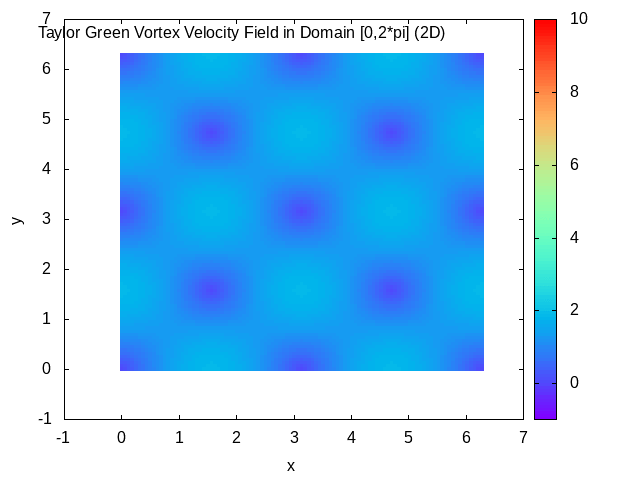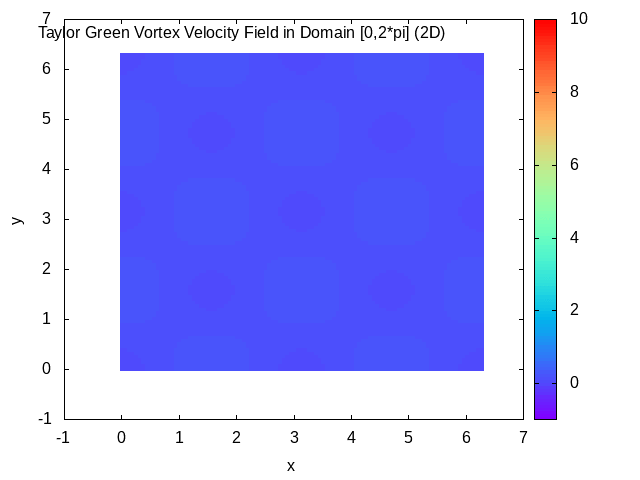In fluid dynamics, the Taylor–Green vortex is an unsteady flow of a decaying vortex, which has an exact closed form solution of the incompressible Navier–Stokes equations in Cartesian coordinates. It is named after the British physicist and mathematician Geoffrey Ingram Taylor and his collaborator A. E. Green.
Taylor, G. I. and Green, A. E., ''Mechanism of the Production of Small Eddies from Large Ones'', Proc. R. Soc. Lond. A, 158, 499–521 (1937).

Original work

In the original work of Taylor and Green, a particular flow is analyzed in three spatial dimensions, with the three velocity components $\mathbf=(u,v,w)$ at time $t=0$ specified by
:$u = A \cos ax \sin by \sin cz,$

:$v = B \sin ax \cos by \sin cz,$

:$w = C \sin ax \sin by \cos cz.$

The continuity equation $\nabla \cdot \mathbf=0$ determines that $Aa+Bb+Cc=0$. The small time behavior of the flow is then found through simplification of the incompressible Navier–Stokes equations using the initial flow to give a step-by-step solution as time progresses.

An exact solution in two spatial dimensions is known, and is presented below.

Incompressible Navier–Stokes equations

The incompressible Navier–Stokes equations in the absence of body force, and in two spatial dimensions, are given by
:$\frac+ \frac = 0,$

:$\frac + u\frac + v\frac = -\frac \frac + \nu \left( \frac + \frac \right),$

:$\frac + u\frac + v\frac = -\frac \frac + \nu \left( \frac + \frac \right).$
The first of the above equation represents the continuity equation and the other two represent the momentum equations.

Taylor–Green vortex solution

In the domain $0 \le x,y \le 2\pi$, the solution is given by

:$u = \cos x \sin y \,F(t), \qquad \qquad v = -\sin x \cos y \, F(t),$

where $F(t) = e^$, $\nu$ being the kinematic viscosity of the fluid. Following the analysis of Taylor and Green for the two-dimensional situation, and for $A=a=b=1$, gives agreement with this exact solution, if the exponential is expanded as a Taylor series, i.e. $F(t) = 1 - 2\nu t + O(t^2)$.

The pressure field $p$ can be obtained by substituting the velocity solution in the momentum equations and is given by

:$p = -\frac \left( \cos 2x + \cos 2y \right) F^2(t).$

The stream function of the Taylor–Green vortex solution, i.e. which satisfies $\mathbf = \nabla \times \boldsymbol$ for flow velocity $\mathbf$, is
:$\boldsymbol = -\cos x \cos y F(t)\, \hat.$

Similarly, the vorticity, which satisfies $\boldsymbol = \nabla \times \mathbf$, is given by
:$\boldsymbol = -2\cos x \cos y \,F(t) \hat.$

The Taylor–Green vortex solution may be used for testing and validation of temporal accuracy of Navier–Stokes algorithms.

A generalization of the Taylor–Green vortex solution in three dimensions in described in.

References

{{DEFAULTSORT:Taylor-Green vortex
Fluid dynamics
Computational fluid dynamics