Swarmalators on:
[Wikipedia]
[Google]
[Amazon]
Swarmalators are generalizations of phase oscillators that swarm around in space as they
 Biological microswimmers.
Biological microswimmers.
 The model above produces five collective states depicted in Figure 1:
* Static sync: Swarmalators form a disk in space and are fully synchronized in phase.
* Static async: Swarmalators form a disk in space and are fully asynchronous in phase.
* Static phase wave: Swarmalators form an annulus in space with a phase wave (e.g. a full color-wheel or rainbow.)
* Splintered phase wave: The phase wave splinters into clusters of synchronous swarmalators. Within each cluster, the swarmalators execute periodic motion in space and phase.
* Active phase wave: Swarmalators run in a space-phase vortex, with half running clockwise and the remaining half running counter-clockwise.
To demarcate where each state arises and disappears as a parameters are changed, the rainbow order parameters,
:
where are used. Figure 2 plots versus for fixed . As can be seen, in the rainbow-like static phased wave state (at = 0), and then declines as decreases. A second order parameter , defined as the fraction of swarmalators that have completed at least one cycle in space and phase after transients in also plotted, which can distinguish between the active phase wave and splintered phase wave states.
The model above produces five collective states depicted in Figure 1:
* Static sync: Swarmalators form a disk in space and are fully synchronized in phase.
* Static async: Swarmalators form a disk in space and are fully asynchronous in phase.
* Static phase wave: Swarmalators form an annulus in space with a phase wave (e.g. a full color-wheel or rainbow.)
* Splintered phase wave: The phase wave splinters into clusters of synchronous swarmalators. Within each cluster, the swarmalators execute periodic motion in space and phase.
* Active phase wave: Swarmalators run in a space-phase vortex, with half running clockwise and the remaining half running counter-clockwise.
To demarcate where each state arises and disappears as a parameters are changed, the rainbow order parameters,
:
where are used. Figure 2 plots versus for fixed . As can be seen, in the rainbow-like static phased wave state (at = 0), and then declines as decreases. A second order parameter , defined as the fraction of swarmalators that have completed at least one cycle in space and phase after transients in also plotted, which can distinguish between the active phase wave and splintered phase wave states.

 For unimodal distribution of such as the Cauchy distribution, the model exhibits four collective states depicted in the figure on the right.
* Async or state. Swarmalators do not exhibit any coherence either in space or phase, being distributed uniformly in position and phase. This state is characterized by the absence of any synchronization or spatial clustering among the swarmalators, as reflected by the zero values of both order parameters .
* Phase wave or state. In the phase wave state, swarmalators form a band or wave pattern with the position and phase are correlated. The wave can either run clockwise or counterclockwise.
* Mixed or state. Swaramlators again form a phase wave, but now the wave is distorted, forming two rough clusters; thus it is the a mixture of the phase wave and the sync state (described next).
* Sync or state. Swarmalators form two synchronous cluster in both space and phase. Single cluster states are formed for some initial conditions.
Note in each state, the swarmalators split into a locked/drifting sub-populations, just like the Kuramoto model. The locked population are the denser regions in the Figure, the drifters the light grey regions.
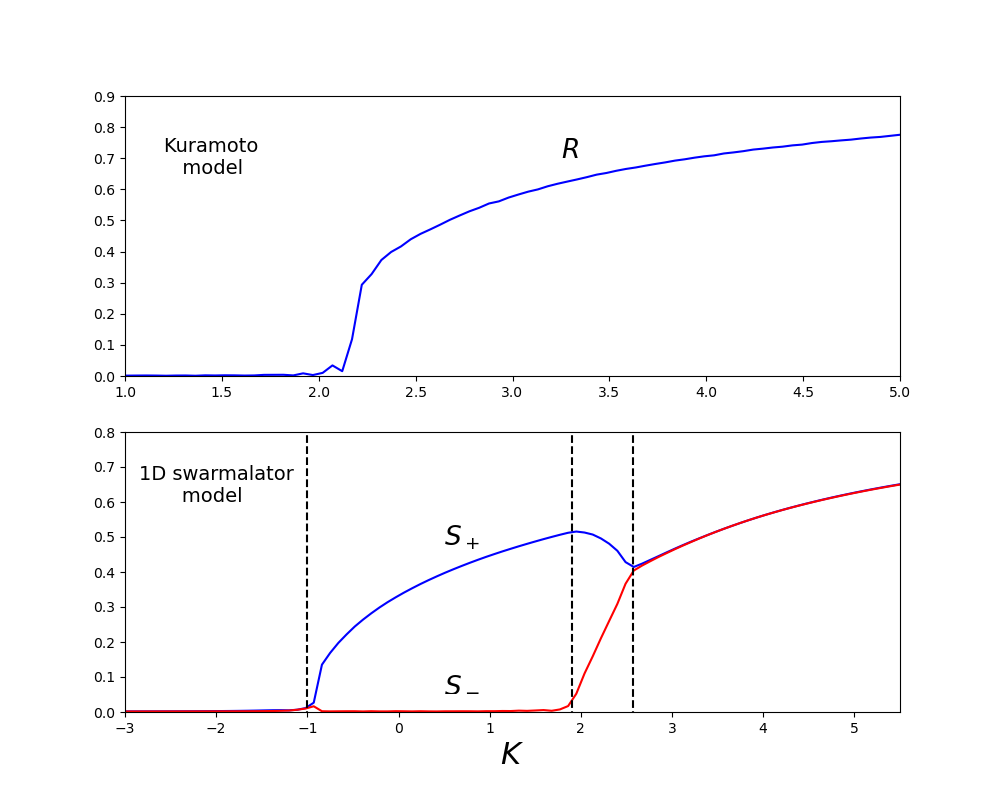
The figure to the right compares the bifurcations of the Kuramoto model to those of the 1D swarmalator model. For the Kuramoto model (top row), the sync order parameter bifurcates from the async state () and then increases monontonically in the sync state (). For the 1D swarmalator model, the bifurcations are richer. Starting with the phase coupling and increasing, bifurcate from the async state () to the phase wave () then to the mixed state () before finally ending up in the sync state (). Note we have taken without loss of generality and are constants that depend on . Expressions for have been worked out, those for in the mixed state are unknown (see ref 5.
For unimodal distribution of such as the Cauchy distribution, the model exhibits four collective states depicted in the figure on the right.
* Async or state. Swarmalators do not exhibit any coherence either in space or phase, being distributed uniformly in position and phase. This state is characterized by the absence of any synchronization or spatial clustering among the swarmalators, as reflected by the zero values of both order parameters .
* Phase wave or state. In the phase wave state, swarmalators form a band or wave pattern with the position and phase are correlated. The wave can either run clockwise or counterclockwise.
* Mixed or state. Swaramlators again form a phase wave, but now the wave is distorted, forming two rough clusters; thus it is the a mixture of the phase wave and the sync state (described next).
* Sync or state. Swarmalators form two synchronous cluster in both space and phase. Single cluster states are formed for some initial conditions.
Note in each state, the swarmalators split into a locked/drifting sub-populations, just like the Kuramoto model. The locked population are the denser regions in the Figure, the drifters the light grey regions.
The figure to the right compares the bifurcations of the Kuramoto model to those of the 1D swarmalator model. For the Kuramoto model (top row), the sync order parameter bifurcates from the async state () and then increases monontonically in the sync state (). For the 1D swarmalator model, the bifurcations are richer. Starting with the phase coupling and increasing, bifurcate from the async state () to the phase wave () then to the mixed state () before finally ending up in the sync state (). Note we have taken without loss of generality and are constants that depend on . Expressions for have been worked out, those for in the mixed state are unknown (see ref 5.
synchronize
Synchronization is the coordination of events to operate a system in unison. For example, the conductor of an orchestra keeps the orchestra synchronized or ''in time''. Systems that operate with all parts in synchrony are said to be synchrono ...
in time. They were introduced to model the diverse real-world systems which both sync and swarm, such as vinegar eels, magnetic domain walls, and Japanese tree frogs. More formally, they are dynamical units with spatial degrees of freedom and internal degrees of freedom whose dynamics are coupled.
Real world examples
Swarmalation occurs in diverse parts of Nature and technology some of which are discussed below. The Figure to the right plots some examples in a (discipline, number of particles) plot. Biological microswimmers.
Biological microswimmers. Sperm
Sperm (: sperm or sperms) is the male reproductive Cell (biology), cell, or gamete, in anisogamous forms of sexual reproduction (forms in which there is a larger, female reproductive cell and a smaller, male one). Animals produce motile sperm ...
, vinegar eels and potentially other swimmers such as C elegans swarm through space via the rhythmic beating of their tails. This beating may synchronize with the beating of a neighboring swimmer via hydrodynamic coupling, which in turn causes spatial attraction; sync links to self-assembly. This can lead to vortex arrays, trains metachronal waves and other collective effects.
Magnetic domain walls are key features in the field of magnetism and materials science, defined by the boundary between different magnetic domains
A magnetic domain is a region within a magnetic material in which the magnetization is in a uniform direction. This means that the individual magnetic moments of the atoms are aligned with one another and they point in the same direction. When c ...
in ferromagnetic
Ferromagnetism is a property of certain materials (such as iron) that results in a significant, observable magnetic permeability, and in many cases, a significant magnetic coercivity, allowing the material to form a permanent magnet. Ferromagne ...
materials. These domains are regions within a material where the magnetic moments of atoms are aligned in the same direction, creating a uniform magnetic field. The hold great promise as memory devices in next generation spintronics
Spintronics (a portmanteau meaning spin transport electronics), also known as spin electronics, is the study of the intrinsic spin of the electron and its associated magnetic moment, in addition to its fundamental electronic charge, in solid-st ...
. In a simplified model, a domain wall can be described by its center of mass and the in-plane angle of its magnetic dipole vector, thereby classifying them as swarmalators. Experiments reveal that the interaction between two such domain walls leads to rich spatiotemporal behaviors some of which is captured by the 1D swarmalator model listed above.
Japanese Tree frogs. During courtship rituals, male Japanese Tree frogs attract the attention of females by croaking rhythmically. Neighboring males tend to alternate the croaking (croak degree out of phase) so as to avoid "speaking over each other". Evidence suggests this (anti)-synchronization influences the inter-frog spatial dynamics, making them swarmalators.
Janus particles
Janus particles are special types of nanoparticles or microparticles whose surfaces have two or more distinct physical property, physical properties. This unique surface of Janus particles allows two different types of chemistry to occur on the s ...
are spherical particles with one hemisphere coated in a magnetic substance, the other remaining non-magnetic. They are named after the Roman God Janus
In ancient Roman religion and myth, Janus ( ; ) is the god of beginnings, gates, transitions, time, duality, doorways, passages, frames, and endings. He is usually depicted as having two faces. The month of January is named for Janus (''Ianu ...
who has two faces. This anisotropy gives the particles unusual magnetic properties. When subject to external magnetic fields, their magnetic dipoles vectors begins to oscillate which induces and couples to movements (thus qualifying as a swarmalators). The resultant "sync-selected self-assembly" gives rise novel superstructure with potential use in biomedicine contexts such as targeted drug delivery, bio imaging, and bio-sensing.
Quincke rollers are a class of active particle that exhibits self-propelled motion in a fluid due to an electrohydrodynamic phenomenon known as the Quincke effect. This effect occurs when a dielectric (non-conducting) particle is subject to an electric field. The rotation of the particle, combined with frictional interactions with the surrounding fluid and surface, leads to a rolling motion. Thus, the particle has a phase and a position which couple, as required of swarmalator. Collections of Quincke rollers produce rich emergent behavior such as activity waves
and shock waves.
Embryonic cells are the foundational building blocks of an embryo, undergoing division and differentiation to form the complex structures of an organism. These cells exhibit remarkable plasticity, allowing them to transform into a wide range of specialized cell types. In the context of swarmalators, embryonic cells display a unique blend of synchronization and swarming behaviors. They coordinate their movements and genetic expression patterns in response to various cues, a process essential for proper tissue formation and organ development. This linking of sync and self-assembly make embryonic cells a compelling example of a real-world swarmalators.
Robot swarms. Land based rovers as well as aerial drones programmed with swarmalator models have been created and has recreated the five collective states of the swarmalator model (see Mathematical Models section for the plot of these states). The linking of sync and swarming defines a new kind of bio-inspired algorithm which several potential applications.
2D swarmalator model
A mathematical model for swarmalators moving in 2D has been proposed. This 2D swarmalator model in generic form is : The spatial dynamics combine pairwise interaction with pairwise , which produces swarming / aggregation. The novelty is the attraction is modified by a phase term ; thus the aggregation becomes phase-dependent. Likewise, the phase dynamics contain a sync term modified by a spatial term so the synchronization becomes position dependent. In short, the swarmalators model the interaction between self-synchronization and self-assembly in space. While in general the position could be in 2D or 3D, the instance of the swarmalator model originally introduced is a 2D model and the choices for etc. were : There are two parameters and are parameters: controls the strength of phase-space attraction/repulsion, while describes the phase coupling strength. The above can be considered a blending of the aggregation model introduced from biological swarming (the spatial part) and theKuramoto model
The Kuramoto model (or Kuramoto–Daido model), first proposed by , is a mathematical model used in describing synchronization. More specifically, it is a model for the behavior of a large set of coupled oscillators. Its formulation was motivated b ...
of phase oscillators (the phase part).
Phenomena
 The model above produces five collective states depicted in Figure 1:
* Static sync: Swarmalators form a disk in space and are fully synchronized in phase.
* Static async: Swarmalators form a disk in space and are fully asynchronous in phase.
* Static phase wave: Swarmalators form an annulus in space with a phase wave (e.g. a full color-wheel or rainbow.)
* Splintered phase wave: The phase wave splinters into clusters of synchronous swarmalators. Within each cluster, the swarmalators execute periodic motion in space and phase.
* Active phase wave: Swarmalators run in a space-phase vortex, with half running clockwise and the remaining half running counter-clockwise.
To demarcate where each state arises and disappears as a parameters are changed, the rainbow order parameters,
:
where are used. Figure 2 plots versus for fixed . As can be seen, in the rainbow-like static phased wave state (at = 0), and then declines as decreases. A second order parameter , defined as the fraction of swarmalators that have completed at least one cycle in space and phase after transients in also plotted, which can distinguish between the active phase wave and splintered phase wave states.
The model above produces five collective states depicted in Figure 1:
* Static sync: Swarmalators form a disk in space and are fully synchronized in phase.
* Static async: Swarmalators form a disk in space and are fully asynchronous in phase.
* Static phase wave: Swarmalators form an annulus in space with a phase wave (e.g. a full color-wheel or rainbow.)
* Splintered phase wave: The phase wave splinters into clusters of synchronous swarmalators. Within each cluster, the swarmalators execute periodic motion in space and phase.
* Active phase wave: Swarmalators run in a space-phase vortex, with half running clockwise and the remaining half running counter-clockwise.
To demarcate where each state arises and disappears as a parameters are changed, the rainbow order parameters,
:
where are used. Figure 2 plots versus for fixed . As can be seen, in the rainbow-like static phased wave state (at = 0), and then declines as decreases. A second order parameter , defined as the fraction of swarmalators that have completed at least one cycle in space and phase after transients in also plotted, which can distinguish between the active phase wave and splintered phase wave states.
Puzzles
There are several unresolved puzzles and open questions related to swarmalators: * Melting point : What is the value at which the static async state melts into the active phase wave state? * Splitting point : What is the splitting point at which the active phase wave splits into the splintered phase wave? * Rainbow order parameters: Can you derive an expression for the supercritical branch of the for fixed in the active phase wave and splintered phase wave states? * : What determines the number of clusters formed in the splintered phase wave?1D swarmalator model
A simpler swarmalator model where the spatial motion is confined to a 1D ring has also been proposedYoon, S., et al. "Sync and Swarm: Solvable Model of Nonidentical Swarmalators." Physical Review Letters 129.20 (2022): 208002. : where are the (random) natural frequencies of the i-th swarmalator and are drawn from certain distributions . This 1D model corresponds to the angular component of the 2D swarmalator model. The restriction to this simpler topology allows for a greater analysis. For instance, the model with natural frequencies can be solved by defining the sum/difference coordinates the model simplifies into a pair of linearly coupled Kuramoto models : where , and the rainbow order parameters are the equivalent of the 2D model :
 For unimodal distribution of such as the Cauchy distribution, the model exhibits four collective states depicted in the figure on the right.
* Async or state. Swarmalators do not exhibit any coherence either in space or phase, being distributed uniformly in position and phase. This state is characterized by the absence of any synchronization or spatial clustering among the swarmalators, as reflected by the zero values of both order parameters .
* Phase wave or state. In the phase wave state, swarmalators form a band or wave pattern with the position and phase are correlated. The wave can either run clockwise or counterclockwise.
* Mixed or state. Swaramlators again form a phase wave, but now the wave is distorted, forming two rough clusters; thus it is the a mixture of the phase wave and the sync state (described next).
* Sync or state. Swarmalators form two synchronous cluster in both space and phase. Single cluster states are formed for some initial conditions.
Note in each state, the swarmalators split into a locked/drifting sub-populations, just like the Kuramoto model. The locked population are the denser regions in the Figure, the drifters the light grey regions.
The figure to the right compares the bifurcations of the Kuramoto model to those of the 1D swarmalator model. For the Kuramoto model (top row), the sync order parameter bifurcates from the async state () and then increases monontonically in the sync state (). For the 1D swarmalator model, the bifurcations are richer. Starting with the phase coupling and increasing, bifurcate from the async state () to the phase wave () then to the mixed state () before finally ending up in the sync state (). Note we have taken without loss of generality and are constants that depend on . Expressions for have been worked out, those for in the mixed state are unknown (see ref 5.
For unimodal distribution of such as the Cauchy distribution, the model exhibits four collective states depicted in the figure on the right.
* Async or state. Swarmalators do not exhibit any coherence either in space or phase, being distributed uniformly in position and phase. This state is characterized by the absence of any synchronization or spatial clustering among the swarmalators, as reflected by the zero values of both order parameters .
* Phase wave or state. In the phase wave state, swarmalators form a band or wave pattern with the position and phase are correlated. The wave can either run clockwise or counterclockwise.
* Mixed or state. Swaramlators again form a phase wave, but now the wave is distorted, forming two rough clusters; thus it is the a mixture of the phase wave and the sync state (described next).
* Sync or state. Swarmalators form two synchronous cluster in both space and phase. Single cluster states are formed for some initial conditions.
Note in each state, the swarmalators split into a locked/drifting sub-populations, just like the Kuramoto model. The locked population are the denser regions in the Figure, the drifters the light grey regions.
The figure to the right compares the bifurcations of the Kuramoto model to those of the 1D swarmalator model. For the Kuramoto model (top row), the sync order parameter bifurcates from the async state () and then increases monontonically in the sync state (). For the 1D swarmalator model, the bifurcations are richer. Starting with the phase coupling and increasing, bifurcate from the async state () to the phase wave () then to the mixed state () before finally ending up in the sync state (). Note we have taken without loss of generality and are constants that depend on . Expressions for have been worked out, those for in the mixed state are unknown (see ref 5.
References
{{Reflist Mathematical modeling