sprouts (game) on:
[Wikipedia]
[Google]
[Amazon]
Sprouts is an impartial
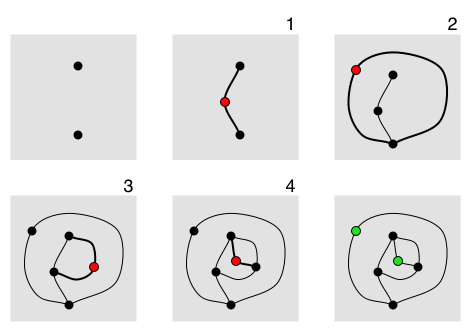 The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules:
* The line may be straight or curved, but must not touch or cross itself or any other line.
* The new spot cannot be placed on top of one of the endpoints of the new line. Thus the new spot splits the line into two shorter lines.
* No spot may have more than three lines attached to it. For the purposes of this rule, a line from the spot to itself counts as two attached lines and new spots are counted as having two lines already attached to them.
* You cannot touch a dot twice with one line then connect it to another.
In so-called ''normal play'', the player who makes the last move wins. In ''
The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules:
* The line may be straight or curved, but must not touch or cross itself or any other line.
* The new spot cannot be placed on top of one of the endpoints of the new line. Thus the new spot splits the line into two shorter lines.
* No spot may have more than three lines attached to it. For the purposes of this rule, a line from the spot to itself counts as two attached lines and new spots are counted as having two lines already attached to them.
* You cannot touch a dot twice with one line then connect it to another.
In so-called ''normal play'', the player who makes the last move wins. In ''
 Each spot starts with three ''lives'' and each move reduces the total number of lives in the game by one (two lives are lost at the ends of the line, but the new spot has one life). So at the end of the game there are remaining lives. Each surviving spot has only one life (otherwise there would be another move joining that spot to itself), so there are exactly survivors. There must be at least one survivor, namely the spot added in the final move. So ; hence a game can last no more than 3''n'' − 1 moves.
This upper bound is actually the maximum, and it can be attained in many ways by ensuring that there is only one survivor at the end of the game. For instance, the game on the right has one survivor and 3''n'' − 1 moves.
Each spot starts with three ''lives'' and each move reduces the total number of lives in the game by one (two lives are lost at the ends of the line, but the new spot has one life). So at the end of the game there are remaining lives. Each surviving spot has only one life (otherwise there would be another move joining that spot to itself), so there are exactly survivors. There must be at least one survivor, namely the spot added in the final move. So ; hence a game can last no more than 3''n'' − 1 moves.
This upper bound is actually the maximum, and it can be attained in many ways by ensuring that there is only one survivor at the end of the game. For instance, the game on the right has one survivor and 3''n'' − 1 moves.
Julien Lemoine and Simon Viennot web site The normal-play results so far are all consistent with the conjecture of Applegate, Jacobson, and Sleator.
 A variant of the game, named Brussels Sprouts after the cruciferous vegetable, starts with a number of crosses, i.e. spots with four free ends. Each move involves joining two free ends with a curve, again not crossing any existing line, and then putting a short stroke across the line to create two new free ends. This game is finite, and the total number of moves (and thus the game's winner) is predetermined by the initial number of crosses: the players cannot affect the result by their play. Thus, this variant may be termed, after Conway's categorisation of mathematics itself, a "one player game".
Each move removes two free ends and introduces two more. Nonetheless, the game is bound to end as some free ends become isolated. With ''n'' initial crosses, the number of moves will, remarkably, always be 5''n'' − 2. Consequently, a game starting with an odd number of crosses will be a first player win, while a game starting with an even number will be a second player win regardless of the moves.
To prove this, first, we argue the game must end. Then, we will calculate precisely how many moves it needs to end. The game outcome is then implied, as already described.
Treat each cross as a
A variant of the game, named Brussels Sprouts after the cruciferous vegetable, starts with a number of crosses, i.e. spots with four free ends. Each move involves joining two free ends with a curve, again not crossing any existing line, and then putting a short stroke across the line to create two new free ends. This game is finite, and the total number of moves (and thus the game's winner) is predetermined by the initial number of crosses: the players cannot affect the result by their play. Thus, this variant may be termed, after Conway's categorisation of mathematics itself, a "one player game".
Each move removes two free ends and introduces two more. Nonetheless, the game is bound to end as some free ends become isolated. With ''n'' initial crosses, the number of moves will, remarkably, always be 5''n'' − 2. Consequently, a game starting with an odd number of crosses will be a first player win, while a game starting with an even number will be a second player win regardless of the moves.
To prove this, first, we argue the game must end. Then, we will calculate precisely how many moves it needs to end. The game outcome is then implied, as already described.
Treat each cross as a
The Complete (?) List of References for the Game of Sprouts
''World Game of Sprouts Association.''
Danny Purvis, association of Sprouts players
The Game of Sprouts
at
SproutsWiki
web site of Julien Lemoine and Simon Viennot, with the source code and binaries of their program Mathematical games Paper-and-pencil games John Horton Conway
paper-and-pencil game
Paper-and-pencil games or paper-and-pen games (or some variation on those terms) are games that can be played solely with paper and pencil, pencils (or other writing implements), usually without erasing. They may be played to pass the time, as ...
which can be analyzed for its mathematical
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
properties. It was invented by mathematicians John Horton Conway
John Horton Conway (26 December 1937 – 11 April 2020) was an English mathematician. He was active in the theory of finite groups, knot theory, number theory, combinatorial game theory and coding theory. He also made contributions to many b ...
and Michael S. Paterson at Cambridge University
The University of Cambridge is a Public university, public collegiate university, collegiate research university in Cambridge, England. Founded in 1209, the University of Cambridge is the List of oldest universities in continuous operation, wo ...
in the early 1960s. The setup is even simpler than the popular dots and boxes
Dots and boxes is a pencil-and-paper game for two players (sometimes more). It was first published in the 19th century by French mathematician Édouard Lucas, who called it . It has gone by many other names, including dots and dashes, game of do ...
game, but gameplay develops much more artistically and organically.
Rules
 The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules:
* The line may be straight or curved, but must not touch or cross itself or any other line.
* The new spot cannot be placed on top of one of the endpoints of the new line. Thus the new spot splits the line into two shorter lines.
* No spot may have more than three lines attached to it. For the purposes of this rule, a line from the spot to itself counts as two attached lines and new spots are counted as having two lines already attached to them.
* You cannot touch a dot twice with one line then connect it to another.
In so-called ''normal play'', the player who makes the last move wins. In ''
The game is played by two players, starting with a few spots drawn on a sheet of paper. Players take turns, where each turn consists of drawing a line between two spots (or from a spot to itself) and adding a new spot somewhere along the line. The players are constrained by the following rules:
* The line may be straight or curved, but must not touch or cross itself or any other line.
* The new spot cannot be placed on top of one of the endpoints of the new line. Thus the new spot splits the line into two shorter lines.
* No spot may have more than three lines attached to it. For the purposes of this rule, a line from the spot to itself counts as two attached lines and new spots are counted as having two lines already attached to them.
* You cannot touch a dot twice with one line then connect it to another.
In so-called ''normal play'', the player who makes the last move wins. In ''misère play
Misère ( French for "destitution"), misere, nullo, bettel, betl, or (German for "beggar"; equivalent terms in other languages include , and ) is a bid in various card games, and the player who bids misère undertakes to win no tricks or as f ...
'', the player who makes the last move loses. Misère Sprouts is perhaps the only misère combinatorial game that is played competitively in an organized forum.
The diagram on the right shows a 2-spot game of normal-play Sprouts. After the fourth move, most of the spots are ''dead''–they have three lines attached to them, so they cannot be used as endpoints for a new line. There are two spots (shown in green) that are still ''alive'', having fewer than three lines attached. However, it is impossible to make another move, because a line from a live spot to itself would make four attachments, and a line from one live spot to the other would cross lines. Therefore, no fifth move is possible, and the first player loses. Live spots at the end of the game are called ''survivors'' and play a key role in the analysis of Sprouts.
Number of moves
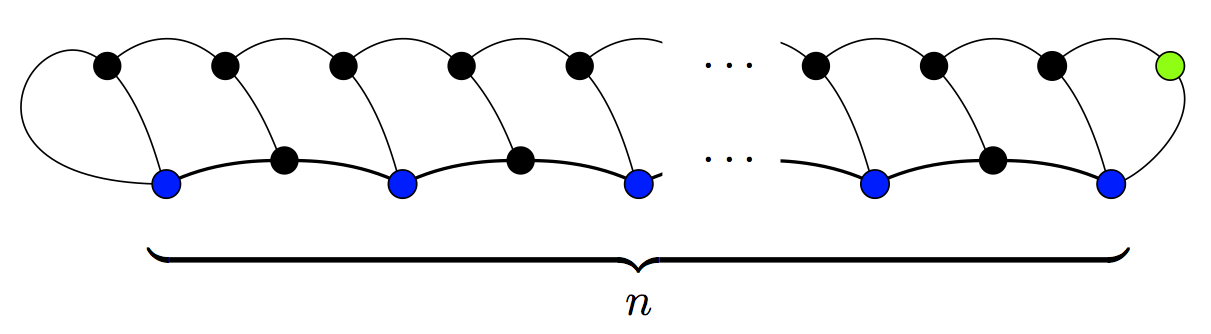
The game of Sprouts always terminates, although this fact is not evident from the game rules, since the number of spots increases at each move. The approach to understand why the game always terminates is to consider the number of ''lives'' (opportunities to connect a line) instead of the number of spots. Then, it can be shown that if the game starts with ''n'' spots, it will end in no more than 3''n'' − 1 moves and no fewer than 2''n'' moves. In the following proofs, it is assumed that a game starts with ''n'' spots and lasts for exactly ''m'' moves.Maximum number of moves
 Each spot starts with three ''lives'' and each move reduces the total number of lives in the game by one (two lives are lost at the ends of the line, but the new spot has one life). So at the end of the game there are remaining lives. Each surviving spot has only one life (otherwise there would be another move joining that spot to itself), so there are exactly survivors. There must be at least one survivor, namely the spot added in the final move. So ; hence a game can last no more than 3''n'' − 1 moves.
This upper bound is actually the maximum, and it can be attained in many ways by ensuring that there is only one survivor at the end of the game. For instance, the game on the right has one survivor and 3''n'' − 1 moves.
Each spot starts with three ''lives'' and each move reduces the total number of lives in the game by one (two lives are lost at the ends of the line, but the new spot has one life). So at the end of the game there are remaining lives. Each surviving spot has only one life (otherwise there would be another move joining that spot to itself), so there are exactly survivors. There must be at least one survivor, namely the spot added in the final move. So ; hence a game can last no more than 3''n'' − 1 moves.
This upper bound is actually the maximum, and it can be attained in many ways by ensuring that there is only one survivor at the end of the game. For instance, the game on the right has one survivor and 3''n'' − 1 moves.

Minimum number of moves
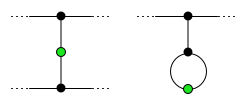
At the end of the game, a dead spot is called the ''neighbor'' of a survivor if it is either adjacent to that survivor or, if the survivor has a loop, it is adjacent to a spot adjacent to the survivor. This is illustrated in the diagram to the right. Each survivor has exactly two dead neighbors. No dead spot can be the neighbor of two different survivors, for otherwise there would be a move joining the survivors. All other dead spots (not neighbors of a survivor) are called ''pharisees'' (from theHebrew
Hebrew (; ''ʿÎbrit'') is a Northwest Semitic languages, Northwest Semitic language within the Afroasiatic languages, Afroasiatic language family. A regional dialect of the Canaanite languages, it was natively spoken by the Israelites and ...
for " separated ones"). Suppose there are ''p'' pharisees. Then
:
since initial spots + moves = total spots at end of game = survivors + neighbors + pharisees. Rearranging gives:
:
Consequently, a game lasts for at least 2''n'' moves, and the number of pharisees is divisible
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a '' multiple'' of m. An integer n is divisible or evenly divisibl ...
by 4.
This lower bound on the length of a game is actually the minimum. The diagram on the right shows a completed game of 2''n'' moves. It has ''n'' survivors, 2''n'' neighbors and 0 pharisees.
Importance in real games
Real games seem to turn into a battle over whether the number of moves will be ''k'' or ''k'' + 1 with other possibilities being quite unlikely. One player tries to create enclosed regions containing survivors (thus reducing the total number of moves that will be played) and the other tries to create pharisees (thus increasing the number of moves that will be played).Winning strategies
Since Sprouts is a finite game where no draw is possible, a perfect strategy exists either for the first or the second player, depending on the number of initial spots. The main question about a given starting position is then to determine which player can force a win if they play perfectly. When thewinning strategy
Determinacy is a subfield of game theory and set theory that examines the conditions under which one or the other player of a game has a winning strategy, and the consequences of the existence of such strategies. Alternatively and similarly, "dete ...
is for the first player, it is said that the ''outcome'' of the position is a "win", and when the winning strategy is for the second player, it is said that the outcome of the position is a "loss" (because it is a loss from the point of view of the first player).
The outcome is determined by developing the game tree
In the context of combinatorial game theory, a game tree is a graph representing all possible game states within a sequential game that has perfect information. Such games include chess, checkers, Go, and tic-tac-toe.
A game tree can be us ...
of the starting position. This can be done by hand only for a small number of spots, and all the new results since 1990 have been obtained by extensive search with computers.
Normal version
'' Winning Ways for your Mathematical Plays'' reports that the 6-spot normal game was proved to be a win for the second player by Denis Mollison, with a hand-made analysis of 47 pages. It stood as the record for a long time, until the first computer analysis, which was done atCarnegie Mellon University
Carnegie Mellon University (CMU) is a private research university in Pittsburgh, Pennsylvania, United States. The institution was established in 1900 by Andrew Carnegie as the Carnegie Technical Schools. In 1912, it became the Carnegie Institu ...
in 1990 by David Applegate
David L. Applegate is an American computer scientist known for his research on the traveling salesperson problem.
Education
Applegate graduated from the University of Dayton in 1984, and completed his doctorate in 1991 from Carnegie Mellon U ...
, Guy Jacobson, and Daniel Sleator
Daniel Dominic Kaplan Sleator (born 10 December 1953) is a professor of computer science at Carnegie Mellon University, Pittsburgh, United States. In 1999, he won the ACM Paris Kanellakis Award (jointly with Robert Tarjan) for the splay tree d ...
. They reached up to 11 spots with some of the best hardware available at the time.
Applegate, Jacobson and Sleator observed a pattern in their results, and conjecture
In mathematics, a conjecture is a conclusion or a proposition that is proffered on a tentative basis without proof. Some conjectures, such as the Riemann hypothesis or Fermat's conjecture (now a theorem, proven in 1995 by Andrew Wiles), ha ...
d that the first player has a winning strategy when the number of spots divided by six leaves a remainder of three, four, or five. This is a mathematical way of saying that the pattern displayed by the outcome in the table below repeats itself indefinitely, with a period of six spots.
In 2001, Riccardo Focardi and Flamina Luccio described a method to prove by hand that the normal 7-spot game is a loss.
Then, the computation results were extended in 2006 by Josh Jordan up to 14 spots. In 2007, Julien Lemoine and Simon Viennot introduced an algorithm based on the concept of nimber
In mathematics, the nimbers, also called Grundy numbers (not to be confused with Grundy chromatic numbers), are introduced in combinatorial game theory, where they are defined as the values of heaps in the game Nim. The nimbers are the ordin ...
s to accelerate the computation, reaching up to 32 spots. They have extended the computation up to 44 spots in 2011, and three isolated starting positions, with 46, 47 and 53 spots.Computation records of normal and misère SproutsJulien Lemoine and Simon Viennot web site The normal-play results so far are all consistent with the conjecture of Applegate, Jacobson, and Sleator.
Misère version
The computation history of the misère version of Sprouts is very similar to that of the normal version, with the same people involved. However, the misère version is more difficult to compute, and progress has been significantly slower. In 1990, Applegate, Jacobson and Sleator reached up to nine spots. Based on their results, they conjectured that the outcome follows a regular pattern of period five. However, this conjecture was invalidated in 2007 when Josh Jordan and Roman Khorkov extended the misère analysis up to 12 spots: the 12-spot misère game is a win, and not the conjectured loss. The same team reached up to 16 spots in 2009. The same year, Julien Lemoine and Simon Viennot reached 17 spots with complicated algorithms. They were able to extend their analysis up to 20 points in 2011. The results for misère play are now conjectured to follow a pattern of length six with some exceptional values: the first player wins in misère Sprouts when the remainder (mod
Mod, MOD or mods may refer to:
Places
* Modesto City–County Airport, Stanislaus County, California, US
Arts, entertainment, and media Music
* Mods (band), a Norwegian rock band
* M.O.D. (Method of Destruction), a band from New York City, US
* ...
6) is zero, four, or five, except that the first player wins the one-spot game and loses the four-spot game. The table below shows the pattern, with the two irregular values in bold.
Brussels Sprouts
 A variant of the game, named Brussels Sprouts after the cruciferous vegetable, starts with a number of crosses, i.e. spots with four free ends. Each move involves joining two free ends with a curve, again not crossing any existing line, and then putting a short stroke across the line to create two new free ends. This game is finite, and the total number of moves (and thus the game's winner) is predetermined by the initial number of crosses: the players cannot affect the result by their play. Thus, this variant may be termed, after Conway's categorisation of mathematics itself, a "one player game".
Each move removes two free ends and introduces two more. Nonetheless, the game is bound to end as some free ends become isolated. With ''n'' initial crosses, the number of moves will, remarkably, always be 5''n'' − 2. Consequently, a game starting with an odd number of crosses will be a first player win, while a game starting with an even number will be a second player win regardless of the moves.
To prove this, first, we argue the game must end. Then, we will calculate precisely how many moves it needs to end. The game outcome is then implied, as already described.
Treat each cross as a
A variant of the game, named Brussels Sprouts after the cruciferous vegetable, starts with a number of crosses, i.e. spots with four free ends. Each move involves joining two free ends with a curve, again not crossing any existing line, and then putting a short stroke across the line to create two new free ends. This game is finite, and the total number of moves (and thus the game's winner) is predetermined by the initial number of crosses: the players cannot affect the result by their play. Thus, this variant may be termed, after Conway's categorisation of mathematics itself, a "one player game".
Each move removes two free ends and introduces two more. Nonetheless, the game is bound to end as some free ends become isolated. With ''n'' initial crosses, the number of moves will, remarkably, always be 5''n'' − 2. Consequently, a game starting with an odd number of crosses will be a first player win, while a game starting with an even number will be a second player win regardless of the moves.
To prove this, first, we argue the game must end. Then, we will calculate precisely how many moves it needs to end. The game outcome is then implied, as already described.
Treat each cross as a graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discret ...
with 5 vertices and 4 edges. In the starting position with ''n'' crosses, we have a planar graph
In graph theory, a planar graph is a graph (discrete mathematics), graph that can be graph embedding, embedded in the plane (geometry), plane, i.e., it can be drawn on the plane in such a way that its edges intersect only at their endpoints. ...
with ''v'' = 5''n'' vertices, ''e'' = 4''n'' edges, ''f'' = 1 face, and ''k'' = ''n'' connected components. The Euler characteristic for connected planar graphs is 2. In a disconnected planar graph, we get
After ''m'' moves, we have:
* ''e'' = 4''n'' + 4''m'' since at each move, the player adds 4 edges.
* ''v'' = 5''n'' + 3''m'' since at each move, the player adds 3 vertices.
Then by the above, we have
* ''f'' − ''k'' = 1 + ''e'' − ''v'' = 1 − ''n'' + ''m''
Next, note that every time we add a cross, we are ensuring that each side of this cross ends up with a degree 1 vertex. Thus, throughout the game, every face has at least one degree 1 vertex. Yet, the number of degree 1 vertices is invariant throughout the game, and remains at 4''n''. Hence, ''f'' is at most 4''n''.
From this, we see ''m'' = ''f'' − ''k'' − 1 + ''n'' is at most (since ''k'' is at least 1 and ''f'' is at most 4''n''). So the game must terminate, and it must terminate in at most moves. Now, we argue it must terminate in exactly moves.
In the final configuration, no face can have more than one degree 1 vertex, since otherwise, we could connect them with a cross and there would still be a legal move. Every face has at least one such vertex, so it must end with exactly one such vertex. So in the final configuration, ''f'' is exactly 4''n''.
Similarly, in the final configuration, the graph must be connected, since the outer face gets at least one degree 1 vertex per connected component, and cannot have more than one such vertex. So, in the final configuration, ''k'' is exactly 1.
Thus, to obtain the final configuration, we must have had ''m'' = ''f''−''k''−1+''n'' = 4''n''−1−1+''n'' = 5''n''−2.
A combination of standard Sprouts and Brussels Sprouts can also be played. The game starts with an arbitrary number (''n'') of dots or crosses. At each turn, the player chooses to add either a dot, or a cross, along the line they have just drawn. The duration of the game lays between (2''n'') and (), depending on the number of dots or crosses having been added.
For ''n'' = 1, starting with a dot, the game will end after 2 moves. Starting with a cross, it will end after 2 moves if the first player adds a dot, after 3 moves if they add a cross: hence the first player has a winning strategy for both the normal and the misère version. For ''n'' > 1, the analysis is not completed.
References
Bibliography * Elwyn R. Berlekamp, John Conway and Richard K. Guy, '' Winning Ways for your Mathematical Plays'', 1992. * . * * Mackenzie, Dana, "Answers to Sprouts", Cornell University Math Department, 2003-2004, {{cite web , url=https://pi.math.cornell.edu/~mec/2003-2004/graphtheory/sprouts/answerstosprouts3.html.External links
The Complete (?) List of References for the Game of Sprouts
''World Game of Sprouts Association.''
Danny Purvis, association of Sprouts players
The Game of Sprouts
at
University of Utah
The University of Utah (the U, U of U, or simply Utah) is a public university, public research university in Salt Lake City, Utah, United States. It was established in 1850 as the University of Deseret (Book of Mormon), Deseret by the General A ...
, with an interactive applet for human-vs-human play. (Requires Java)
SproutsWiki
web site of Julien Lemoine and Simon Viennot, with the source code and binaries of their program Mathematical games Paper-and-pencil games John Horton Conway