snub (geometry) on:
[Wikipedia]
[Google]
[Amazon]

 In
In
 There is only one uniform convex snub in 4-dimensions, the
There is only one uniform convex snub in 4-dimensions, the 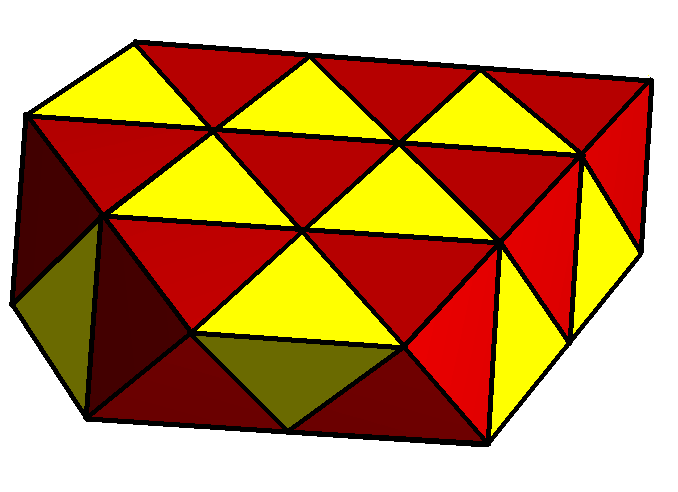 Another Euclidean (scaliform) honeycomb is an alternated square slab honeycomb, s, and or sr and :
:
Another Euclidean (scaliform) honeycomb is an alternated square slab honeycomb, s, and or sr and :
:  The only uniform snub hyperbolic uniform honeycomb is the ''snub hexagonal tiling honeycomb'', as s and , which can also be constructed as an alternated hexagonal tiling honeycomb, h, . It is also constructed as s and .
Another hyperbolic (scaliform) honeycomb is a snub order-4 octahedral honeycomb, s, and .
The only uniform snub hyperbolic uniform honeycomb is the ''snub hexagonal tiling honeycomb'', as s and , which can also be constructed as an alternated hexagonal tiling honeycomb, h, . It is also constructed as s and .
Another hyperbolic (scaliform) honeycomb is a snub order-4 octahedral honeycomb, s, and .
Googlebook
** (Paper 17) Harold Scott MacDonald Coxeter, Coxeter, ''The Evolution of Coxeter–Dynkin diagrams'', ieuw Archief voor Wiskunde 9 (1991) 233–248** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380–407, MR 2,10** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559–591** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3–45* Harold Scott MacDonald Coxeter, Coxeter, ''The Beauty of Geometry: Twelve Essays'', Dover Publications, 1999, (Chapter 3: Wythoff's Construction for Uniform Polytopes) * Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 * John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, * {{mathworld , urlname = Snubification , title = Snubification * Richard Klitzing, ''Snubs, alternated facetings, and Stott–Coxeter–Dynkin diagrams'', Symmetry: Culture and Science, Vol. 21, No.4, 329–344, (2010
Geometry Snub tilings
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a snub is an operation applied to a polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal Face (geometry), faces, straight Edge (geometry), edges and sharp corners or Vertex (geometry), vertices. The term "polyhedron" may refer ...
. The term originates from Kepler
Johannes Kepler (27 December 1571 – 15 November 1630) was a German astronomer, mathematician, astrologer, natural philosopher and writer on music. He is a key figure in the 17th-century Scientific Revolution, best known for his laws of p ...
's names of two Archimedean solid
The Archimedean solids are a set of thirteen convex polyhedra whose faces are regular polygon and are vertex-transitive, although they aren't face-transitive. The solids were named after Archimedes, although he did not claim credit for them. They ...
s, for the snub cube () and snub dodecahedron
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex Isogonal figure, isogonal nonprismatic solids constructed by two or more types of regular polygon Face (geometry), faces.
The snub dod ...
().
In general, snubs have chiral symmetry with two forms: with clockwise or counterclockwise orientation. By Kepler's names, a snub can be seen as an expansion of a regular polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In ...
: moving the faces apart, twisting them about their centers, adding new polygons centered on the original vertices, and adding pairs of triangles fitting between the original edges.
The terminology was generalized by Coxeter, with a slightly different definition, for a wider set of uniform polytopes.
Conway snubs
John Conway explored generalized polyhedron operators, defining what is now called Conway polyhedron notation, which can be applied to polyhedra and tilings. Conway calls Coxeter's operation a ''semi-snub''. In this notation, snub is defined by the dual and gyro operators, as ''s'' = ''dg'', and it is equivalent to an alternation of a truncation of an ambo operator. Conway's notation itself avoids Coxeter's alternation (half) operation since it only applies for polyhedra with even-sided faces. In 4-dimensions, Conway suggests thesnub 24-cell
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular Tetrahedron, tetrahedral and 24 Regular icosahedron, icosahedral cell (mathematics), cells. Five tetrahedra and three icosahedra meet ...
should be called a ''semi-snub 24-cell'' because, unlike 3-dimensional snub polyhedra are alternated omnitruncated forms, it is not an alternated omnitruncated 24-cell. It is instead actually an alternated truncated 24-cell.Conway, 2008, p.401 Gosset's Semi-snub Polyoctahedron
Coxeter's snubs, regular and quasiregular
Coxeter's snub terminology is slightly different, meaning an alternatedtruncation
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point.
Truncation and floor function
Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathbb ...
, deriving the snub cube as a ''snub cuboctahedron'', and the snub dodecahedron
In geometry, the snub dodecahedron, or snub icosidodecahedron, is an Archimedean solid, one of thirteen convex Isogonal figure, isogonal nonprismatic solids constructed by two or more types of regular polygon Face (geometry), faces.
The snub dod ...
as a ''snub icosidodecahedron
In geometry, an icosidodecahedron or pentagonal gyrobirotunda is a polyhedron with twenty (''icosi-'') triangular faces and twelve (''dodeca-'') pentagonal faces. An icosidodecahedron has 30 identical Vertex (geometry), vertices, with two triang ...
''. This definition is used in the naming of two Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s: the snub disphenoid
In geometry, the snub disphenoid is a convex polyhedron with 12 equilateral triangles as its face (geometry), faces. It is an example of deltahedron and Johnson solid. It can be constructed in different approaches. This shape is also called Siame ...
and the snub square antiprism, and of higher dimensional polytopes, such as the 4-dimensional snub 24-cell
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular Tetrahedron, tetrahedral and 24 Regular icosahedron, icosahedral cell (mathematics), cells. Five tetrahedra and three icosahedra meet ...
, with extended Schläfli symbol s, and Coxeter diagram .
A regular polyhedron
A regular polyhedron is a polyhedron whose symmetry group acts transitive group action, transitively on its Flag (geometry), flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In ...
(or tiling), with Schläfli symbol , and Coxeter diagram , has truncation
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point.
Truncation and floor function
Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathbb ...
defined as , and , and has snub defined as an alternated truncation , and . This alternated construction requires ''q'' to be even.
A quasiregular polyhedron, with Schläfli symbol or ''r'', and Coxeter diagram or , has quasiregular truncation
In mathematics and computer science, truncation is limiting the number of digits right of the decimal point.
Truncation and floor function
Truncation of positive real numbers can be done using the floor function. Given a number x \in \mathbb ...
defined as or ''tr'', and or , and has quasiregular snub defined as an alternated truncated rectification or ''htr'' = ''sr'', and or .
For example, Kepler's snub cube is derived from the quasiregular cuboctahedron, with a vertical Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
, and Coxeter diagram , and so is more explicitly called a snub cuboctahedron, expressed by a vertical Schläfli symbol , and Coxeter diagram . The snub cuboctahedron is the alternation of the ''truncated cuboctahedron'', , and .
Regular polyhedra with even-order vertices can also be snubbed as alternated truncations, like the ''snub octahedron'', as , , is the alternation of the truncated octahedron, , and . The ''snub octahedron'' represents the pseudoicosahedron, a regular icosahedron
In geometry, an icosahedron ( or ) is a polyhedron with 20 faces. The name comes . The plural can be either "icosahedra" () or "icosahedrons".
There are infinitely many non- similar shapes of icosahedra, some of them being more symmetrical tha ...
with pyritohedral symmetry.
The ''snub tetratetrahedron'', as , and , is the alternation of the truncated tetrahedral symmetry form, , and .
Coxeter's snub operation also allows n-antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
s to be defined as or , based on n-prisms or , while is a regular n- hosohedron, a degenerate polyhedron, but a valid tiling on the sphere with digon or lune
Lune may refer to:
Rivers
*River Lune, in Lancashire and Cumbria, England
*River Lune, Durham, in County Durham, England
*Lune (Weser), a 43 km-long tributary of the Weser in Germany
*Lune River (Tasmania), in south-eastern Tasmania, Australia
Pl ...
-shaped faces.
The same process applies for snub tilings:
Examples
Nonuniform snub polyhedra
Nonuniform polyhedra with all even-valance vertices can be snubbed, including some infinite sets; for example:Coxeter's uniform snub star-polyhedra
Snub star-polyhedra are constructed by their Schwarz triangle (p q r), with rational ordered mirror-angles, and all mirrors active and alternated.Coxeter's higher-dimensional snubbed polytopes and honeycombs
In general, a regular polychoron withSchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
, and Coxeter diagram , has a snub with extended Schläfli symbol , and .
A rectified polychoron = r, and has snub symbol = sr, and .
Examples
 There is only one uniform convex snub in 4-dimensions, the
There is only one uniform convex snub in 4-dimensions, the snub 24-cell
In geometry, the snub 24-cell or snub disicositetrachoron is a convex uniform 4-polytope composed of 120 regular Tetrahedron, tetrahedral and 24 Regular icosahedron, icosahedral cell (mathematics), cells. Five tetrahedra and three icosahedra meet ...
. The regular 24-cell
In four-dimensional space, four-dimensional geometry, the 24-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol . It is also called C24, or the icositetrachoron, octaplex (short for "octa ...
has Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines List of regular polytopes and compounds, regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, wh ...
, , and Coxeter diagram , and the snub 24-cell is represented by , Coxeter diagram . It also has an index 6 lower symmetry constructions as or s and , and an index 3 subsymmetry as or sr, and or .
The related snub 24-cell honeycomb can be seen as a or s, and , and lower symmetry or sr and or , and lowest symmetry form as or s and .
A Euclidean honeycomb is an alternated hexagonal slab honeycomb, s, and or sr, and or sr, and .
:  Another Euclidean (scaliform) honeycomb is an alternated square slab honeycomb, s, and or sr and :
:
Another Euclidean (scaliform) honeycomb is an alternated square slab honeycomb, s, and or sr and :
:  The only uniform snub hyperbolic uniform honeycomb is the ''snub hexagonal tiling honeycomb'', as s and , which can also be constructed as an alternated hexagonal tiling honeycomb, h, . It is also constructed as s and .
Another hyperbolic (scaliform) honeycomb is a snub order-4 octahedral honeycomb, s, and .
The only uniform snub hyperbolic uniform honeycomb is the ''snub hexagonal tiling honeycomb'', as s and , which can also be constructed as an alternated hexagonal tiling honeycomb, h, . It is also constructed as s and .
Another hyperbolic (scaliform) honeycomb is a snub order-4 octahedral honeycomb, s, and .
See also
* Snub polyhedronReferences
* * Coxeter, H.S.M. '' Regular Polytopes'', (3rd edition, 1973), Dover edition, (pp. 154–156 8.6 Partial truncation, or alternation) *Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995,Googlebook
** (Paper 17) Harold Scott MacDonald Coxeter, Coxeter, ''The Evolution of Coxeter–Dynkin diagrams'', ieuw Archief voor Wiskunde 9 (1991) 233–248** (Paper 22) H.S.M. Coxeter, ''Regular and Semi Regular Polytopes I'', ath. Zeit. 46 (1940) 380–407, MR 2,10** (Paper 23) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes II'', ath. Zeit. 188 (1985) 559–591** (Paper 24) H.S.M. Coxeter, ''Regular and Semi-Regular Polytopes III'', ath. Zeit. 200 (1988) 3–45* Harold Scott MacDonald Coxeter, Coxeter, ''The Beauty of Geometry: Twelve Essays'', Dover Publications, 1999, (Chapter 3: Wythoff's Construction for Uniform Polytopes) * Norman Johnson ''Uniform Polytopes'', Manuscript (1991) ** N.W. Johnson: ''The Theory of Uniform Polytopes and Honeycombs'', Ph.D. Dissertation, University of Toronto, 1966 * John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, ''The Symmetries of Things'' 2008, * {{mathworld , urlname = Snubification , title = Snubification * Richard Klitzing, ''Snubs, alternated facetings, and Stott–Coxeter–Dynkin diagrams'', Symmetry: Culture and Science, Vol. 21, No.4, 329–344, (2010
Geometry Snub tilings