Signal Automaton

In automata theory, a field of computer science, a signal automaton is a finite automaton extended with a finite set of real-valued clocks. During a run of a signal automaton, clock values increase all with the same speed. Along the transitions of the automaton, clock values can be compared to integers. These comparisons form guards that may enable or disable transitions and by doing so constrain the possible behaviors of the automaton. Further, clocks can be reset.

Example

Before formally defining what a signal automaton is, an example will be given. Let one consider the language $\mathcal L$ of signals, over a binary alphabet $\$, which contains signals $\gamma$ such that:
* $A$ appears in singular intervals. That is, the set of times $\$ is discrete, and
* $A$ appears at least once during each interval of length one.
This language can be accepted by the automaton pictured nearby.
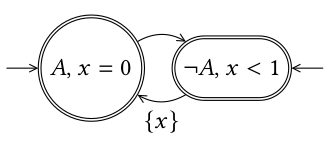
As for finite automaton, incoming arrows represents initial locations and double circle represents accepting locations. However, contrary to finite automata, letters occurs in locations and not in transition. This is because letters are emitted continuously and transitions are taken discretely. The symbol $x$ represents a clock. This clock allow to measure the time since the last time where $A$ was emitted. Thus $x=0$ ensures that $A$ is emitted discretely. And $1>x$ ensures that no more than a unit of time can pass without $A$ occurring.

Formal definition

Signal automaton

Formally, a signal automaton is a tuple $\mathcal A=\langle \Sigma,L,L_0,C,F,\alpha,\beta,E\rangle$ that consists of the following components:
* $\Sigma$ is a finite set called the alphabet or actions of $\mathcal A$.
* $L$ is a finite set. The elements of $L$ are called the locations or states of $\mathcal A$.
* $C$ is a finite set called the ''clocks of $\mathcal A$.
* $L_0\subseteq L$ is the set of start locations.
* $F\subseteq L$ is the set of accepting locations.
* $\alpha:L\to\Sigma$ which associates a letter to each location.
* $\beta:L\to\mathcal B(C)$ which associate a clock constraints to each location, and
* $E\subseteq L\times\mathcal P(C)\times L$ is a set of edges, called transitions of $\mathcal A$, where
** $\mathcal P(C)$ is the powerset of $C$.

An edge $(\ell,r,\ell')$ from $E$ is a transition from locations $\ell$ to $\ell'$ which reset the clocks of $r$.

Extended state

A pair with a location $\ell$ and a clock valuation $\nu$ is called either an ''extended state'' or a ''state''.

Note that the word state is thus ambiguous, since, depending on the author, it may means either a pair or an element of $L$. For the sake of the clarity, this article will use the term location for element of $L$ and the term extended location for pairs.

Here lies one of the biggest difference between signal-automata and finite automata. In a finite automaton, at some point of the execution, the state is entirely described by the number of letter read and by a finite number of possible values, which are actually called "states". That means that, given a state and a suffix of the word to read, the remaining of the run is totally determined. Thus, the word "finite" in the name "finite automata". However, as it is explained in the section "run" below, in order to resume clocks are used to determine which transitions can be taken. Thus, in order to know the state of the automaton, you must both now in which location you are, and the clock valuation.

Run

As for finite automata, a run is essentially a sequence of locations, such that there exists a transition between two locations. However, two differences must be emphasized. The letter is not determined by the transition but by the locations; this is due to the fact that the letters are emitted continuously while transitions are taken discretely. Some time elapses while in a location; the clock constraints labelling a location or its successor may constraint the time spent in a single location.

A ''run'' is a sequence of the form \xrightarrow nu_0\ell_0,I_0)\xrightarrow nu_1\ell_1,I_1)\dots satisfying some constraints. Before stating those constraints, some notations are introduced. The sequences are discrete but represents continuous events. A continuous version of the sequences $(\sigma_i)$, $(\nu_i)$, $(\ell_i)$ are now introduced. Let $i\ge0$ integral and $t\in I_i$, then
* let $\sigma'_t$ be equal to $\sigma_i$,
* let $\nu'_t$ be $\nu_i+t-\lceil I_i\rceil$ with $\lceil I_i\rceil$ being the lower bound of the interval $I_i$,
* let $\ell'_t=\ell_i$.

The constraints satisfied by run are, for each $i\ge0$ integral and $t\ge0$ real:
* $\ell_0\in L_0$,
* $(\ell_i,r_i,\ell_)\in E$,
* \nu_=(\nu_i+\mid I_i\mid) _i\rightarrow 0/math>,
* $\nu'_t\models\beta(\ell'_t)$.

The signal defined by this run is the function $\sigma'$ defined above. It is said that the run defined above is a run for the signal $\sigma'$.

The notion of accepting run is defined as in finite automata for finite words and as in Büchi automata for infinite words. That is, if $w$ is finite of length $n$, then the run is accepting if $\ell_\in F$. If the word is infinite, then the run is accepting if and only if there exists an infinite number of position $i$ such that $\ell_i\in F$.

Accepted signals and language

A signal $\gamma$ is said to be accepted by a signal automaton $\mathcal A$ if there exists a run of $\mathcal A$ on $\gamma$ accepting it. The set of signals accepted by $\mathcal A$ is called the language accepted by $\mathcal A$ and is denoted by $\mathcal$.

Deterministic signal automaton

As in the case of finite and Büchi automaton, a signal-automaton may be deterministic or non-deterministic. Intuitively, being deterministic as the same meaning in each of those case. It means that the set of start locations is a singleton, and that, given an extended state $s$, and a letter $a$, there is only one possible extended state which can be reached from $s$ by reading $a$. More precisely, either it is possible to stay in the location longer, or there is at most one possible successor location.

Formally, this can be defined as follows:
* $L_0$ is a singleton
* for each location $\ell\in L$, for each transition $(\ell,r,\ell')\in E$, the two following zones are disjoint:
** the zone defined by the clock constraint $\beta(\ell)$,
** the zone defined by the clock constraint $\beta(\ell')$ where the constraints on clocks of $r$ are removed,
* for each location transitions $(\ell,r',\ell')\in E$ and $(\ell,r'',\ell'')\in E$, the two following zones are disjoint:
** the zone defined by the clock constraint $\beta(\ell')$ where the constraints on clocks of $r'$ are removed,
** the zone defined by the clock constraint $\beta(\ell'')$ where the constraints on clocks of $r''$ are removed,

Simplified signal automata

Depending on the authors, the exact definition of signal automata may be slightly different. Two such definitions are now given.

Half-open intervals

In order to simplify the definition of a run, some authors requires that each interval of a run is right-closed and left-open. This restrict automata to accept only signals whose underlying partition satisfies the same property. However, it ensures that at each time $t\ge0$, $\lim_f(x)=f(t)$ for $f$ representing any of the function $\sigma'$, $\nu'$ or $\ell'$ introduced above.

Bipartite signal automaton

A bipartite signal automaton is a signal automaton in which the run alternates between open intervals and singular intervals (i.e. intervals which are singletons). It ensures that the graph underlying the automaton is a bipartite graph, and thus that the set of locations can be partitioned into $\$, the set of open locations and of singular locations. Since the first interval contains 0, it can not be an open location, it follows that $L_0\subseteq L^s$. In order to ensure that each singular location is indeed singular, for each location $\ell$, there must be a clock $x_\ell$ which is reset when entering $\ell$ and such that the clock constraint of $\ell$ contains $x=0$.

Any signal automaton can be transformed into an equivalent bipartite signal automaton. It suffices to replace each location $\ell$ by a pair of locations $(\ell^o,\ell^s)$ and introduce a new clock $x$, such that for each $\ell$, $x_=x$.

Nearby is pictured a bipartite automaton equivalent to the signal automaton from the example section. Rectangle states represents singular locations.

Synchronization of automata

The notion of product of finite automaton is extended to signal automaton. However, such a product is called a synchronization of automaton to emphasize the fact that the time should pass similarly in both automata considered. The main difference between synchronization and product is that, when two finite automata read the same word, they take transition simultaneously. This is not the case anymore for signal automata, since they can take transition at arbitrary time. Thus, the transition relation of a signal automaton may allow transition to be taken in one or two automata.

Let $\mathcal A^1=\langle \Sigma,L^1,L^1_0,C^1,F^1,\alpha^1,\beta^1,E^1\rangle$ and $\mathcal A^2=\langle \Sigma,L^2,L^2_0,C^2,F^2,\alpha^2,\beta^2,E^2\rangle$ two signal automata, their synchronization is the signal automaton $\mathcal A 1\otimes\mathcal A^2=\langle\Sigma,\,L^1_0\otimes L^2_0,C^1\cup C^2,F^1\otimes F^2,(\ell^1,\ell^2)\mapsto\alpha^1(\ell^1),(\ell^1,\ell^2)\mapsto\beta^1(\ell^1)\land\beta^2(\ell^2),E\rangle$, where $E$ contains the following transitions:
* $((\ell^1,\ell^2),r^1,(\ell^,\ell^2)$ for $(\ell^1,r,\ell^)\in E^1$, and similarly for $E^2$,
* $((\ell^1,\ell^2),r^1\cup r^2,(\ell^,\ell^)$ for $(\ell^1,r,\ell^)\in E^1$ and $(\ell^2,r,\ell^{\prime2})\in E^2$.

Difference with timed automata

Timed automata is another extension of finite automata, which adds a notion of time to words. We now state some of the main differences between timed automata and signal automata.

In timed automata, letters are emitted on the transitions and not in the locations. As explained above when comparing signal automata to finite automata, letters are emitted on transitions when the words are emitted discretely, as for words and timed-words while they are emitted on locations when letters are emitted continuously, as for signals.

In timed automata, guards are only checked on transitions. This simplifies the definition of deterministic automaton, since it means that the constraint must be satisfied before the clocks are restarted.

See also

*Timed automaton

Notes

Automata (computation)