Shape theory (mathematics)

Shape theory is a branch of topology that provides a more global view of the topological spaces than homotopy theory. The two coincide on compacta dominated homotopically by finite polyhedra. Shape theory associates with the Čech homology theory while homotopy theory associates with the singular homology theory.

Background

Shape theory was invented and published by D. E. Christie in 1944; it was reinvented, further developed and promoted by the Polish mathematician Karol Borsuk in 1968. Actually, the name ''shape theory'' was coined by Borsuk.

Warsaw circle

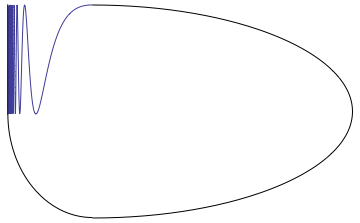
Borsuk lived and worked in Warsaw, hence the name of one of the fundamental examples of the area, the Warsaw circle.The Polish Circle and some of its unusual properties
. Math 205B-2012 Lecture Notes, University of California Riverside. Retrieved November 16, 2023. See also the accompanying diagram
Constructions on the Polish Circle
It is a compact subset of the plane produced by "closing up" a topologist's sine curve (also called a ''Warsaw sine curve'') with an arc. The homotopy groups of the Warsaw circle are all trivial, just like those of a point, and so any map between the Warsaw circle and a point induces a weak homotopy equivalence. However these two spaces are not homotopy equivalent. So by the Whitehead theorem, the Warsaw circle does not have the homotopy type of a CW complex.

Historical development

Borsuk's shape theory was generalized onto arbitrary (non-metric) compact spaces, and even onto general categories, by Włodzimierz Holsztyński in year 1968/1969, and published in Fund. Math. 70, 157–168, y. 1971 (see Jean-Marc Cordier, Tim Porter, (1989) below). This was done in a ''continuous style'', characteristic for the Čech homology rendered by Samuel Eilenberg and Norman Steenrod in their monograph ''Foundations of Algebraic Topology''. Due to the circumstance, Holsztyński's paper was hardly noticed, and instead a great popularity in the field was gained by a later paper by Sibe Mardešić and Jack Segal, Fund. Math. 72, 61–68, y.1971. Further developments are reflected by the references below, and by their contents.

For some purposes, like dynamical systems, more sophisticated invariants were developed under the name strong shape. Generalizations to noncommutative geometry, e.g. the shape theory for operator algebras have been found.

See also

* List of topologies

References

*
*
* Jean-Marc Cordier and Tim Porter, (1989), Shape Theory: Categorical Methods of Approximation, Mathematics and its Applications, Ellis Horwood. Reprinted Dover (2008)
* Aristide Deleanu and Peter John Hilton, On the categorical shape of a functor, Fundamenta Mathematicae 97 (1977) 157–176.
* Aristide Deleanu and Peter John Hilton, Borsuk's shape and Grothendieck categories of pro-objects, Mathematical Proceedings of the Cambridge Philosophical Society 79 (1976) 473–482.
* Sibe Mardešić and Jack Segal, Shapes of compacta and ANR-systems, Fundamenta Mathematicae 72 (1971) 41–59
* Karol Borsuk, Concerning homotopy properties of compacta, Fundamenta Mathematicae 62 (1968) 223–254
* Karol Borsuk, Theory of Shape, Monografie Matematyczne Tom 59, Warszawa 1975.
* D. A. Edwards and H. M. Hastings
Čech Theory: its Past, Present, and Future
Rocky Mountain Journal of Mathematics, Volume 10, Number 3, Summer 1980
* D. A. Edwards and H. M. Hastings, (1976)
Čech and Steenrod homotopy theories with applications to geometric topology
Lecture Notes in Mathematics 542, Springer-Verlag.
* Tim Porter, Čech homotopy I, II, Journal of the London Mathematical Society, 1, 6, 1973, pp. 429–436; 2, 6, 1973, pp. 667–675.
* J.T. Lisica and Sibe Mardešić, Coherent prohomotopy and strong shape theory, Glasnik Matematički 19(39) (1984) 335–399.
* Michael Batanin, Categorical strong shape theory, Cahiers Topologie Géom. Différentielle Catég. 38 (1997), no. 1, 3–66
numdam
* Marius Dădărlat, Shape theory and asymptotic morphisms for C*-algebras, Duke Mathematical Journal, 73(3):687–711, 1994.
* Marius Dădărlat and Terry A. Loring, Deformations of topological spaces predicted by E-theory, In Algebraic methods in operator theory, p. 316–327. Birkhäuser 1994.

{{Authority control

Topology
Homotopy theory