shape operator

In mathematics, the differential geometry of surfaces deals with the differential geometry of smooth surfaces with various additional structures, most often, a Riemannian metric.

Surfaces have been extensively studied from various perspectives: ''extrinsically'', relating to their embedding in Euclidean space and ''intrinsically'', reflecting their properties determined solely by the distance within the surface as measured along curves on the surface. One of the fundamental concepts investigated is the Gaussian curvature, first studied in depth by Carl Friedrich Gauss, who showed that curvature was an intrinsic property of a surface, independent of its isometric embedding in Euclidean space.

Surfaces naturally arise as graphs of functions of a pair of variables, and sometimes appear in parametric form or as loci associated to space curves. An important role in their study has been played by Lie groups (in the spirit of the Erlangen program), namely the symmetry groups of the Euclidean plane, the sphere and the hyperbolic plane. These Lie groups can be used to describe surfaces of constant Gaussian curvature; they also provide an essential ingredient in the modern approach to intrinsic differential geometry through connections. On the other hand, extrinsic properties relying on an embedding of a surface in Euclidean space have also been extensively studied. This is well illustrated by the non-linear Euler–Lagrange equations in the calculus of variations: although Euler developed the one variable equations to understand geodesics, defined independently of an embedding, one of Lagrange's main applications of the two variable equations was to minimal surfaces, a concept that can only be defined in terms of an embedding.

History

The volumes of certain quadric surfaces of revolution were calculated by Archimedes. The development of calculus in the seventeenth century provided a more systematic way of computing them. Curvature of general surfaces was first studied by Euler. In 1760 he proved a formula for the curvature of a plane section of a surface and in 1771 he considered surfaces represented in a parametric form. Monge laid down the foundations of their theory in his classical memoir ''L'application de l'analyse à la géometrie'' which appeared in 1795. The defining contribution to the theory of surfaces was made by Gauss in two remarkable papers written in 1825 and 1827. This marked a new departure from tradition because for the first time Gauss considered the ''intrinsic'' geometry of a surface, the properties which are determined only by the geodesic distances between points on the surface independently of the particular way in which the surface is located in the ambient Euclidean space. The crowning result, the Theorema Egregium of Gauss, established that the Gaussian curvature is an intrinsic invariant, i.e. invariant under local isometries. This point of view was extended to higher-dimensional spaces by Riemann and led to what is known today as Riemannian geometry. The nineteenth century was the golden age for the theory of surfaces, from both the topological and the differential-geometric point of view, with most leading geometers devoting themselves to their study. Darboux collected many results in his four-volume treatise ''Théorie des surfaces'' (1887–1896).

Overview

It is intuitively quite familiar to say that the leaf of a plant, the surface of a glass, or the shape of a face, are curved in certain ways, and that all of these shapes, even after ignoring any distinguishing markings, have certain geometric features which distinguish one from another. The differential geometry of surfaces is concerned with a mathematical understanding of such phenomena. The study of this field, which was initiated in its modern form in the 1700s, has led to the development of higher-dimensional and abstract geometry, such as Riemannian geometry and general relativity.

The essential mathematical object is that of a regular surface. Although conventions vary in their precise definition, these form a general class of subsets of three-dimensional Euclidean space () which capture part of the familiar notion of "surface." By analyzing the class of curves which lie on such a surface, and the degree to which the surfaces force them to curve in , one can associate to each point of the surface two numbers, called the ''principal curvatures''. Their average is called the ''mean curvature'' of the surface, and their product is called the ''Gaussian curvature''.

There are many classic examples of regular surfaces, including:
* familiar examples such as planes, cylinders, and spheres
*minimal surfaces, which are defined by the property that their mean curvature is zero at every point. The best-known examples are catenoids and helicoids, although many more have been discovered. Minimal surfaces can also be defined by properties to do with surface area, with the consequence that they provide a mathematical model for the shape of soap films when stretched across a wire frame
*ruled surfaces, which are surfaces that have at least one straight line running through every point; examples include the cylinder and the hyperboloid of one sheet.

A surprising result of Carl Friedrich Gauss, known as the '' Theorema Egregium'', showed that the Gaussian curvature of a surface, which by its definition has to do with how curves on the surface change directions in three dimensional space, can actually be measured by the lengths of curves lying on the surfaces together with the angles made when two curves on the surface intersect. Terminologically, this says that the Gaussian curvature can be calculated from the ''first fundamental form'' (also called metric tensor) of the surface. The '' second fundamental form'', by contrast, is an object which encodes how lengths and angles of curves on the surface are distorted when the curves are pushed off of the surface.

Despite measuring different aspects of length and angle, the first and second fundamental forms are not independent from one another, and they satisfy certain constraints called the ''Gauss–Codazzi equations''. A major theorem, often called the fundamental theorem of the differential geometry of surfaces, asserts that whenever two objects satisfy the Gauss-Codazzi constraints, they will arise as the first and second fundamental forms of a regular surface.

Using the first fundamental form, it is possible to define new objects on a regular surface. ''Geodesics'' are curves on the surface which satisfy a certain second-order ordinary differential equation which is specified by the first fundamental form. They are very directly connected to the study of lengths of curves; a geodesic of sufficiently short length will always be the curve of shortest length on the surface which connects its two endpoints. Thus, geodesics are fundamental to the optimization problem of determining the shortest path between two given points on a regular surface.

One can also define ''parallel transport'' along any given curve, which gives a prescription for how to deform a tangent vector to the surface at one point of the curve to tangent vectors at all other points of the curve. The prescription is determined by a first-order ordinary differential equation which is specified by the first fundamental form.

The above concepts are essentially all to do with multivariable calculus. The ''Gauss–Bonnet theorem'' is a more global result, which relates the Gaussian curvature of a surface together with its topological type. It asserts that the average value of the Gaussian curvature is completely determined by the Euler characteristic of the surface together with its surface area.

Any regular surface is an example both of a ''Riemannian manifold'' and ''Riemann surface''. Essentially all of the theory of regular surfaces as discussed here has a generalization in the theory of Riemannian manifolds and their submanifolds.

Regular surfaces in Euclidean space

Definition

It is intuitively clear that a sphere is smooth, while a cone or a pyramid, due to their vertex or edges, are not. The notion of a "regular surface" is a formalization of the notion of a smooth surface. The definition utilizes the local representation of a surface via maps between Euclidean spaces. There is a standard notion of smoothness for such maps; a map between two open subsets of Euclidean space is smooth if its partial derivatives of every order exist at every point of the domain.

A regular surface in Euclidean space is a subset of such that every point of admits any of the following three concepts: ''local parametrizations'', ''Monge patches'', or ''implicit functions''.
The following table gives definitions of such objects; Monge patches is perhaps the most visually intuitive, as it essentially says that a regular surface is a subset of which is locally the graph of a smooth function (whether over a region in the plane, the plane, or the plane).

The homeomorphisms appearing in the first definition are known as local parametrizations or local coordinate systems or local charts on . The equivalence of the first two definitions asserts that, around any point on a regular surface, there always exist local parametrizations of the form , , or , known as Monge patches. Functions as in the third definition are called local defining functions. The equivalence of all three definitions follows from the implicit function theorem.

Given any two local parametrizations and of a regular surface, the composition is necessarily smooth as a map between open subsets of . This shows that any regular surface naturally has the structure of a smooth manifold, with a smooth atlas being given by the inverses of local parametrizations.

In the classical theory of differential geometry, surfaces are usually studied only in the regular case. It is, however, also common to study non-regular surfaces, in which the two partial derivatives and of a local parametrization may fail to be linearly independent. In this case, may have singularities such as cuspidal edges. Such surfaces are typically studied in singularity theory. Other weakened forms of regular surfaces occur in computer-aided design, where a surface is broken apart into disjoint pieces, with the derivatives of local parametrizations failing to even be continuous along the boundaries.

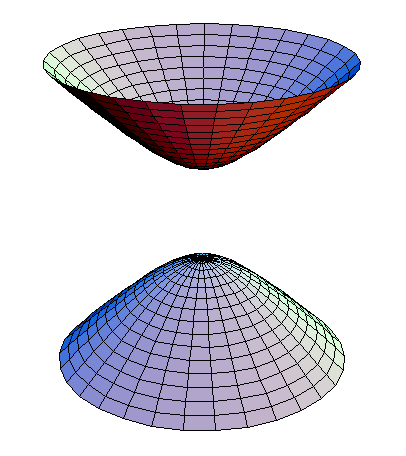
Simple examples. A simple example of a regular surface is given by the 2-sphere ; this surface can be covered by six Monge patches (two of each of the three types given above), taking . It can also be covered by two local parametrizations, using stereographic projection. The set is a torus of revolution with radii and . It is a regular surface; local parametrizations can be given of the form
:$f(s,t)=\big((R \cos s +r)\cos t, (R \cos s +r) \sin t, R\sin s\big).$
The hyperboloid on two sheets is a regular surface; it can be covered by two Monge patches, with . The helicoid appears in the theory of minimal surfaces. It is covered by a single local parametrization, .

Tangent vectors and normal vectors

Let be a regular surface in , and let be an element of . Using any of the above definitions, one can single out certain vectors in as being tangent to at , and certain vectors in as being orthogonal to at .

One sees that the ''tangent space'' or ''tangent plane'' to at , which is defined to consist of all tangent vectors to at , is a two-dimensional linear subspace of ; it is often denoted by . The ''normal space'' to at , which is defined to consist of all normal vectors to at , is a one-dimensional linear subspace of which is orthogonal to the tangent space . As such, at each point of , there are two normal vectors of unit length (unit normal vectors). The unit normal vectors at can be given in terms of local parametrizations, Monge patches, or local defining functions, via the formulas
:$\pm\left.\frac\_,\qquad \pm\left.\frac\_,\qquad\text\qquad\pm\frac,$
following the same notations as in the previous definitions.

It is also useful to note an "intrinsic" definition of tangent vectors, which is typical of the generalization of regular surface theory to the setting of smooth manifolds. It defines the tangent space as an abstract two-dimensional real vector space, rather than as a linear subspace of . In this definition, one says that a tangent vector to at is an assignment, to each local parametrization with , of two numbers and , such that for any other local parametrization with (and with corresponding numbers and ), one has
:$\beginX^1\\ X^2\end=A_\begin(X')^1\\ (X')^2\end,$
where is the Jacobian matrix of the mapping , evaluated at the point . The collection of tangent vectors to at naturally has the structure of a two-dimensional vector space. A tangent vector in this sense corresponds to a tangent vector in the previous sense by considering the vector
:$X^1\frac+X^2\frac.$
in . The Jacobian condition on and ensures, by the chain rule, that this vector does not depend on .

For smooth functions on a surface, vector fields (i.e. tangent vector fields) have an important interpretation as first order operators or derivations. Let $S$ be a regular surface, $U$ an open subset of the plane and $f:U\rightarrow S$ a coordinate chart. If $V=f(U)$, the space $C^\infty(U)$ can be identified with $C^\infty(V)$. Similarly $f$ identifies vector fields on $U$ with vector fields on $V$. Taking standard variables and , a vector field has the form $X= a\partial_u + b\partial_v$, with and smooth functions. If $X$ is a vector field and $g$ is a smooth function, then $Xg$ is also a smooth function. The first order differential operator $X$ is a ''derivation'', i.e. it satisfies the Leibniz rule $X(gh)= (Xg) h + g (Xh).$

For vector fields and it is simple to check that the operator ,YXY-YX is a derivation corresponding to a vector field. It is called the Lie bracket ,Y/math>. It is skew-symmetric ,Y- ,X/math> and satisfies the Jacobi identity:

: X,YZ] + Y,ZX] + Z,XY]=0.

In summary, vector fields on $U$ or $V$ form a Lie algebra under the Lie bracket.

First and second fundamental forms, the shape operator, and the curvature

Let be a regular surface in . Given a local parametrization and a unit normal vector field to , one defines the following objects as real-valued or matrix-valued functions on . The first fundamental form depends only on , and not on . The fourth column records the way in which these functions depend on , by relating the functions etc., arising for a different choice of local parametrization, , to those arising for . Here denotes the Jacobian matrix of . The key relation in establishing the formulas of the fourth column is then
:$\begin\frac\\ \frac\end=A\begin\frac\\ \frac\end,$
as follows by the chain rule.

By a direct calculation with the matrix defining the shape operator, it can be checked that the Gaussian curvature is the determinant of the shape operator, the mean curvature is half of the trace of the shape operator, and the principal curvatures are the eigenvalues of the shape operator; moreover the Gaussian curvature is the product of the principal curvatures and the mean curvature is their sum. These observations can also be formulated as definitions of these objects. These observations also make clear that the last three rows of the fourth column follow immediately from the previous row, as similar matrices have identical determinant, trace, and eigenvalues. It is fundamental to note , , and are all necessarily positive. This ensures that the matrix inverse in the definition of the shape operator is well-defined, and that the principal curvatures are real numbers.

Note also that a negation of the choice of unit normal vector field will negate the second fundamental form, the shape operator, the mean curvature, and the principal curvatures, but will leave the Gaussian curvature unchanged. In summary, this has shown that, given a regular surface , the Gaussian curvature of can be regarded as a real-valued function on ; relative to a choice of unit normal vector field on all of , the two principal curvatures and the mean curvature are also real-valued functions on .

Geometrically, the first and second fundamental forms can be viewed as giving information on how moves around in as moves around in . In particular, the first fundamental form encodes how quickly moves, while the second fundamental form encodes the extent to which its motion is in the direction of the normal vector . In other words, the second fundamental form at a point encodes the length of the orthogonal projection from to the tangent plane to at ; in particular it gives the quadratic function which best approximates this length. This thinking can be made precise by the formulas
:$\begin \lim_\frac &= 0\\ \lim_\frac &= 0, \end$
as follows directly from the definitions of the fundamental forms and Taylor's theorem in two dimensions. The principal curvatures can be viewed in the following way. At a given point of , consider the collection of all planes which contain the orthogonal line to . Each such plane has a curve of intersection with , which can be regarded as a plane curve inside of the plane itself. The two principal curvatures at are the maximum and minimum possible values of the curvature of this plane curve at , as the plane under consideration rotates around the normal line.

The following summarizes the calculation of the above quantities relative to a Monge patch . Here and denote the two partial derivatives of , with analogous notation for the second partial derivatives. The second fundamental form and all subsequent quantities are calculated relative to the given choice of unit normal vector field.

Christoffel symbols, Gauss–Codazzi equations, and the Theorema Egregium

Let be a regular surface in . The Christoffel symbols assign, to each local parametrization , eight functions on , defined by
:$\begin\Gamma_^1&\Gamma_^1&\Gamma_^1&\Gamma_^1\\ \Gamma_^2&\Gamma_^2&\Gamma_^2&\Gamma_^2\end=\beginE&F\\ F&G\end^\begin\frac\frac&\frac\frac&\frac\frac &\frac-\frac\frac\\ \frac-\frac\frac&\frac\frac&\frac\frac&\frac\frac\end.$
They can also be defined by the following formulas, in which is a unit normal vector field along and are the corresponding components of the second fundamental form:
:$\begin \frac&=\Gamma_^1\frac+\Gamma_^2\frac+Ln\\ \frac&=\Gamma_^1\frac+\Gamma_^2\frac+Mn\\ \frac&=\Gamma_^1\frac+\Gamma_^2\frac+Nn. \end$
The key to this definition is that , , and form a basis of at each point, relative to which each of the three equations uniquely specifies the Christoffel symbols as coordinates of the second partial derivatives of . The choice of unit normal has no effect on the Christoffel symbols, since if is exchanged for its negation, then the components of the second fundamental form are also negated, and so the signs of are left unchanged.

The second definition shows, in the context of local parametrizations, that the Christoffel symbols are geometrically natural. Although the formulas in the first definition appear less natural, they have the importance of showing that the Christoffel symbols can be calculated from the first fundamental form, which is not immediately apparent from the second definition. The equivalence of the definitions can be checked by directly substituting the first definition into the second, and using the definitions of .

The Codazzi equations assert that
:$\begin \frac-\frac&=L\Gamma_^1 + M(\Gamma_^2-\Gamma_^1) - N\Gamma_^2\\ \frac-\frac&=L\Gamma_^1 + M(\Gamma_^2-\Gamma_^1) - N\Gamma_^2. \end$
These equations can be directly derived from the second definition of Christoffel symbols given above; for instance, the first Codazzi equation is obtained by differentiating the first equation with respect to , the second equation with respect to , subtracting the two, and taking the dot product with . The Gauss equation asserts that
:$\begin KE&=\frac-\frac+\Gamma_^2\Gamma_^1+\Gamma_^2\Gamma_^2-\Gamma_^2\Gamma_^1-\Gamma_^2\Gamma_^2\\ KF&=\frac-\frac+\Gamma_^2\Gamma_^1-\Gamma_^2\Gamma_^1\\ KG&=\frac-\frac+\Gamma_^1\Gamma_^1+\Gamma_^1\Gamma_^2-\Gamma_^1\Gamma_^1-\Gamma_^1\Gamma_^2 \end$
These can be similarly derived as the Codazzi equations, with one using the Weingarten equations instead of taking the dot product with . Although these are written as three separate equations, they are identical when the definitions of the Christoffel symbols, in terms of the first fundamental form, are substituted in. There are many ways to write the resulting expression, one of them derived in 1852 by Brioschi using a skillful use of determinants:
:$K = \frac\det\begin-\frac + \frac - \frac & \frac & \frac - \frac\\ \frac - \frac & E & F \\ \frac& F & G\end-\frac\det\begin 0 & \frac & \frac\\ \frac & E & F \\ \frac& F & G\end.$
When the Christoffel symbols are considered as being defined by the first fundamental form, the Gauss and Codazzi equations represent certain constraints between the first and second fundamental forms. The Gauss equation is particularly noteworthy, as it shows that the Gaussian curvature can be computed directly from the first fundamental form, without the need for any other information; equivalently, this says that can actually be written as a function of , even though the individual components cannot. This is known as the theorema egregium, and was a major discovery of Carl Friedrich Gauss. It is particularly striking when one recalls the geometric definition of the Gaussian curvature of as being defined by the maximum and minimum radii of osculating circles; they seem to be fundamentally defined by the geometry of how bends within . Nevertheless, the theorem shows that their product can be determined from the "intrinsic" geometry of , having only to do with the lengths of curves along and the angles formed at their intersections. As said by Marcel Berger:

The Gauss-Codazzi equations can also be succinctly expressed and derived in the language of connection forms due to Élie Cartan. In the language of tensor calculus, making use of natural metrics and connections on tensor bundles, the Gauss equation can be written as and the two Codazzi equations can be written as and ; the complicated expressions to do with Christoffel symbols and the first fundamental form are completely absorbed into the definitions of the covariant tensor derivative and the scalar curvature . Pierre Bonnet proved that two quadratic forms satisfying the Gauss-Codazzi equations always uniquely determine an embedded surface locally. For this reason the Gauss-Codazzi equations are often called the fundamental equations for embedded surfaces, precisely identifying where the intrinsic and extrinsic curvatures come from. They admit generalizations to surfaces embedded in more general Riemannian manifolds.

Isometries

A diffeomorphism $\varphi$ between open sets $U$ and $V$ in a regular surface $S$ is said to be an isometry if it preserves the metric, i.e. the first fundamental form. Thus for every point $p$ in $U$ and tangent vectors $w_1,\,\, w_2$ at $p$, there are equalities

:$E(p) w_1\cdot w_1 + 2F(p) w_1\cdot w_2 + G(p) w_2\cdot w_2= E(\varphi(p)) \varphi^\prime(w_1)\cdot \varphi^\prime(w_1) +2F(\varphi(p)) \varphi^\prime(w_1)\cdot \varphi^\prime(w_2) + G (\varphi(p)) \varphi^\prime(w_1)\cdot \varphi^\prime(w_2).$

In terms of the inner product coming from the first fundamental form, this can be rewritten as

:$(w_1,w_2)_p=(\varphi^\prime(w_1),\varphi^\prime(w_2))_$.

On the other hand, the length of a parametrized curve $\gamma(t)=(x(t),y(t))$ can be calculated as

:$L(\gamma)=\int_a^b \sqrt \, dt$

and, if the curve lies in $U$, the rules for change of variables show that

:$L(\varphi\circ \gamma) = L(\gamma).$

Conversely if $\varphi$ preserves the lengths of all parametrized in curves then $\varphi$ is an isometry. Indeed, for suitable choices of $\gamma$, the tangent vectors $\dot$ and $\dot$ give arbitrary tangent vectors $w_1$ and $w_2$. The equalities must hold for all choice of tangent vectors $w_1$ and $w_2$ as well as $\varphi^\prime(w_1)$ and $\varphi^\prime(w_2)$, so that $(\varphi^\prime(w_1),\varphi^\prime(w_2))_ = (w_1,w_1)_p$.

A simple example of an isometry is provided by two parametrizations $f_1$ and $f_2$ of an open set $U$ into regular surfaces $S_1$ and $S_2$. If $E_1=E_2$, $F_1=F_2$ and $G_1=G_2$, then $\varphi=f_2\circ f_1^$ is an isometry of $f_1(U)$ onto $f_2(U)$.

The cylinder and the plane give examples of surfaces that are locally isometric but which cannot be extended to an isometry for topological reasons. As another example, the catenoid and helicoid are locally isometric.

Covariant derivatives

A tangential vector field on assigns, to each in , a tangent vector to at . According to the "intrinsic" definition of tangent vectors given above, a tangential vector field then assigns, to each local parametrization , two real-valued functions and on , so that
:$X_p=X^1\big(f^(p)\big)\frac\Big, _+X^2\big(f^(p)\big)\frac\Big, _$
for each in . One says that is smooth if the functions and are smooth, for any choice of . According to the other definitions of tangent vectors given above, one may also regard a tangential vector field on as a map such that is contained in the tangent space for each in . As is common in the more general situation of smooth manifolds, tangential vector fields can also be defined as certain differential operators on the space of smooth functions on .

The covariant derivatives (also called "tangential derivatives") of Tullio Levi-Civita and Gregorio Ricci-Curbastro provide a means of differentiating smooth tangential vector fields. Given a tangential vector field and a tangent vector to at , the covariant derivative is a certain tangent vector to at . Consequently, if and are both tangential vector fields, then can also be regarded as a tangential vector field; iteratively, if , , and are tangential vector fields, the one may compute , which will be another tangential vector field. There are a few ways to define the covariant derivative; the first below uses the Christoffel symbols and the "intrinsic" definition of tangent vectors, and the second is more manifestly geometric.

Given a tangential vector field and a tangent vector to at , one defines to be the tangent vector to which assigns to a local parametrization the two numbers
:$(\nabla_YX)^k=D_X^k\Big, _+\sum_^2\sum_^2\big(\Gamma_^kX^j\big)\Big, _Y^i,\qquad(k=1,2)$
where is the directional derivative.Do Carmo, page 242 This is often abbreviated in the less cumbersome form , making use of Einstein notation and with the locations of function evaluation being implicitly understood. This follows a standard prescription in Riemannian geometry for obtaining a connection from a Riemannian metric. It is a fundamental fact that the vector
:$(\nabla_YX)^1\frac+(\nabla_YX)^2\frac$
in is independent of the choice of local parametization , although this is rather tedious to check.

One can also define the covariant derivative by the following geometric approach, which does not make use of Christoffel symbols or local parametrizations. Let be a vector field on , viewed as a function . Given any curve , one may consider the composition . As a map between Euclidean spaces, it can be differentiated at any input value to get an element of . The orthogonal projection of this vector onto defines the covariant derivative . Although this is a very geometrically clean definition, it is necessary to show that the result only depends on and , and not on and ; local parametrizations can be used for this small technical argument.

It is not immediately apparent from the second definition that covariant differentiation depends only on the first fundamental form of ; however, this is immediate from the first definition, since the Christoffel symbols can be defined directly from the first fundamental form. It is straightforward to check that the two definitions are equivalent. The key is that when one regards as a -valued function, its differentiation along a curve results in second partial derivatives ; the Christoffel symbols enter with orthogonal projection to the tangent space, due to the formulation of the Christoffel symbols as the tangential components of the second derivatives of relative to the basis , , . This is discussed in the above section.

The right-hand side of the three Gauss equations can be expressed using covariant differentiation. For instance, the right-hand side
:$\frac-\frac+\Gamma_^2\Gamma_^1+\Gamma_^2\Gamma_^2-\Gamma_^2\Gamma_^1-\Gamma_^2\Gamma_^2$
can be recognized as the second coordinate of
:$\nabla_\nabla_\frac-\nabla_\nabla_\frac$
relative to the basis , , as can be directly verified using the definition of covariant differentiation by Christoffel symbols. In the language of Riemannian geometry, this observation can also be phrased as saying that the right-hand sides of the Gauss equations are various components of the Ricci curvature of the Levi-Civita connection of the first fundamental form, when interpreted as a Riemannian metric.

Examples

Surfaces of revolution

A surface of revolution is obtained by rotating a curve in the -plane about the -axis. Such surfaces include spheres, cylinders, cones, tori, and the catenoid. The general ellipsoids, hyperboloids, and paraboloids are not. Suppose that the curve is parametrized by
:$x= c_1(s),\,\, z=c_2(s)$
with drawn from an interval . If is never zero, if and are never both equal to zero, and if and are both smooth, then the corresponding surface of revolution
:$S=\Big\$
will be a regular surface in . A local parametrization is given by
:$f(s,t)=\big(c_1(s)\cos t, c_1(s)\sin t,c_2(s)\big).$
Relative to this parametrization, the geometric data is:

In the special case that the original curve is parametrized by arclength, i.e. , one can differentiate to find . On substitution into the Gaussian curvature, one has the simplified
:$K=-\frac\qquad\text\qquad H=c_1'(s)c_2''(s)-c_2'(s)c_1''(s)+\frac.$
The simplicity of this formula makes it particularly easy to study the class of rotationally symmetric surfaces with constant Gaussian curvature. By reduction to the alternative case that , one can study the rotationally symmetric minimal surfaces, with the result that any such surface is part of a plane or a scaled catenoid.

Each constant- curve on can be parametrized as a geodesic; a constant- curve on can be parametrized as a geodesic if and only if is equal to zero. Generally, geodesics on are governed by Clairaut's relation.

Quadric surfaces

Consider the quadric surface defined by
:$+ +=1.$
This surface admits a parametrization
:$x=\sqrt,\,\, y=\sqrt, \,\, z=\sqrt.$
The Gaussian curvature and mean curvature are given by
:$K= ,\,\,K_m=-(u+v)\sqrt.$

Ruled surfaces

A ruled surface is one which can be generated by the motion of a straight line in . Choosing a ''directrix'' on the surface, i.e. a smooth unit speed curve orthogonal to the straight lines, and then choosing to be unit vectors along the curve in the direction of the lines, the velocity vector and satisfy
:$u\cdot v=0, \,\,\, u\, =1,\,\,\, v\, =1.$
The surface consists of points
:$c(t) + s\cdot u(t)$
as and vary.

Then, if
:$a=\, u_t\, , \,\, b=u_t\cdot v, \,\, \alpha=-\frac, \,\, \beta=\frac,$
the Gaussian and mean curvature are given by
:$K=- ,\,\, K_m=-.$

The Gaussian curvature of the ruled surface vanishes if and only if and are proportional, This condition is equivalent to the surface being the envelope of the planes along the curve containing the tangent vector and the orthogonal vector , i.e. to the surface being developable along the curve. More generally a surface in has vanishing Gaussian curvature near a point if and only if it is developable near that point. (An equivalent condition is given below in terms of the metric.)

Minimal surfaces

In 1760 Lagrange involving integrals in one variable to two variables. He had in mind the following problem:

Such a surface is called a minimal surface.

In 1776 Jean Baptiste Meusnier showed that the differential equation derived by Lagrange was equivalent to the vanishing of the mean curvature of the surface:

Minimal surfaces have a simple interpretation in real life: they are the shape a soap film will assume if a wire frame shaped like the curve is dipped into a soap solution and then carefully lifted out. The question as to whether a minimal surface with given boundary exists is called Plateau's problem after the Belgian physicist Joseph Plateau who carried out experiments on soap films in the mid-nineteenth century. In 1930 Jesse Douglas and Tibor Radó gave an affirmative answer to Plateau's problem (Douglas was awarded one of the first Fields medals for this work in 1936).

Many explicit examples of minimal surface are known explicitly, such as the catenoid, the helicoid, the Scherk surface and the Enneper surface. There has been extensive research in this area, summarised in . In particular a result of Osserman shows that if a minimal surface is non-planar, then its image under the Gauss map is dense in .

Surfaces of constant Gaussian curvature

If a surface has constant Gaussian curvature, it is called a surface of constant curvature.

*The unit sphere in has constant Gaussian curvature +1.
*The Euclidean plane and the cylinder both have constant Gaussian curvature 0.
*A unit pseudosphere has constant Gaussian curvature -1 (apart from its equator, that is singular). Pseudosphere can be obtained by rotating a tractrix around its asymptote. In 1868 Eugenio Beltrami showed that the geometry of the pseudosphere was directly related to that of the more abstract hyperbolic plane, discovered independently by Lobachevsky (1830) and Bolyai (1832). Already in 1840, F. Minding, a student of Gauss, had obtained trigonometric formulas for the pseudosphere identical to those for the hyperbolic plane. The intrinsic geometry of this surface is now better understood in terms of the Poincaré metric on the upper half plane or the unit disc, and has been described by other models such as the Klein model or the hyperboloid model, obtained by considering the two-sheeted hyperboloid in three-dimensional Minkowski space, where .

The sphere, the plane and the hyperbolic plane have transitive Lie group of symmetries. This group theoretic fact has far-reaching consequences, all the more remarkable because of the central role these special surfaces play in the geometry of surfaces, due to Poincaré's uniformization theorem (see below).

Other examples of surfaces with Gaussian curvature 0 include cones, tangent developables, and more generally any developable surface.

Local metric structure

For any surface embedded in Euclidean space of dimension 3 or higher, it is possible to measure the length of a curve on the surface, the angle between two curves and the area of a region on the surface. This structure is encoded infinitesimally in a Riemannian metric on the surface through ''line elements'' and ''area elements''. Classically in the nineteenth and early twentieth centuries only surfaces embedded in were considered and the metric was given as a 2×2 positive definite matrix varying smoothly from point to point in a local parametrization of the surface. The idea of local parametrization and change of coordinate was later formalized through the current abstract notion of a manifold, a topological space where the smooth structure is given by local charts on the manifold, exactly as the planet Earth is mapped by atlases today. Changes of coordinates between different charts of the same region are required to be smooth. Just as contour lines on real-life maps encode changes in elevation, taking into account local distortions of the Earth's surface to calculate true distances, so the Riemannian metric describes distances and areas "in the small" in each local chart. In each local chart a Riemannian metric is given by smoothly assigning a 2×2 positive definite matrix to each point; when a different chart is taken, the matrix is transformed according to the Jacobian matrix of the coordinate change. The manifold then has the structure of a 2-dimensional Riemannian manifold.

Shape operator

The differential of the Gauss map can be used to define a type of extrinsic curvature, known as the shape operator or Weingarten map. This operator first appeared implicitly in the work of Wilhelm Blaschke and later explicitly in a treatise by Burali-Forti and Burgati. Since at each point of the surface, the tangent space is an inner product space, the shape operator can be defined as a linear operator on this space by the formula
:$(S_x v, w) =(dn(v), w)$
for tangent vectors , (the inner product makes sense because and both lie in ). The right hand side is symmetric in and , so the shape operator is self-adjoint on the tangent space. The eigenvalues of are just the principal curvatures and at . In particular the determinant of the shape operator at a point is the Gaussian curvature, but it also contains other information, since the mean curvature is half the trace of the shape operator. The mean curvature is an extrinsic invariant. In intrinsic geometry, a cylinder is developable, meaning that every piece of it is intrinsically indistinguishable from a piece of a plane since its Gauss curvature vanishes identically. Its mean curvature is not zero, though; hence extrinsically it is different from a plane.

Equivalently, the shape operator can be defined as a linear operator on tangent spaces, $S_p:T_pM\rightarrow T_pM$. If ''n'' is a unit normal field to ''M'' and ''v'' is a tangent vector then
:$S(v)=\pm \nabla_n$
(there is no standard agreement whether to use + or − in the definition).

In general, the eigenvectors and eigenvalues of the shape operator at each point determine the directions in which the surface bends at each point. The eigenvalues correspond to the principal curvatures of the surface and the eigenvectors are the corresponding principal directions. The principal directions specify the directions that a curve embedded in the surface must travel to have maximum and minimum curvature, these being given by the principal curvatures.

Geodesic curves on a surface

Curves on a surface which minimize length between the endpoints are called geodesics; they are the shape that an elastic band stretched between the two points would take. Mathematically they are described using ordinary differential equations and the calculus of variations. The differential geometry of surfaces revolves around the study of geodesics. It is still an open question whether every Riemannian metric on a 2-dimensional local chart arises from an embedding in 3-dimensional Euclidean space: the theory of geodesics has been used to show this is true in the important case when the components of the metric are analytic.

Geodesics

Given a piecewise smooth path $c(t)=(x(t),y(t))$ in the chart for $t$ in ,b/math>, its ''length'' is defined by
:$L(c) = \int_a^b (E\dot^2 + 2F \dot\dot + G \dot^2)^\, dt$
and ''energy'' by
:$E(c) = \int_a^b (E\dot^2 + 2F \dot\dot + G \dot^2)\, dt.$

The length is independent of the parametrization of a path. By the Euler–Lagrange equations, if is a path minimising length, ''parametrized by arclength'', it must satisfy the Euler equations
:$\ddot + \Gamma_^1 \dot^2 + 2\Gamma_^1 \dot\dot+ \Gamma_^1\dot^2 =0$
:$\ddot+ \Gamma_^2 \dot^2 + 2\Gamma_^2 \dot\dot+ \Gamma_^2 \dot^2 =0$
where the Christoffel symbols are given by
:$\Gamma_^k = \tfrac12 g^(\partial_j g_ + \partial_i g_ - \partial_m g_)$
where , , and is the inverse matrix to . A path satisfying the Euler equations is called a geodesic. By the Cauchy–Schwarz inequality a path minimising energy is just a geodesic parametrised by arc length; and, for any geodesic, the parameter is proportional to arclength.

Geodesic curvature

The geodesic curvature at a point of a curve , parametrised by arc length, on an oriented surface is defined to be
:$k_g= \ddot(t)\cdot \mathbf(t).$
where is the "principal" unit normal to the curve in the surface, constructed by rotating the unit tangent vector through an angle of +90°.

*The geodesic curvature at a point is an intrinsic invariant depending only on the metric near the point.
*A unit speed curve on a surface is a geodesic if and only if its geodesic curvature vanishes at all points on the curve.
*A unit speed curve in an embedded surface is a geodesic if and only if its acceleration vector is normal to the surface.

The geodesic curvature measures in a precise way how far a curve on the surface is from being a geodesic.

Orthogonal coordinates

When throughout a coordinate chart, such as with the geodesic polar coordinates discussed below, the images of lines parallel to the - and -axes are orthogonal and provide orthogonal coordinates. If , then the Gaussian curvature is given by
: K=- \left partial_x\left(\frac\right) +\partial_y\left(\frac\right)\right

If in addition , so that , then the angle at the intersection between geodesic and the line = constant is given by the equation
:$\tan \varphi = H\cdot \frac.$
The derivative of is given by a classical derivative formula of Gauss:
:$\dot = -H_x \cdot \dot.$

Geodesic polar coordinates

Once a metric is given on a surface and a base point is fixed, there is a unique geodesic connecting the base point to each sufficiently nearby point. The direction of the geodesic at the base point and the distance uniquely determine the other endpoint. These two bits of data, a direction and a magnitude, thus determine a tangent vector at the base point. The map from tangent vectors to endpoints smoothly sweeps out a neighbourhood of the base point and defines what is called the '' exponential map'', defining a local coordinate chart at that base point. The neighbourhood swept out has similar properties to balls in Euclidean space, namely any two points in it are joined by a unique geodesic. This property is called "geodesic convexity" and the coordinates are called ''normal coordinates''. The explicit calculation of normal coordinates can be accomplished by considering the differential equation satisfied by geodesics. The convexity properties are consequences of Gauss's lemma and its generalisations. Roughly speaking this lemma states that geodesics starting at the base point must cut the spheres of fixed radius centred on the base point at right angles. Geodesic polar coordinates are obtained by combining the exponential map with polar coordinates on tangent vectors at the base point. The Gaussian curvature of the surface is then given by the second order deviation of the metric at the point from the Euclidean metric. In particular the Gaussian curvature is an invariant of the metric, Gauss's celebrated '' Theorema Egregium''. A convenient way to understand the curvature comes from an ordinary differential equation, first considered by Gauss and later generalized by Jacobi, arising from the change of normal coordinates about two different points. The Gauss–Jacobi equation provides another way of computing the Gaussian curvature. Geometrically it explains what happens to geodesics from a fixed base point as the endpoint varies along a small curve segment through data recorded in the Jacobi field, a vector field along the geodesic. One and a quarter centuries after Gauss and Jacobi, Marston Morse gave a more conceptual interpretation of the Jacobi field in terms of second derivatives of the energy function on the infinite-dimensional Hilbert manifold of paths.

Exponential map

The theory of ordinary differential equations shows that if is smooth then the differential equation with initial condition has a unique solution for sufficiently small and the solution depends smoothly on and . This implies that for sufficiently small tangent vectors at a given point , there is a geodesic defined on with and . Moreover, if , then . The '' exponential map'' is defined by
: (1)
and gives a diffeomorphism between a disc and a neighbourhood of ; more generally the map sending to gives a local diffeomorphism onto a neighbourhood of . The exponential map gives '' geodesic normal coordinates'' near .

Computation of normal coordinates

There is a standard technique (see for example ) for computing the change of variables to normal coordinates , at a point as a formal Taylor series expansion. If the coordinates , at (0,0) are locally orthogonal, write
:
:
where , are quadratic and , cubic homogeneous polynomials in and . If and are fixed, and can be considered as formal power series solutions of the Euler equations: this uniquely determines , , , , and .

Gauss's lemma

In these coordinates the matrix satisfies and the lines are geodesics through 0. Euler's equations imply the matrix equation
:,
a key result, usually called the Gauss lemma. Geometrically it states that
:

Taking polar coordinates , it follows that the metric has the form
:.
In geodesic coordinates, it is easy to check that the geodesics through zero minimize length. The topology on the Riemannian manifold is then given by a distance function , namely the infimum of the lengths of piecewise smooth paths between and . This distance is realised locally by geodesics, so that in normal coordinates . If the radius is taken small enough, a slight sharpening of the Gauss lemma shows that the image of the disc under the exponential map is geodesically convex, i.e. any two points in are joined by a unique geodesic lying entirely inside .

Theorema Egregium

Gauss's Theorema Egregium, the "Remarkable Theorem", shows that the Gaussian curvature of a surface can be computed solely in terms of the metric and is thus an intrinsic invariant of the surface, independent of any isometric embedding in and unchanged under coordinate transformations. In particular, isometries and local isometries of surfaces preserve Gaussian curvature.

This theorem can expressed in terms of the power series expansion of the metric, , is given in normal coordinates as
:.

Gauss–Jacobi equation

Taking a coordinate change from normal coordinates at to normal coordinates at a nearby point , yields the Sturm–Liouville equation satisfied by , discovered by Gauss and later generalised by Jacobi,
:.

The Jacobian of this coordinate change at is equal to . This gives another way of establishing the intrinsic nature of Gaussian curvature. Because can be interpreted as the length of the line element in the direction, the Gauss–Jacobi equation shows that the Gaussian curvature measures the spreading of geodesics on a geometric surface as they move away from a point.

Laplace–Beltrami operator

On a surface with local metric
:$ds^2 = E \, dx^2 + 2F \, dx \, dy + G \, dy^2$
and Laplace–Beltrami operator
:$\Delta f = \left(\partial_x \partial_x f - \partial_x \partial_y f -\partial_y \partial_x f + \partial_y \partial_yf\right),$
where , the Gaussian curvature at a point is given by the formula
:$K=- 3 \lim_ \Delta (\log r),$
where denotes the geodesic distance from the point.

In isothermal coordinates, first considered by Gauss, the metric is required to be of the special form
:$ds^2 = e^\varphi (dx^2+dy^2). \,$
In this case the Laplace–Beltrami operator is given by
:$\Delta = e^ \left(\frac + \frac\right)$
and satisfies Liouville's equation
:$\Delta \varphi=-2K. \,$

Isothermal coordinates are known to exist in a neighbourhood of any point on the surface, although all proofs to date rely on non-trivial results on partial differential equations. There is an elementary proof for minimal surfaces.

Gauss–Bonnet theorem

On a sphere or a hyperboloid, the area of a geodesic triangle, i.e. a triangle all the sides of which are geodesics, is proportional to the difference of the sum of the interior angles and . The constant of proportionality is just the Gaussian curvature, a constant for these surfaces. For the torus, the difference is zero, reflecting the fact that its Gaussian curvature is zero. These are standard results in spherical, hyperbolic and high school trigonometry (see below). Gauss generalised these results to an arbitrary surface by showing that the integral of the Gaussian curvature over the interior of a geodesic triangle is also equal to this angle difference or excess. His formula showed that the Gaussian curvature could be calculated near a point as the limit of area over angle excess for geodesic triangles shrinking to the point. Since any closed surface can be decomposed up into geodesic triangles, the formula could also be used to compute the integral of the curvature over the whole surface. As a special case of what is now called the Gauss–Bonnet theorem, Gauss proved that this integral was remarkably always 2π times an integer, a topological invariant of the surface called the Euler characteristic. This invariant is easy to compute combinatorially in terms of the number of vertices, edges, and faces of the triangles in the decomposition, also called a triangulation. This interaction between analysis and topology was the forerunner of many later results in geometry, culminating in the Atiyah-Singer index theorem. In particular properties of the curvature impose restrictions on the topology of the surface.

Geodesic triangles

Gauss proved that, if is a geodesic triangle on a surface with angles , and at vertices , and , then
:$\int_\Delta K\,dA = \alpha + \beta + \gamma - \pi.$

In fact taking geodesic polar coordinates with origin and , the radii at polar angles 0 and :
:$\begin \int_\Delta K\,dA &= \int_\Delta KH\,dr\,d\theta = - \int_0^\alpha \int_0^ \! H_\,dr\,d\theta \\ &= \int_0^\alpha 1 -H_r(r_\theta,\theta)\,d\theta = \int_0^\alpha d\theta + \int_^\gamma \!\! d\varphi \\ &= \alpha + \beta + \gamma - \pi, \end$
where the second equality follows from the Gauss–Jacobi equation and the fourth from Gauss's derivative formula in the orthogonal coordinates .

Gauss's formula shows that the curvature at a point can be calculated as the limit of ''angle excess'' over ''area'' for successively smaller geodesic triangles near the point. Qualitatively a surface is positively or negatively curved according to the sign of the angle excess for arbitrarily small geodesic triangles.

Gauss–Bonnet theorem

Since every compact oriented 2-manifold can be triangulated by small geodesic triangles, it follows that
:$\int_M K dA = 2\pi\,\chi(M)$
where denotes the Euler characteristic of the surface.

In fact if there are faces, edges and vertices, then and the left hand side equals .

This is the celebrated Gauss–Bonnet theorem: it shows that the integral of the Gaussian curvature is a topological invariant of the manifold, namely the Euler characteristic. This theorem can be interpreted in many ways; perhaps one of the most far-reaching has been as the index theorem for an elliptic differential operator on , one of the simplest cases of the Atiyah-Singer index theorem. Another related result, which can be proved using the Gauss–Bonnet theorem, is the Poincaré-Hopf index theorem for vector fields on which vanish at only a finite number of points: the sum of the indices at these points equals the Euler characteristic, where the ''index'' of a point is defined as follows: on a small circle round each isolated zero, the vector field defines a map into the unit circle; the index is just the winding number of this map.)

Curvature and embeddings

If the Gaussian curvature of a surface is everywhere positive, then the Euler characteristic is positive so is homeomorphic (and therefore diffeomorphic) to . If in addition the surface is isometrically embedded in , the Gauss map provides an explicit diffeomorphism. As Hadamard observed, in this case the surface is convex; this criterion for convexity can be viewed as a 2-dimensional generalisation of the well-known second derivative criterion for convexity of plane curves. Hilbert proved that every isometrically embedded closed surface must have a point of positive curvature. Thus a closed Riemannian 2-manifold of non-positive curvature can never be embedded isometrically in ; however, as Adriano Garsia showed using the Beltrami equation for quasiconformal mappings, this is always possible for some conformally equivalent metric.;

Surfaces of constant curvature

The simply connected surfaces of constant curvature 0, +1 and –1 are the Euclidean plane, the unit sphere in , and the hyperbolic plane. Each of these has a transitive three-dimensional Lie group of orientation preserving isometries , which can be used to study their geometry. Each of the two non-compact surfaces can be identified with the quotient where is a maximal compact subgroup of . Here is isomorphic to . Any other closed Riemannian 2-manifold of constant Gaussian curvature, after scaling the metric by a constant factor if necessary, will have one of these three surfaces as its universal covering space. In the orientable case, the fundamental group of can be identified with a torsion-free uniform subgroup of and can then be identified with the double coset space . In the case of the sphere and the Euclidean plane, the only possible examples are the sphere itself and tori obtained as quotients of by discrete rank 2 subgroups. For closed surfaces of genus , the moduli space of Riemann surfaces obtained as varies over all such subgroups, has real dimension . By Poincaré's uniformization theorem, any orientable closed 2-manifold is conformally equivalent to a surface of constant curvature 0, +1 or –1. In other words, by multiplying the metric by a positive scaling factor, the Gaussian curvature can be made to take exactly one of these values (the sign of the Euler characteristic of ).

Euclidean geometry

In the case of the Euclidean plane, the symmetry group is the Euclidean motion group, the semidirect product of
the two dimensional group of translations by the group of rotations. Geodesics are straight lines and the geometry is encoded in the elementary formulas of trigonometry, such as the cosine rule for a triangle with sides , , and angles , , :
:$c^2 = a^2 +b^2 -2ab \,\cos \gamma.$

Flat tori can be obtained by taking the quotient of by a lattice, i.e. a free Abelian subgroup of rank 2. These closed surfaces have no isometric embeddings in . They do nevertheless admit isometric embeddings in ; in the easiest case this follows from the fact that the torus is a product of two circles and each circle can be isometrically embedded in .

Spherical geometry

The isometry group of the unit sphere in is the orthogonal group , with the rotation group as the subgroup of isometries preserving orientation. It is the direct product of with the antipodal map, sending to . The group acts transitively on . The stabilizer subgroup of the unit vector (0,0,1) can be identified with , so that .

The geodesics between two points on the sphere are the great circle arcs with these given endpoints. If the points are not antipodal, there is a unique shortest geodesic between the points. The geodesics can also be described group theoretically: each geodesic through the North pole (0,0,1) is the orbit of the subgroup of rotations about an axis through antipodal points on the equator.

A spherical triangle is a geodesic triangle on the sphere. It is defined by points , , on the sphere with sides , , formed from great circle arcs of length less than . If the lengths of the sides are , , and the angles between the sides , , , then the spherical cosine law states that
:$\cos c = \cos a \, \cos b + \sin a\, \sin b \,\cos \gamma.$
The area of the triangle is given by
:.

Using stereographic projection from the North pole, the sphere can be identified with the extended complex plane . The explicit map is given by
:$\pi(x,y,z)=\equiv u + iv.$

Under this correspondence every rotation of corresponds to a Möbius transformation in , unique up to sign. With respect to the coordinates in the complex plane, the spherical metric becomes
:$ds^2 = .$

The unit sphere is the unique closed orientable surface with constant curvature +1. The quotient can be identified with the real projective plane. It is non-orientable and can be described as the quotient of by the antipodal map (multiplication by −1). The sphere is simply connected, while the real projective plane has fundamental group . The finite subgroups of , corresponding to the finite subgroups of and the symmetry groups of the platonic solids, do not act freely on , so the corresponding quotients are not 2-manifolds, just orbifolds.

Hyperbolic geometry

Non-Euclidean geometry was first discussed in letters of Gauss, who made extensive computations at the turn of the nineteenth century which, although privately circulated, he decided not to put into print. In 1830 Lobachevsky and independently in 1832 Bolyai, the son of one Gauss's correspondents, published synthetic versions of this new geometry, for which they were severely criticized. However it was not until 1868 that Beltrami, followed by Klein in 1871 and Poincaré in 1882, gave concrete analytic models for what Klein dubbed hyperbolic geometry. The four models of 2-dimensional hyperbolic geometry that emerged were:
*the Beltrami-Klein model;
*the Poincaré disk;
*the Poincaré upper half-plane;
*the hyperboloid model of Wilhelm Killing in 3-dimensional Minkowski space.

The first model, based on a disk, has the advantage that geodesics are actually line segments (that is, intersections of Euclidean lines with the open unit disk). The last model has the advantage that it gives a construction which is completely parallel to that of the unit sphere in 3-dimensional Euclidean space. Because of their application in complex analysis and geometry, however, the models of Poincaré are the most widely used: they are interchangeable thanks to the Möbius transformations between the disk and the upper half-plane.

Let
:$D=\$
be the Poincaré disk in the complex plane with Poincaré metric
:$ds^2= .$
In polar coordinates the metric is given by
:$ds^2= .$

The length of a curve is given by the formula
:$\ell(\gamma)=\int_a^b .$

The group given by
:$G=\left\$
acts transitively by Möbius transformations on and the stabilizer subgroup of 0 is the rotation group
:$K=\left\.$

The quotient group is the group of orientation-preserving isometries of . Any two points , in are joined by a unique geodesic, given by the portion of the circle or straight line passing through and and orthogonal to the boundary circle. The distance between and is given by
:$d(z,w)=2 \tanh^ \frac.$

In particular and is the geodesic through 0 along the real axis, parametrized by arclength.

The topology defined by this metric is equivalent to the usual Euclidean topology, although as a metric space is complete.

A hyperbolic triangle is a geodesic triangle for this metric: any three points in are vertices of a hyperbolic triangle. If the sides have length , , with corresponding angles , , , then the hyperbolic cosine rule states that
:$\cosh c = \cosh a\, \cosh b - \sinh a \,\sinh b \,\cos \gamma.$

The area of the hyperbolic triangle is given by
:.

The unit disk and the upper half-plane
:$H=\$
are conformally equivalent by the Möbius transformations
:$w=i ,\,\, z=.$

Under this correspondence the action of by Möbius transformations on corresponds to that of on . The metric on becomes
:$ds^2 = .$

Since lines or circles are preserved under Möbius transformations, geodesics are again described by lines or circles orthogonal to the real axis.

The unit disk with the Poincaré metric is the unique simply connected oriented 2-dimensional Riemannian manifold with constant curvature −1. Any oriented closed surface with this property has as its universal covering space. Its fundamental group can be identified with a torsion-free concompact subgroup of , in such a way that
:$M= \Gamma\backslash G /K.$
In this case is a finitely presented group. The generators and relations are encoded in a geodesically convex fundamental geodesic polygon in (or ) corresponding geometrically to closed geodesics on .

Examples.
* the Bolza surface of genus 2;
* the Klein quartic of genus 3;
* the Macbeath surface of genus 7;
* the First Hurwitz triplet of genus 14.

Uniformization

Given an oriented closed surface with Gaussian curvature , the metric on can be changed conformally by scaling it by a factor . The new Gaussian curvature is then given by
:$K^\prime(x)= e^ (K(x) - \Delta u),$
where is the Laplacian for the original metric. Thus to show that a given surface is conformally equivalent to a metric with constant curvature it suffices to solve the following variant of Liouville's equation:
:$\Delta u = K^\prime e^ + K(x).$

When has Euler characteristic 0, so is diffeomorphic to a torus, , so this amounts to solving
:$\Delta u = K(x).$

By standard elliptic theory, this is possible because the integral of over is zero, by the Gauss–Bonnet theorem.

When has negative Euler characteristic, , so the equation to be solved is:
:$\Delta u = -e^ + K(x).$
Using the continuity of the exponential map on Sobolev space due to Neil Trudinger, this non-linear equation can always be solved.

Finally in the case of the 2-sphere, and the equation becomes:
:$\Delta u = e^ + K(x).$
So far this non-linear equation has not been analysed directly, although classical results such as the Riemann–Roch theorem imply that it always has a solution. The method of Ricci flow, developed by Richard S. Hamilton, gives another proof of existence based on non-linear partial differential equations to prove existence. In fact the Ricci flow on conformal metrics on is defined on functions by
:$u_t = 4\pi - K'(x,t) = 4\pi -e^ (K(x) - \Delta u).$
After finite time, Chow showed that becomes positive; previous results of Hamilton could then be used to show that converges to +1. Prior to these results on Ricci flow, had given an alternative and technically simpler approach to uniformization based on the flow on Riemannian metrics defined by .

A proof using elliptic operators, discovered in 1988, can be found in . Let be the Green's function on satisfying , where is the point measure at a fixed point of . The equation , has a smooth solution , because the right hand side has integral 0 by the Gauss–Bonnet theorem. Thus satisfies away from . It follows that is a complete metric of constant curvature 0 on the complement of , which is therefore isometric to the plane. Composing with stereographic projection, it follows that there is a smooth function such that has Gaussian curvature +1 on the complement of . The function automatically extends to a smooth function on the whole of .

Riemannian connection and parallel transport

The classical approach of Gauss to the differential geometry of surfaces was the standard elementary approach which predated the emergence of the concepts of Riemannian manifold initiated by Bernhard Riemann in the mid-nineteenth century and of connection developed by Tullio Levi-Civita, Élie Cartan and Hermann Weyl in the early twentieth century. The notion of connection, covariant derivative and parallel transport gave a more conceptual and uniform way of understanding curvature, which not only allowed generalisations to higher dimensional manifolds but also provided an important tool for defining new geometric invariants, called characteristic classes. The approach using covariant derivatives and connections is nowadays the one adopted in more advanced textbooks.

Covariant derivative

Connections on a surface can be defined from various equivalent but equally important points of view. The Riemannian connection or Levi-Civita connection. is perhaps most easily understood in terms of lifting vector fields, considered as first order differential operators acting on functions on the manifold, to differential operators on the tangent bundle or frame bundle. In the case of an embedded surface, the lift to an operator on vector fields, called the covariant derivative, is very simply described in terms of orthogonal projection. Indeed, a vector field on a surface embedded in can be regarded as a function from the surface into . Another vector field acts as a differential operator component-wise. The resulting vector field will not be tangent to the surface, but this can be corrected taking its orthogonal projection onto the tangent space at each point of the surface. As Ricci and Levi-Civita realised at the turn of the twentieth century, this process depends only on the metric and can be locally expressed in terms of the Christoffel symbols.

Parallel transport

Parallel transport of tangent vectors along a curve in the surface was the next major advance in the subject, due to Levi-Civita. It is related to the earlier notion of covariant derivative, because it is the monodromy of the ordinary differential equation on the curve defined by the covariant derivative with respect to the velocity vector of the curve. Parallel transport along geodesics, the "straight lines" of the surface, can also easily be described directly. A vector in the tangent plane is transported along a geodesic as the unique vector field with constant length and making a constant angle with the velocity vector of the geodesic. For a general curve, this process has to be modified using the geodesic curvature, which measures how far the curve departs from being a geodesic.

A vector field along a unit speed curve , with geodesic curvature , is said to be parallel along the curve if
* it has constant length
* the angle that it makes with the velocity vector satisfies
:$\dot(t) = - k_g(t)$

This recaptures the rule for parallel transport along a geodesic or piecewise geodesic curve, because in that case , so that the angle should remain constant on any geodesic segment. The existence of parallel transport follows because can be computed as the integral of the geodesic curvature. Since it therefore depends continuously on the norm of , it follows that parallel transport for an arbitrary curve can be obtained as the limit of the parallel transport on approximating piecewise geodesic curves.

The connection can thus be described in terms of lifting paths in the manifold to paths in the tangent or orthonormal frame bundle, thus formalising the classical theory of the "moving frame", favoured by French authors. Lifts of loops about a point give rise to the holonomy group at that point. The Gaussian curvature at a point can be recovered from parallel transport around increasingly small loops at the point. Equivalently curvature can be calculated directly at an infinitesimal level in terms of Lie brackets of lifted vector fields.

Connection 1-form

The approach of Cartan and Weyl, using connection 1-forms on the frame bundle of , gives a third way to understand the Riemannian connection. They noticed that parallel transport dictates that a path in the surface be lifted to a path in the frame bundle so that its tangent vectors lie in a special subspace of codimension one in the three-dimensional tangent space of the frame bundle. The projection onto this subspace is defined by a differential 1-form on the orthonormal frame bundle, the connection form. This enabled the curvature properties of the surface to be encoded in differential forms on the frame bundle and formulas involving their exterior derivatives.

This approach is particularly simple for an embedded surface. Thanks to a result of , the connection 1-form on a surface embedded in Euclidean space is just the pullback under the Gauss map of the connection 1-form on . Using the identification of with the homogeneous space , the connection 1-form is just a component of the Maurer–Cartan 1-form on .

Global differential geometry of surfaces

Although the characterisation of curvature involves only the local geometry of a surface, there are important global aspects such as the Gauss–Bonnet theorem, the uniformization theorem, the von Mangoldt-Hadamard theorem, and the embeddability theorem. There are other important aspects of the global geometry of surfaces. These include:

* Injectivity radius, defined as the largest such that two points at a distance less than are joined by a unique geodesic. Wilhelm Klingenberg proved in 1959 that the injectivity radius of a closed surface is bounded below by the minimum of and the length of its smallest closed geodesic. This improved a theorem of Bonnet who showed in 1855 that the diameter of a closed surface of positive Gaussian curvature is always bounded above by ; in other words a geodesic realising the metric distance between two points cannot have length greater than .
*Rigidity. In 1927 Cohn-Vossen proved that two ovaloids – closed surfaces with positive Gaussian curvature – that are isometric are necessarily congruent by an isometry of . Moreover, a closed embedded surface with positive Gaussian curvature and constant mean curvature is necessarily a sphere; likewise a closed embedded surface of constant Gaussian curvature must be a sphere (Liebmann 1899). Heinz Hopf showed in 1950 that a closed embedded surface with constant mean curvature and genus 0, i.e. homeomorphic to a sphere, is necessarily a sphere; five years later Alexandrov removed the topological assumption. In the 1980s, Wente constructed immersed tori of constant mean curvature in Euclidean 3-space.
* Carathéodory conjecture: This conjecture states that a closed convex three times differentiable surface admits at least two umbilic points. The first work on this conjecture was in 1924 by Hans Hamburger, who noted that it follows from the following stronger claim: the half-integer valued index of the principal curvature foliation of an isolated umbilic is at most one. It was proven for smooth surfaces by Brendan Guilfoyle and Wilhelm Klingenberg in three parts concluding in 2024, the centenary of the conjecture.
*Zero Gaussian curvature: a complete surface in with zero Gaussian curvature must be a cylinder or a plane.
*Hilbert's theorem (1901): no complete surface with constant negative curvature can be immersed isometrically in .

*The Willmore conjecture. This conjecture states that the integral of the square of the mean curvature of a torus immersed in should be bounded below by . It is known that the integral is Moebius invariant. It was solved in 2012 by Fernando Codá Marques and André Neves.
* Isoperimetric inequalities. In 1939 Schmidt proved that the classical isoperimetric inequality for curves in the Euclidean plane is also valid on the sphere or in the hyperbolic plane: namely he showed that among all closed curves bounding a domain of fixed area, the perimeter is minimized by when the curve is a circle for the metric. In one dimension higher, it is known that among all closed surfaces in arising as the boundary of a bounded domain of unit volume, the surface area is minimized for a Euclidean ball.
* Systolic inequalities for curves on surfaces. Given a closed surface, its systole is defined to be the smallest length of any non-contractible closed curve on the surface. In 1949 Loewner proved a torus inequality for metrics on the torus, namely that the area of the torus over the square of its systole is bounded below by , with equality in the flat (constant curvature) case. A similar result is given by Pu's inequality for the real projective plane from 1952, with a lower bound of also attained in the constant curvature case. For the Klein bottle, Blatter and Bavard later obtained a lower bound of . For a closed surface of genus , Hebda and Burago showed that the ratio is bounded below by . Three years later Mikhail Gromov found a lower bound given by a constant times , although this is not optimal. Asymptotically sharp upper and lower bounds given by constant times are due to Gromov and Buser-Sarnak, and can be found in . There is also a version for metrics on the sphere, taking for the systole the length of the smallest closed geodesic. Gromov conjectured a lower bound of in 1980: the best result so far is the lower bound of obtained by Regina Rotman in 2006.Rotman, R. (2006) "The length of a shortest closed geodesic and the area of a 2-dimensional sphere", Proc. Amer. Math. Soc. 134: 3041-3047. Previous lower bounds had been obtained by Croke, Rotman-Nabutovsky and Sabourau.

Reading guide

One of the most comprehensive introductory surveys of the subject, charting the historical development from before Gauss to modern times, is by . Accounts of the classical theory are given in , and ; the more modern copiously illustrated undergraduate textbooks by , and might be found more accessible. An accessible account of the classical theory can be found in . More sophisticated graduate-level treatments using the Riemannian connection on a surface can be found in , and .

See also

*Tangent vector
*Zoll surface

Notes

References

*
*; translated from the Russian by K. Vogtmann and A. Weinstein.
*
*
*
*
*; translated from 2nd edition of '' Leçons sur la géométrie des espaces de Riemann'' (1951) by James Glazebrook.
*; translated from Russian by V. V. Goldberg with a foreword by S. S. Chern.
*
*
*
*
*

Volume I (1887)Volume II (1915) [1889
/nowiki>">889">Volume II (1915) [1889
/nowiki>br>Volume III (1894)Volume IV (1896)

*
*
*
*
*.
*.
* translated by A.M. Hiltebeitel and J.C. Morehead
"Disquisitiones generales circa superficies curvas"
''Commentationes Societatis Regiae Scientiarum Gottingesis Recentiores'' Vol. VI (1827), pp. 99–146.
**.
**.
*
*
*
*
*
*
*
*
*
*
*
*,
*
*
*
*
*
*
*
*
* Ian R. Porteous (2001) ''Geometric Differentiation: for the intelligence of curves and surfaces'', Cambridge University Press .
*
*
*
*
*
*
*
*
*
*
*

Full text of book
*
*
*

External links

*

{{DEFAULTSORT:Differential Geometry Of Surfaces