Second-order cone programming on:
[Wikipedia]
[Google]
[Amazon]
A second-order cone program (SOCP) is a
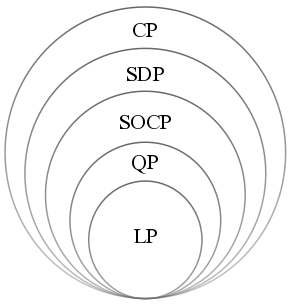 When for , the SOCP reduces to a linear program. When for , the SOCP is equivalent to a convex quadratically constrained linear program.
Convex quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint. Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semidefinite program. The converse, however, is not valid: there are positive semidefinite cones that do not admit any second-order cone representation.
Any closed convex semialgebraic set in the plane can be written as a feasible region of a SOCP,. However, it is known that there exist convex semialgebraic sets of higher dimension that are not representable by SDPs; that is, there exist convex semialgebraic sets that can not be written as the feasible region of a SDP (nor, a fortiori, as the feasible region of a SOCP).
When for , the SOCP reduces to a linear program. When for , the SOCP is equivalent to a convex quadratically constrained linear program.
Convex quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint. Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semidefinite program. The converse, however, is not valid: there are positive semidefinite cones that do not admit any second-order cone representation.
Any closed convex semialgebraic set in the plane can be written as a feasible region of a SOCP,. However, it is known that there exist convex semialgebraic sets of higher dimension that are not representable by SDPs; that is, there exist convex semialgebraic sets that can not be written as the feasible region of a SDP (nor, a fortiori, as the feasible region of a SOCP).
convex optimization
Convex optimization is a subfield of mathematical optimization that studies the problem of minimizing convex functions over convex sets (or, equivalently, maximizing concave functions over convex sets). Many classes of convex optimization problems ...
problem of the form
:minimize
:subject to
::
::
where the problem parameters are , and . is the optimization variable.
is the Euclidean norm and indicates transpose
In linear algebra, the transpose of a Matrix (mathematics), matrix is an operator which flips a matrix over its diagonal;
that is, it switches the row and column indices of the matrix by producing another matrix, often denoted by (among other ...
. The "second-order cone" in SOCP arises from the constraints, which are equivalent to requiring the affine function to lie in the second-order cone in .
SOCPs can be solved by interior point methods and in general, can be solved more efficiently than semidefinite programming (SDP) problems. Some engineering applications of SOCP include filter design, antenna array weight design, truss design, and grasping force optimization in robotics. Applications in quantitative finance include portfolio optimization; some market impact constraints, because they are not linear, cannot be solved by quadratic programming but can be formulated as SOCP problems.
Second-order cone
The standard or unit second-order cone of dimension is defined as . The second-order cone is also known by quadratic cone or ice-cream cone or Lorentz cone. The standard second-order cone in is . The set of points satisfying a second-order cone constraint is the inverse image of the unit second-order cone under an affine mapping: and hence is convex. The second-order cone can be embedded in the cone of the positive semidefinite matrices since i.e., a second-order cone constraint is equivalent to a linear matrix inequality (Here means is semidefinite matrix). Similarly, we also have, .Relation with other optimization problems
 When for , the SOCP reduces to a linear program. When for , the SOCP is equivalent to a convex quadratically constrained linear program.
Convex quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint. Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semidefinite program. The converse, however, is not valid: there are positive semidefinite cones that do not admit any second-order cone representation.
Any closed convex semialgebraic set in the plane can be written as a feasible region of a SOCP,. However, it is known that there exist convex semialgebraic sets of higher dimension that are not representable by SDPs; that is, there exist convex semialgebraic sets that can not be written as the feasible region of a SDP (nor, a fortiori, as the feasible region of a SOCP).
When for , the SOCP reduces to a linear program. When for , the SOCP is equivalent to a convex quadratically constrained linear program.
Convex quadratically constrained quadratic programs can also be formulated as SOCPs by reformulating the objective function as a constraint. Semidefinite programming subsumes SOCPs as the SOCP constraints can be written as linear matrix inequalities (LMI) and can be reformulated as an instance of semidefinite program. The converse, however, is not valid: there are positive semidefinite cones that do not admit any second-order cone representation.
Any closed convex semialgebraic set in the plane can be written as a feasible region of a SOCP,. However, it is known that there exist convex semialgebraic sets of higher dimension that are not representable by SDPs; that is, there exist convex semialgebraic sets that can not be written as the feasible region of a SDP (nor, a fortiori, as the feasible region of a SOCP).
Examples
Quadratic constraint
Consider a convex quadratic constraint of the form : This is equivalent to the SOCP constraint :Stochastic linear programming
Consider a stochastic linear program in inequality form :minimize :subject to :: where the parameters are independent Gaussian random vectors with mean and covariance and . This problem can be expressed as the SOCP :minimize :subject to :: where is the inverse normal cumulative distribution function.Stochastic second-order cone programming
We refer to second-order cone programs as deterministic second-order cone programs since data defining them are deterministic. Stochastic second-order cone programs are a class of optimization problems that are defined to handle uncertainty in data defining deterministic second-order cone programs.Other examples
Other modeling examples are available at the MOSEK modeling cookbook.Solvers and scripting (programming) languages
See also
* Power cones are generalizations of quadratic cones to powers other than 2.References
{{reflist Optimization algorithms and methods Convex optimization