Regular Heptagon on:
[Wikipedia]
[Google]
[Amazon]
In
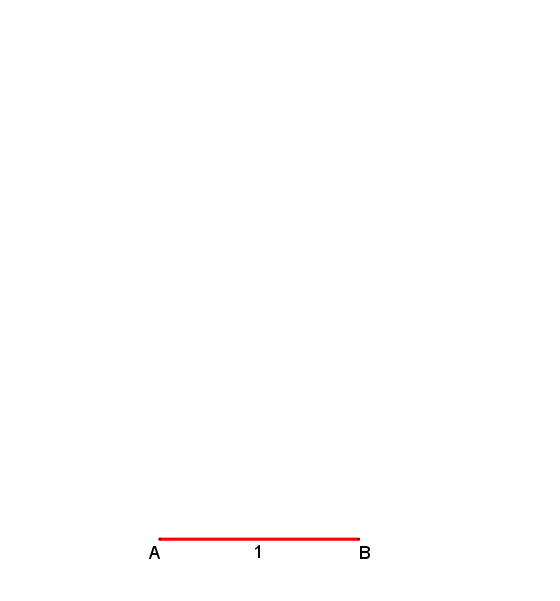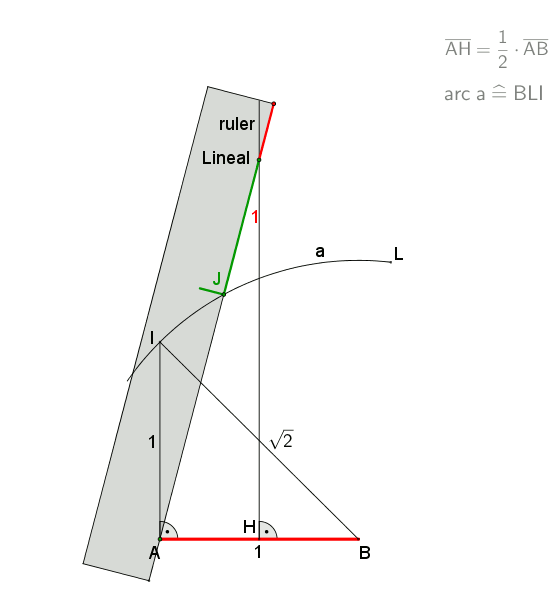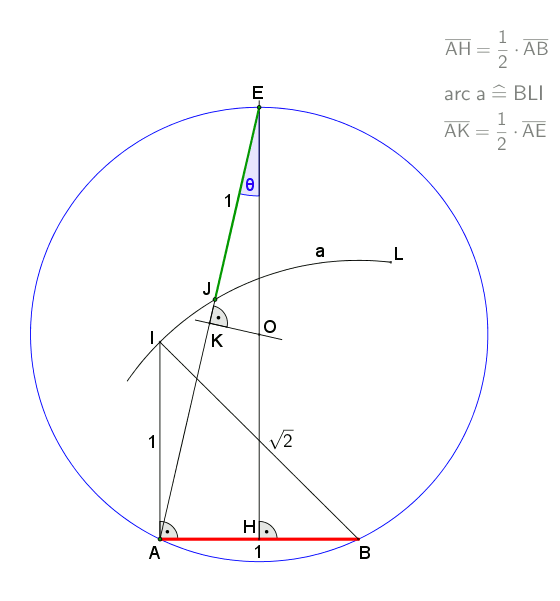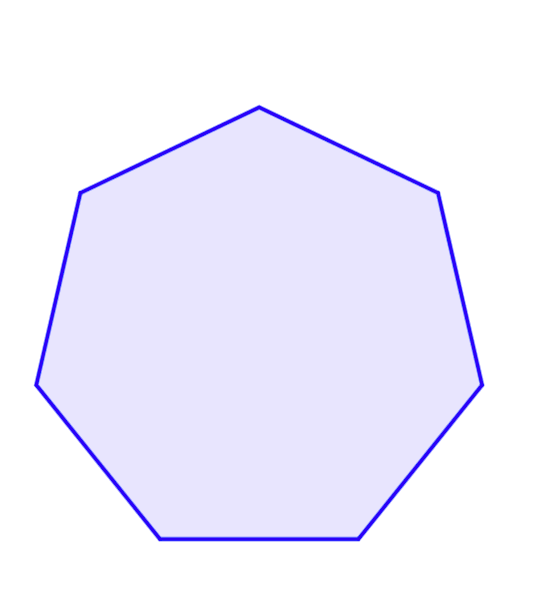
At a circumscribed circle radius ''r = 1 m'', the absolute error of the 1st side would be ''approximately -1.7 mm''
 The ''regular heptagon'' belongs to the D7h
The ''regular heptagon'' belongs to the D7h
 The regular heptagon's side ''a'', shorter
The regular heptagon's side ''a'', shorter

Blue, and green star heptagons inside a red heptagon.
 The United Kingdom, , has two heptagonal
The United Kingdom, , has two heptagonal
Definition and properties of a heptagon
With interactive animation
Heptagon according Johnson
Another approximate construction method
Recently discovered and highly accurate approximation for the construction of a regular heptagon.
* Heptagon, an approximating construction as an animation * A heptagon with a given side, an approximating construction as an animation {{Polygons Polygons by the number of sides 7 (number) Elementary shapes
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a heptagon or septagon is a seven-sided polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...
or 7-gon.
The heptagon is sometimes referred to as the septagon, using "sept-" (an elision
In linguistics, an elision or deletion is the omission of one or more sounds (such as a vowel, a consonant, or a whole syllable) in a word or phrase. However, these terms are also used to refer more narrowly to cases where two words are run toget ...
of '' septua-'', a Latin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power ...
-derived numerical prefix
Numeral or number prefixes are prefixes derived from numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example:
* unicycle, bicycle, tricycle (1-cycle, 2-cycle, 3-cyc ...
, rather than '' hepta-'', a Greek
Greek may refer to:
Greece
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group.
*Greek language, a branch of the Indo-European language family.
**Proto-Greek language, the assumed last common ancestor ...
-derived numerical prefix; both are cognate) together with the Greek suffix "-agon" meaning angle.
Regular heptagon
Aregular
The term regular can mean normal or in accordance with rules. It may refer to:
People
* Moses Regular (born 1971), America football player
Arts, entertainment, and media Music
* "Regular" (Badfinger song)
* Regular tunings of stringed instrum ...
heptagon, in which all sides and all angles are equal, has internal angle
In geometry, an angle of a polygon is formed by two sides of the polygon that share an endpoint. For a simple (non-self-intersecting) polygon, regardless of whether it is convex or non-convex, this angle is called an interior angle (or ) if ...
s of 5π/7 radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s (128 degree
Degree may refer to:
As a unit of measurement
* Degree (angle), a unit of angle measurement
** Degree of geographical latitude
** Degree of geographical longitude
* Degree symbol (°), a notation used in science, engineering, and mathemati ...
s). Its Schläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to mor ...
is .
Area
The area (''A'') of a regular heptagon of side length ''a'' is given by: : This can be seen by subdividing the unit-sided heptagon into seven triangular "pie slices" with vertices at the center and at the heptagon's vertices, and then halving each triangle using the apothem as the common side. The apothem is half thecotangent
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in ...
of and the area of each of the 14 small triangles is one-fourth of the apothem.
The area of a regular heptagon inscribed in a circle of radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the ...
''R'' is while the area of the circle itself is thus the regular heptagon fills approximately 0.8710 of its circumscribed circle.
Construction
As 7 is a Pierpont prime but not a Fermat prime, the regular heptagon is not constructible withcompass and straightedge
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
but is constructible with a marked ruler
A ruler, sometimes called a rule, line gauge, or scale, is a device used in geometry and technical drawing, as well as the engineering and construction industries, to measure distances or draw straight lines.
Variants
Rulers have long ...
and compass. It is the smallest regular polygon with this property. This type of construction is called a neusis construction. It is also constructible with compass, straightedge and angle trisector. The impossibility of straightedge and compass construction follows from the observation that is a zero of the irreducible cubic
Cubic may refer to:
Science and mathematics
* Cube (algebra), "cubic" measurement
* Cube, a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex
** Cubic crystal system, a crystal system w ...
. Consequently, this polynomial is the minimal polynomial of whereas the degree of the minimal polynomial for a constructible number
In geometry and algebra, a real number r is constructible if and only if, given a line segment of unit length, a line segment of length , r, can be constructed with compass and straightedge in a finite number of steps. Equivalently, r is cons ...
must be a power of 2.

Approximation
An approximation for practical use with an error of about 0.2% is shown in the drawing. It is attributed to Albrecht Dürer. Let ''A'' lie on the circumference of the circumcircle. Draw arc ''BOC''. Then gives an approximation for the edge of the heptagon. This approximation uses for the side of the heptagon inscribed in the unit circle while the exact value is . ''Example to illustrate the error:At a circumscribed circle radius ''r = 1 m'', the absolute error of the 1st side would be ''approximately -1.7 mm''

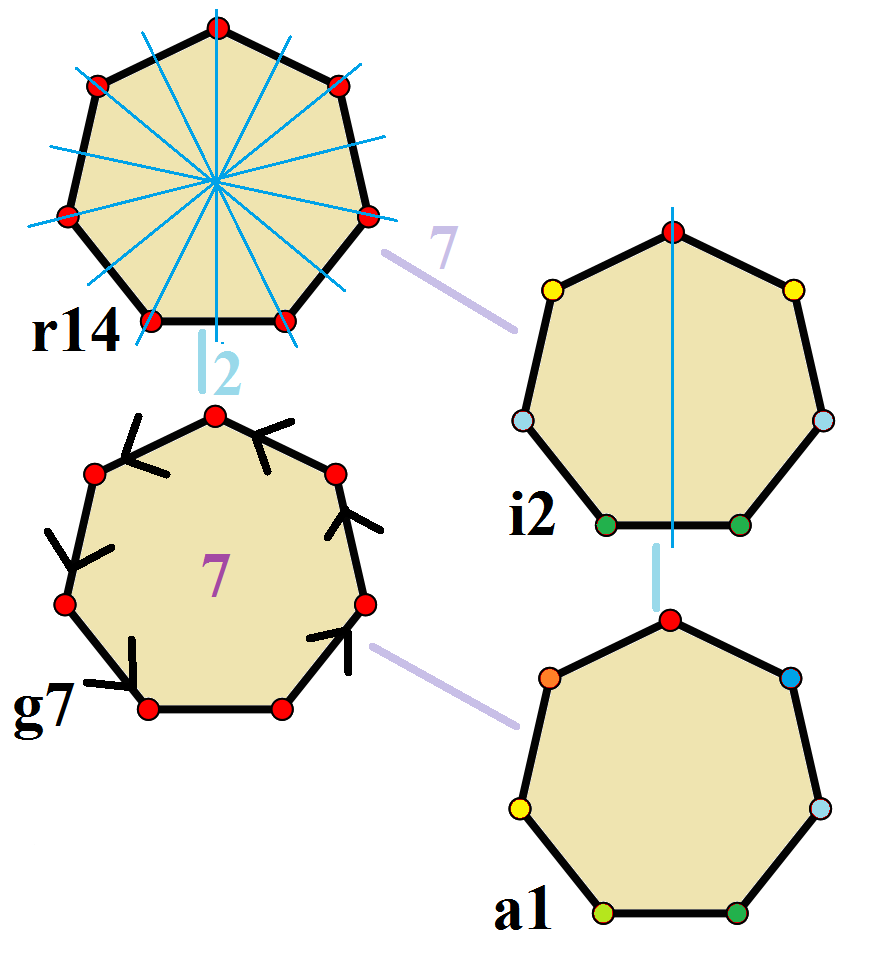
Symmetry
 The ''regular heptagon'' belongs to the D7h
The ''regular heptagon'' belongs to the D7h point group
In geometry, a point group is a mathematical group of symmetry operations ( isometries in a Euclidean space) that have a fixed point in common. The coordinate origin of the Euclidean space is conventionally taken to be a fixed point, and every ...
(Schoenflies notation The Schoenflies (or Schönflies) notation, named after the German mathematician Arthur Moritz Schoenflies, is a notation primarily used to specify point groups in three dimensions. Because a point group alone is completely adequate to describe the ...
), order 28. The symmetry elements are: a 7-fold proper rotation axis C7, a 7-fold improper rotation axis, S7, 7 vertical mirror planes, σv, 7 2-fold rotation axes, C2, in the plane of the heptagon and a horizontal mirror plane, σh, also in the heptagon's plane.
Diagonals and heptagonal triangle
diagonal
In geometry, a diagonal is a line segment joining two vertices of a polygon or polyhedron, when those vertices are not on the same edge. Informally, any sloping line is called diagonal. The word ''diagonal'' derives from the ancient Gree ...
''b'', and longer diagonal ''c'', with ''a''<''b''<''c'', satisfyAbdilkadir Altintas, "Some Collinearities in the Heptagonal Triangle", '' Forum Geometricorum'' 16, 2016, 249–256.http://forumgeom.fau.edu/FG2016volume16/FG201630.pdf
:
:
:
: (the optic equation
In number theory, the optic equation is an equation that requires the sum of the reciprocals of two positive integers ''a'' and ''b'' to equal the reciprocal of a third positive integer ''c'':Dickson, L. E., ''History of the Theory of Numbers, V ...
)
and hence
:
and
:
:
:
Thus –''b''/''c'', ''c''/''a'', and ''a''/''b'' all satisfy the cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of t ...
However, no algebraic expression In mathematics, an algebraic expression is an expression built up from integer constants, variables, and the algebraic operations ( addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number). ...
s with purely real terms exist for the solutions of this equation, because it is an example of casus irreducibilis.
The approximate lengths of the diagonals in terms of the side of the regular heptagon are given by
:
We also have
:
:
:
and
:
A heptagonal triangle has vertices coinciding with the first, second, and fourth vertices of a regular heptagon (from an arbitrary starting vertex) and angles and Thus its sides coincide with one side and two particular diagonals of the regular heptagon.
In polyhedra
Apart from the heptagonal prism and heptagonal antiprism, no convex polyhedron made entirely out of regular polygons contains a heptagon as a face.Star heptagons
Two kinds of star heptagons ( heptagrams) can be constructed from regular heptagons, labeled bySchläfli symbol
In geometry, the Schläfli symbol is a notation of the form \ that defines regular polytopes and tessellations.
The Schläfli symbol is named after the 19th-century Swiss mathematician Ludwig Schläfli, who generalized Euclidean geometry to mor ...
s , and , with the divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
being the interval of connection.
Blue, and green star heptagons inside a red heptagon.
Tiling and packing
A regular triangle, heptagon, and 42-gon can completely fill a plane vertex. However, there is no tiling of the plane with only these polygons, because there is no way to fit one of them onto the third side of the triangle without leaving a gap or creating an overlap. In the hyperbolic plane, tilings by regular heptagons are possible. The regular heptagon has a double lattice packing of the Euclidean plane of packing density approximately 0.89269. This has been conjectured to be the lowest density possible for the optimal double lattice packing density of any convex set, and more generally for the optimal packing density of any convex set.Empirical examples
 The United Kingdom, , has two heptagonal
The United Kingdom, , has two heptagonal coin
A coin is a small, flat (usually depending on the country or value), round piece of metal or plastic used primarily as a medium of exchange or legal tender. They are standardized in weight, and produced in large quantities at a mint in orde ...
s, the 50p and 20p pieces, and the Barbados Dollar are also heptagonal. The 20- eurocent coin has cavities placed similarly. Strictly, the shape of the coins is a Reuleaux heptagon, a curvilinear heptagon which has curves of constant width; the sides are curved outwards to allow the coins to roll smoothly when they are inserted into a vending machine
A vending machine is an automated machine that provides items such as snacks, beverages, cigarettes, and lottery tickets to consumers after cash, a credit card, or other forms of payment are inserted into the machine or otherwise made. The fir ...
. Botswana pula coins in the denominations of 2 Pula, 1 Pula, 50 Thebe and 5 Thebe are also shaped as equilateral-curve heptagons. Coins in the shape of Reuleaux heptagons are also in circulation in Mauritius, U.A.E., Tanzania, Samoa, Papua New Guinea, São Tomé and Príncipe, Haiti, Jamaica, Liberia, Ghana, the Gambia, Jordan, Jersey, Guernsey, Isle of Man, Gibraltar, Guyana, Solomon Islands, Falkland Islands and Saint Helena. The 1000 Kwacha coin of Zambia is a true heptagon.
The Brazil
Brazil ( pt, Brasil; ), officially the Federative Republic of Brazil (Portuguese: ), is the largest country in both South America and Latin America. At and with over 217 million people, Brazil is the world's fifth-largest country by area ...
ian 25-cent coin has a heptagon inscribed in the coin's disk. Some old versions of the coat of arms of Georgia
The coat of arms of Georgia is one of the national symbols of the republic. It is partially based on the medieval arms of the Georgian royal house and features Saint George, the traditional patron saint of Georgia. In addition to St. George, ...
, including in Soviet days, used a heptagram as an element.
In architecture, heptagonal floor plans are very rare. A remarkable example is the Mausoleum of Prince Ernst in Stadthagen, Germany
Germany, officially the Federal Republic of Germany (FRG),, is a country in Central Europe. It is the most populous member state of the European Union. Germany lies between the Baltic and North Sea to the north and the Alps to the sou ...
.
Many police badges in the US have a heptagram outline.
See also
* Heptagram *Polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...
References
External links
Definition and properties of a heptagon
With interactive animation
Heptagon according Johnson
Another approximate construction method
Recently discovered and highly accurate approximation for the construction of a regular heptagon.
* Heptagon, an approximating construction as an animation * A heptagon with a given side, an approximating construction as an animation {{Polygons Polygons by the number of sides 7 (number) Elementary shapes