rank (set theory)

In set theory and related branches of mathematics, the von Neumann universe, or von Neumann hierarchy of sets, denoted by ''V'', is the class of hereditary well-founded sets. This collection, which is formalized by Zermelo–Fraenkel set theory (ZFC), is often used to provide an interpretation or motivation of the axioms of ZFC. The concept is named after John von Neumann, although it was first published by Ernst Zermelo in 1930.

The rank of a well-founded set is defined inductively as the smallest ordinal number greater than the ranks of all members of the set. In particular, the rank of the empty set is zero, and every ordinal has a rank equal to itself. The sets in ''V'' are divided into the transfinite hierarchy ''V_α'', called the cumulative hierarchy, based on their rank.

Definition

The cumulative hierarchy is a collection of sets ''V''_α
indexed by the class of ordinal numbers; in particular, ''V''_α is the set of all sets having ranks less than α. Thus there is one set ''V''_α for each ordinal number α. ''V''_α may be defined by transfinite recursion as follows:

* Let ''V''₀ be the empty set:$V_0 := \varnothing .$
* For any ordinal number β, let ''V''_β+1 be the power set of ''V''_β:$V_ := \mathcal (V_\beta) .$
* For any limit ordinal λ, let ''V''_λ be the union of all the ''V''-stages so far:$V_\lambda := \bigcup_ V_\beta .$
A crucial fact about this definition is that there is a single formula φ(α,''x'') in the language of ZFC that states "the set ''x'' is in ''V''_α".

The sets ''V''_α are called stages or ranks.

The class ''V'' is defined to be the union of all the ''V''-stages:

$V := \bigcup_ V_\alpha.$

Rank of a set

The rank of a set ''S'' is the smallest α such that $S \subseteq V_\alpha \,.$ In other words, $\mathcal (V_\alpha)$ is the set of sets with rank ≤α. The stage ''V''_α can also be characterized as the set of sets with rank strictly less than α, regardless of whether α is 0, a successor ordinal, or a limit ordinal:

$V_\alpha := \bigcup_ \mathcal (V_\beta).$

This gives an equivalent definition of ''V''_α by transfinite recursion.

Substituting the above definition of ''V''_α back into the definition of the rank of a set gives a self-contained recursive definition:

In other words,

$\operatorname (S) = \bigcup \.$

Finite and low cardinality stages of the hierarchy

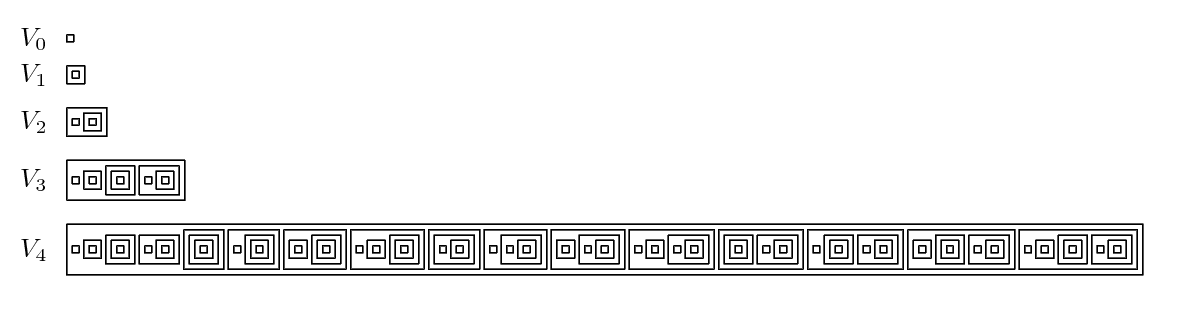
The first five von Neumann stages ''V''₀ to ''V''₄ may be visualized as follows. (An empty box represents the empty set. A box containing only an empty box represents the set containing only the empty set, and so forth.)

This sequence exhibits tetrational growth. The set ''V''₅ contains 2¹⁶ = 65536 elements; the set ''V''₆ contains 2⁶⁵⁵³⁶ elements, which very substantially exceeds the number of atoms in the known universe; and for any natural ''n'', the set ''V''_''n''+1 contains 2 ⇈ ''n'' elements using Knuth's up-arrow notation. So the finite stages of the cumulative hierarchy cannot be written down explicitly after stage 5. The set ''V''_ω has the same cardinality as ω. The set ''V''_ω+1 has the same cardinality as the set of real numbers.

Applications and interpretations

Applications of ''V'' as models for set theories

If ω is the set of natural numbers, then ''V''_ω is the set of hereditarily finite sets, which is a model of set theory without the axiom of infinity.

''V''_ω+ω is the universe of "ordinary mathematics", and is a model of Zermelo set theory (but not a model of ZF). A simple argument in favour of the adequacy of ''V''_ω+ω is the observation that ''V''_ω+1 is adequate for the integers, while ''V''_ω+2 is adequate for the real numbers, and most other normal mathematics can be built as relations of various kinds from these sets without needing the axiom of replacement to go outside ''V''_ω+ω.

If κ is an inaccessible cardinal, then ''V''_κ is a model of Zermelo–Fraenkel set theory (ZFC) itself, and ''V''_κ+1 is a model of Morse–Kelley set theory. (Note that every ZFC model is also a ZF model, and every ZF model is also a Z model.)

Interpretation of ''V'' as the "set of all sets"

V is not "the set of all (naive) sets" for two reasons. First, it is not a set; although each individual stage ''V''_α is a set, their union ''V'' is a proper class. Second, the sets in ''V'' are only the well-founded sets. The axiom of foundation (or regularity) demands that every set be well founded and hence in ''V'', and thus in ZFC every set is in ''V''. But other axiom systems may omit the axiom of foundation or replace it by a strong negation (an example is Aczel's anti-foundation axiom). These non-well-founded set theories are not commonly employed, but are still possible to study.

A third objection to the "set of all sets" interpretation is that not all sets are necessarily "pure sets", which are constructed from the empty set using power sets and unions. Zermelo proposed in 1908 the inclusion of urelements, from which he constructed a transfinite recursive hierarchy in 1930. Such urelements are used extensively in model theory, particularly in Fraenkel-Mostowski models..

Hilbert's paradox

The von Neumann universe satisfies the following two properties:

* $\mathcal(x) \in V$ for every ''set'' $x \in V$.
* $\bigcup x \in V$ for every ''subset'' $x \subseteq V$.

Indeed, if $x \in V$, then $x \in V_\alpha$ for some ordinal $\alpha$. Any stage is a transitive set, hence every $y \in x$ is already $y \in V_\alpha$, and so every subset of $x$ is a subset of $V_\alpha$. Therefore, $\mathcal(x) \subseteq V_$ and $\mathcal(x) \in V_ \subseteq V$. For unions of subsets, if $x \subseteq V$, then for every $y \in x$, let $\beta_y$ be the smallest ordinal for which $y \in V_$. Because by assumption $x$ is a set, we can form the limit $\alpha = \sup \$. The stages are cumulative, and therefore again every $y \in x$ is $y \in V_\alpha$. Then every $z \in y$ is also $z \in V_\alpha$, and so $\cup x \subseteq V_\alpha$ and $\cup x \in V_$.

Hilbert's paradox implies that no set with the above properties exists . For suppose $V$ was a set. Then $V$ would be a subset of itself, and $U = \cup V$ would belong to $V$, and so would $\mathcal(U)$. But more generally, if $A \in B$, then $A \subseteq \cup B$. Hence, $\mathcal(U) \subseteq \cup V = U$, which is impossible in models of ZFC such as $V$ itself.

Interestingly, $x$ is a subset of $V$ if, and only if, $x$ is a member of $V$. Therefore, we can consider what happens if the union condition is replaced with $x \in V \implies \cup x \in V$. In this case, there are no known contradictions, and any Grothendieck universe satisfies the new pair of properties. However, whether Grothendieck universes exist is a question beyond ZFC.

''V'' and the axiom of regularity

The formula ''V'' = ⋃_α''V''_α is often considered to be a theorem, not a definition. Roitman states (without references) that the realization that the axiom of regularity is equivalent to the equality of the universe of ZF sets to the cumulative hierarchy is due to von Neumann.. See page 79.

The existential status of ''V''

Since the class ''V'' may be considered to be the arena for most of mathematics, it is important to establish that it "exists" in some sense. Since existence is a difficult concept, one typically replaces the existence question with the consistency question, that is, whether the concept is free of contradictions. A major obstacle is posed by Gödel's incompleteness theorems, which effectively imply the impossibility of proving the consistency of ZF set theory in ZF set theory itself, provided that it is in fact consistent.

The integrity of the von Neumann universe depends fundamentally on the integrity of the ordinal numbers, which act as the rank parameter in the construction, and the integrity of transfinite induction, by which both the ordinal numbers and the von Neumann universe are constructed. The integrity of the ordinal number construction may be said to rest upon von Neumann's 1923 and 1928 papers. The integrity of the construction of ''V'' by transfinite induction may be said to have then been established in Zermelo's 1930 paper.

History

The cumulative type hierarchy, also known as the von Neumann universe, is claimed by Gregory H. Moore (1982) to be inaccurately attributed to von Neumann.. See page 279 for the assertion of the false attribution to von Neumann. See pages 270 and 281 for the attribution to Zermelo. The first publication of the von Neumann universe was by Ernst Zermelo in 1930.. See particularly pages 36–40.

Existence and uniqueness of the general transfinite recursive definition of sets was demonstrated in 1928 by von Neumann for both Zermelo-Fraenkel set theory and von Neumann's own set theory (which later developed into NBG set theory). In neither of these papers did he apply his transfinite recursive method to construct the universe of all sets. The presentations of the von Neumann universe by Bernays. See pages 203–209. and Mendelson. See page 202. both give credit to von Neumann for the transfinite induction construction method, although not for its application to the construction of the universe of ordinary sets.

The notation ''V'' is not a tribute to the name of von Neumann. It was used for the universe of sets in 1889 by Peano, the letter ''V'' signifying "Verum", which he used both as a logical symbol and to denote the class of all individuals.. See pages VIII and XI. Peano's notation ''V'' was adopted also by Whitehead and Russell for the class of all sets in 1910.. See page 229. The ''V'' notation (for the class of all sets) was not used by von Neumann in his 1920s papers about ordinal numbers and transfinite induction. Paul Cohen. See page 88. explicitly attributes his use of the letter ''V'' (for the class of all sets) to a 1940 paper by Gödel,. although Gödel most likely obtained the notation from earlier sources such as Whitehead and Russell.

Philosophical perspectives

There are two approaches to understanding the relationship of the von Neumann universe V to ZFC (along with many variations of each approach, and shadings between them). Roughly, formalists will tend to view V as something that flows from the ZFC axioms (for example, ZFC proves that every set is in V). On the other hand, realists are more likely to see the von Neumann hierarchy as something directly accessible to the intuition, and the axioms of ZFC as propositions for whose truth in V we can give direct intuitive arguments in natural language. A possible middle position is that the mental picture of the von Neumann hierarchy provides the ZFC axioms with a motivation (so that they are not arbitrary), but does not necessarily describe objects with real existence.

See also

* Universe (mathematics)
* Constructible universe
* Grothendieck universe
* Inaccessible cardinal
* S (set theory)

Notes

References

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* . English translation:
*
*
*
*

{{Mathematical logic

John von Neumann
Set-theoretic universes