Quasiperiodic function on:
[Wikipedia]
[Google]
[Amazon]
In 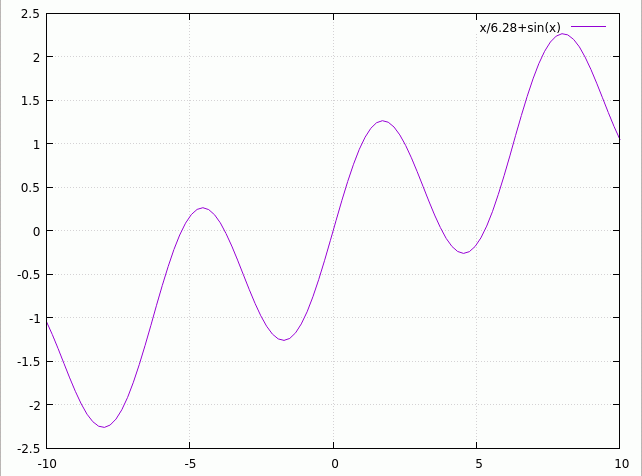 A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation:
:
Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation:
:
An example of this is the Jacobi theta function, where
:
shows that for fixed it has quasiperiod ; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or other periodic linear equations) can be found in quasiperiodic form, and a related form of quasi-periodic solution for periodic linear differential equations is expressed by Floquet theory.
Functions with an additive functional equation
:
are also called quasiperiodic. An example of this is the Weierstrass zeta function, where
:
for a ''z''-independent η when ω is a period of the corresponding Weierstrass ℘ function.
In the special case where we say ''f'' is periodic with period ω in the period lattice .
A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation:
:
Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation:
:
An example of this is the Jacobi theta function, where
:
shows that for fixed it has quasiperiod ; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or other periodic linear equations) can be found in quasiperiodic form, and a related form of quasi-periodic solution for periodic linear differential equations is expressed by Floquet theory.
Functions with an additive functional equation
:
are also called quasiperiodic. An example of this is the Weierstrass zeta function, where
:
for a ''z''-independent η when ω is a period of the corresponding Weierstrass ℘ function.
In the special case where we say ''f'' is periodic with period ω in the period lattice .
Quasiperiodic function
at
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a quasiperiodic function is a function that has a certain similarity to a periodic function
A periodic function, also called a periodic waveform (or simply periodic wave), is a function that repeats its values at regular intervals or periods. The repeatable part of the function or waveform is called a ''cycle''. For example, the t ...
. A function is quasiperiodic with quasiperiod if , where is a "''simpler''" function than . What it means to be "''simpler''" is vague.
 A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation:
:
Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation:
:
An example of this is the Jacobi theta function, where
:
shows that for fixed it has quasiperiod ; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or other periodic linear equations) can be found in quasiperiodic form, and a related form of quasi-periodic solution for periodic linear differential equations is expressed by Floquet theory.
Functions with an additive functional equation
:
are also called quasiperiodic. An example of this is the Weierstrass zeta function, where
:
for a ''z''-independent η when ω is a period of the corresponding Weierstrass ℘ function.
In the special case where we say ''f'' is periodic with period ω in the period lattice .
A simple case (sometimes called arithmetic quasiperiodic) is if the function obeys the equation:
:
Another case (sometimes called geometric quasiperiodic) is if the function obeys the equation:
:
An example of this is the Jacobi theta function, where
:
shows that for fixed it has quasiperiod ; it also is periodic with period one. Another example is provided by the Weierstrass sigma function, which is quasiperiodic in two independent quasiperiods, the periods of the corresponding Weierstrass ''℘'' function. Bloch's theorem says that the eigenfunctions of a periodic Schrödinger equation (or other periodic linear equations) can be found in quasiperiodic form, and a related form of quasi-periodic solution for periodic linear differential equations is expressed by Floquet theory.
Functions with an additive functional equation
:
are also called quasiperiodic. An example of this is the Weierstrass zeta function, where
:
for a ''z''-independent η when ω is a period of the corresponding Weierstrass ℘ function.
In the special case where we say ''f'' is periodic with period ω in the period lattice .
Quasiperiodic signals
Quasiperiodic signals in the sense of audio processing are not quasiperiodic functions in the sense defined here; instead they have the nature ofalmost periodic function
In mathematics, an almost periodic function is, loosely speaking, a function of a real variable that is periodic to within any desired level of accuracy, given suitably long, well-distributed "almost-periods". The concept was first studied by ...
s and that article should be consulted. The more vague and general notion of quasiperiodicity
Quasiperiodicity is the property of a system that displays irregular periodicity. Periodic behavior is defined as recurring at regular intervals, such as "every 24 hours". Quasiperiodic behavior is almost but not quite periodic. The term used to d ...
has even less to do with quasiperiodic functions in the mathematical sense.
A useful example is the function:
:
If the ratio is rational
Rationality is the quality of being guided by or based on reason. In this regard, a person acts rationally if they have a good reason for what they do, or a belief is rational if it is based on strong evidence. This quality can apply to an ...
, this will have a true period, but if is irrational
Irrationality is cognition, thinking, talking, or acting without rationality.
Irrationality often has a negative connotation, as thinking and actions that are less useful or more illogical than other more rational alternatives. The concept of ...
there is no true period, but a succession of increasingly accurate "almost" periods.
See also
* Quasiperiodic motionReferences
{{ReflistExternal links
Quasiperiodic function
at
PlanetMath
PlanetMath is a free content, free, collaborative, mathematics online encyclopedia. Intended to be comprehensive, the project is currently hosted by the University of Waterloo. The site is owned by a US-based nonprofit corporation, "PlanetMath.org ...
Complex analysis
Types of functions