Quasifibration

In algebraic topology, a quasifibration is a generalisation of fibre bundles and fibrations introduced by Albrecht Dold and René Thom. Roughly speaking, it is a continuous map ''p'': ''E'' → ''B'' having the same behaviour as a fibration regarding the (relative) homotopy groups of ''E'', ''B'' and ''p''⁻¹(''x''). Equivalently, one can define a quasifibration to be a continuous map such that the inclusion of each fibre into its homotopy fibre is a weak equivalence. One of the main applications of quasifibrations lies in proving the Dold-Thom theorem.

Definition

A continuous surjective map of topological spaces ''p'': ''E'' → ''B'' is called a quasifibration if it induces isomorphisms

: $p_*\colon \pi_i(E,p^(x),y) \to \pi_i(B,x)$

for all ''x'' ∈ ''B'', ''y'' ∈ ''p''⁻¹(''x'') and ''i'' ≥ 0. For ''i'' = 0,1 one can only speak of bijections between the two sets.

By definition, quasifibrations share a key property of fibrations, namely that a quasifibration ''p'': ''E'' → ''B'' induces a long exact sequence of homotopy groups

: $\begin \dots\to \pi_(B,x)\to \pi_i(p^(x),y)\to \pi_i(E,y)&\to \pi_i(B,x)\to \dots \\ &\to \pi_0(B,x)\to 0 \end$

as follows directly from the long exact sequence for the pair (''E'', ''p''⁻¹(''x'')).

This long exact sequence is also functorial in the following sense: Any fibrewise map ''f'': ''E'' → ''E′'' induces a morphism between the exact sequences of the pairs (''E'', ''p''⁻¹(''x'')) and (''E′'', ''p′''⁻¹(''x'')) and therefore a morphism between the exact sequences of a quasifibration. Hence, the diagram

commutes with ''f''₀ being the restriction of ''f'' to ''p''⁻¹(''x'') and ''x′'' being an element of the form ''p′''(''f''(''e'')) for an ''e'' ∈ ''p''⁻¹(''x'').

An equivalent definition is saying that a surjective map ''p'': ''E'' → ''B'' is a quasifibration if the inclusion of the fibre ''p''⁻¹(''b'') into the homotopy fibre ''F''_''b'' of ''p'' over ''b'' is a weak equivalence for all ''b'' ∈ ''B''. To see this, recall that ''F''_''b'' is the fibre of ''q'' under ''b'' where ''q'': ''E''_''p'' → ''B'' is the usual path fibration construction. Thus, one has

:$E_p=\$

and ''q'' is given by ''q''(''e'', γ) = γ(1). Now consider the natural homotopy equivalence φ : ''E'' → ''E''_''p'', given by φ(''e'') = (''e'', ''p''(''e'')), where ''p''(''e'') denotes the corresponding constant path. By definition, ''p'' factors through ''E''_''p'' such that one gets a commutative diagram

Applying π_''n'' yields the alternative definition.

Examples

* Every Serre fibration is a quasifibration. This follows from the Homotopy lifting property.
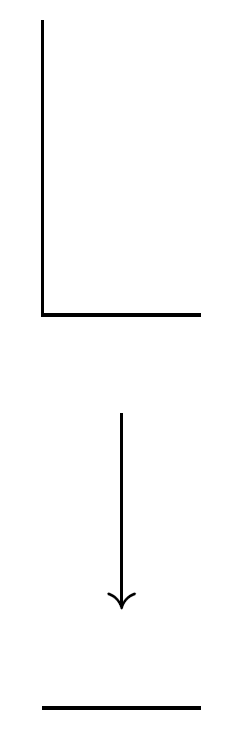
* The projection of the letter L onto its base interval is a quasifibration, but not a fibration. More generally, the projection ''M''_''f'' → ''I'' of the mapping cylinder of a map ''f'': ''X'' → ''Y'' between connected CW complexes onto the unit interval is a quasifibration if and only if π_''i''(''M''_''f'', ''p''⁻¹(''b'')) = 0 = π_''i''(''I'', ''b'') holds for all ''i'' ∈ ''I'' and ''b'' ∈ ''B''. But by the long exact sequence of the pair (''M''_''f'', ''p''⁻¹(''b'')) and by Whitehead's theorem, this is equivalent to ''f'' being a homotopy equivalence. For topological spaces ''X'' and ''Y'' in general, it is equivalent to ''f'' being a weak homotopy equivalence. Furthermore, if ''f'' is not surjective, non-constant paths in ''I'' starting at 0 cannot be lifted to paths starting at a point of ''Y'' outside the image of ''f'' in ''M''_''f''. This means that the projection is not a fibration in this case.
* The map SP(''p'') : SP(''X'') → SP(''X''/''A'') induced by the projection ''p'': ''X'' → ''X''/''A'' is a quasifibration for a CW pair (''X'', ''A'') consisting of two connected spaces. This is one of the main statements used in the proof of the Dold-Thom theorem. In general, this map also fails to be a fibration.

Properties

The following is a direct consequence of the alternative definition of a fibration using the homotopy fibre:

:Theorem. Every quasifibration ''p'': ''E'' → ''B'' factors through a fibration whose fibres are weakly homotopy equivalent to the ones of ''p''.

A corollary of this theorem is that all fibres of a quasifibration are weakly homotopy equivalent if the base space is path-connected, as this is the case for fibrations.

Checking whether a given map is a quasifibration tends to be quite tedious. The following two theorems are designed to make this problem easier. They will make use of the following notion: Let ''p'': ''E'' → ''B'' be a continuous map. A subset ''U'' ⊂ ''p''(''E'') is called distinguished (with respect to ''p'') if ''p'': ''p''⁻¹(''U'') → ''U'' is a quasifibration.

:Theorem. If the open subsets ''U,V'' and ''U'' ∩ ''V'' are distinguished with respect to the continuous map ''p'': ''E'' → ''B'', then so is ''U'' ∪ ''V''.Dold and Thom (1958), Satz 2.2

:Theorem. Let ''p'': ''E'' → ''B'' be a continuous map where ''B'' is the inductive limit of a sequence ''B''₁ ⊂ ''B''₂ ⊂ ... All ''B''_''n'' are moreover assumed to satisfy the first separation axiom. If all the ''B''_''n'' are distinguished, then ''p'' is a quasifibration.

To see that the latter statement holds, one only needs to bear in mind that continuous images of compact sets in ''B'' already lie in some ''B''_''n''. That way, one can reduce it to the case where the assertion is known.
These two theorems mean that it suffices to show that a given map is a quasifibration on certain subsets. Then one can patch these together in order to see that it holds on bigger subsets and finally, using a limiting argument, one sees that the map is a quasifibration on the whole space. This procedure has e.g. been used in the proof of the Dold-Thom theorem.

Notes

References

*
*
*
*
*
* {{cite book, last=Piccinini, first=Renzo A., title=Lectures on Homotopy Theory, publisher=Elsevier, isbn=9780080872827, year=1992

Further reading

Quasifibrations and homotopy pullbacks
on MathOverflow

Quasifibrations
from the Lehigh University
* http://pantodon.jp/index.rb?body=quasifibration in Japanese

Algebraic topology