Quadrisecant on:
[Wikipedia]
[Google]
[Amazon]
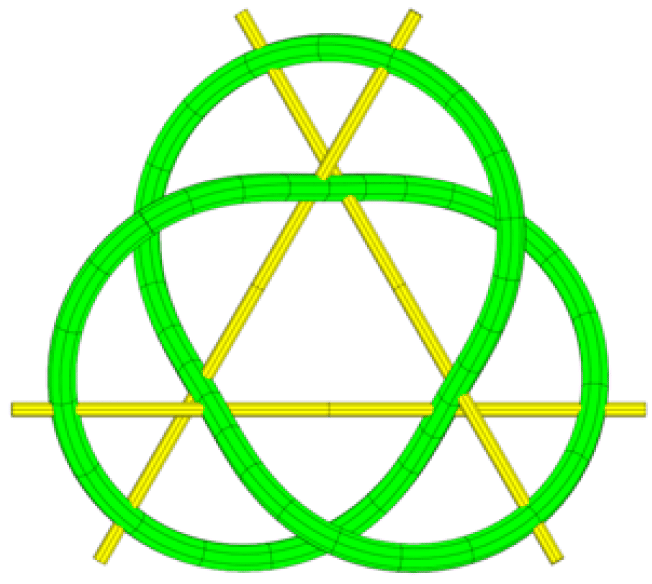 In
In
 In three-dimensional
In three-dimensional
 In
In geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, a quadrisecant or quadrisecant line of a space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
is a line that passes through four points of the curve. This is the largest possible number of intersections that a generic space curve can have with a line, and for such curves the quadrisecants form a discrete set of lines. Quadrisecants have been studied for curves of several types:
* Knots and links in knot theory
In topology, knot theory is the study of knot (mathematics), mathematical knots. While inspired by knots which appear in daily life, such as those in shoelaces and rope, a mathematical knot differs in that the ends are joined so it cannot be und ...
, when nontrivial
In mathematics, the adjective trivial is often used to refer to a claim or a case which can be readily obtained from context, or a particularly simple object possessing a given structure (e.g., group (mathematics), group, topological space). The n ...
, always have quadrisecants, and the existence and number of quadrisecants has been studied in connection with knot invariants including the minimum total curvature and the ropelength of a knot.
*The number of quadrisecants of a non-singular algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane cu ...
in complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a ...
can be computed by a formula derived by Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
He ...
.
*Quadrisecants of arrangements of skew lines
In three-dimensional geometry, skew lines are two Line (geometry), lines that do not Line-line intersection, intersect and are not Parallel (geometry), parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges ...
touch subsets of four lines from the arrangement. They are associated with ruled surface
In geometry, a Differential geometry of surfaces, surface in 3-dimensional Euclidean space is ruled (also called a scroll) if through every Point (geometry), point of , there is a straight line that lies on . Examples include the plane (mathemat ...
s and the Schläfli double six configuration.
Definition and motivation
A quadrisecant is a line that intersects a curve, surface, or other set in four distinct points. It is analogous to asecant line
In geometry, a secant is a line (geometry), line that intersects a curve at a minimum of two distinct Point (geometry), points..
The word ''secant'' comes from the Latin word ''secare'', meaning ''to cut''. In the case of a circle, a secant inter ...
, a line that intersects a curve or surface in two points; and a trisecant, a line that intersects a curve or surface in three points.
Compared to secants and trisecants, quadrisecants are especially relevant for space curve
In mathematics, a curve (also called a curved line in older texts) is an object similar to a line, but that does not have to be straight.
Intuitively, a curve may be thought of as the trace left by a moving point. This is the definition that ...
s, because they have the largest possible number of intersection points of a line with a generic curve. In the plane, a generic curve can be crossed arbitrarily many times by a line; for instance, small generic perturbations of the sine curve
A sine wave, sinusoidal wave, or sinusoid (symbol: ∿) is a periodic wave whose waveform (shape) is the trigonometric sine function. In mechanics, as a linear motion over time, this is '' simple harmonic motion''; as rotation, it correspon ...
are crossed infinitely often by the horizontal axis. In contrast, if an arbitrary space curve is perturbed by a small distance to make it generic, there will be no lines through five or more points of the perturbed curve. Nevertheless, any quadrisecants of the original space curve will remain present nearby in its perturbation. For generic space curves, the quadrisecants form a discrete set of lines. In contrast, when trisecants occur, they form continuous families of lines.
One explanation for this phenomenon is visual: looking at a space curve from far away, the space of such points of view can be described as a two-dimensional sphere, one point corresponding to each direction. Pairs of strands of the curve may appear to cross from all of these points of view, or from a two-dimensional subset of them. Three strands will form a triple crossing when the point of view lies on a trisecant, and four strands will form a quadruple crossing from a point of view on a quadrisecant. Each constraint that the crossing of a pair of strands lies on another strand reduces the number of degrees of freedom
In many scientific fields, the degrees of freedom of a system is the number of parameters of the system that may vary independently. For example, a point in the plane has two degrees of freedom for translation: its two coordinates; a non-infinite ...
by one (for a generic curve), so the points of view on trisecants form a one-dimensional (continuously infinite) subset of the sphere, while the points of view on quadrisecants form a zero-dimensional (discrete) subset. C. T. C. Wall writes that the fact that generic space curves are crossed at most four times by lines is "one of the simplest theorems of the kind", a model case for analogous theorems on higher-dimensional transversals.
Depending on the properties of the curve, it may have no quadrisecants, finitely many, or infinitely many. These considerations make it of interest to determine conditions for the existence of quadrisecants, or to find bounds on their number in various special cases, such as knotted curves, algebraic curves, or arrangements of lines.
For special classes of curves
Knots and links
In three-dimensionalEuclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, every nontrivial
In mathematics, the adjective trivial is often used to refer to a claim or a case which can be readily obtained from context, or a particularly simple object possessing a given structure (e.g., group (mathematics), group, topological space). The n ...
tame knot
A knot is an intentional complication in Rope, cordage which may be practical or decorative, or both. Practical knots are classified by function, including List of hitch knots, hitches, List of bend knots, bends, List of loop knots, loop knots, ...
or link has a quadrisecant. Originally established in the case of knotted polygon
In geometry, a polygon () is a plane figure made up of line segments connected to form a closed polygonal chain.
The segments of a closed polygonal chain are called its '' edges'' or ''sides''. The points where two edges meet are the polygon ...
s and smooth knots by Erika Pannwitz,
this result was extended to knots in suitably general position and links with nonzero linking number,
and later to all nontrivial tame knots and links.
Pannwitz proved more strongly that, for a locally flat disk having the knot as its boundary, the number of singularities of the disk can be used to construct a lower bound on the number of distinct quadrisecants. The existence of at least one quadrisecant follows from the fact that any such disk must have at least one singularity. conjectured that the number of distinct quadrisecants of a given knot is always at least , where is the crossing number of the knot. Counterexamples to this conjecture have since been discovered.
Two-component links have quadrisecants in which the points on the quadrisecant appear in alternating order between the two components, and nontrivial knots have quadrisecants in which the four points, ordered cyclically as on the knot, appear in order along the quadrisecant. The existence of these alternating quadrisecants can be used to derive the Fáry–Milnor theorem, a lower bound on the total curvature of a nontrivial knot. Quadrisecants have also been used to find lower bounds on the ropelength of knots.
G. T. Jin and H. S. Kim conjectured that, when a knotted curve has finitely many quadrisecants, can be approximated with an equivalent polygonal knot with its vertices at the points where the quadrisecants intersect , in the same order as they appear on . However, their conjecture is false: in fact, for every knot type, there is a realization for which this construction leads to a self-intersecting polygon, and another realization where this construction produces a knot of a different type.
It has been conjectured that every wild knot
In the mathematical theory of knots, a knot is tame if it can be "thickened", that is, if there exists an extension to an embedding of the solid torus S^1\times D^2 into the 3-sphere. A knot is tame if and only if it can be represented as a fin ...
has an infinite number of quadrisecants.
Algebraic curves
Arthur Cayley
Arthur Cayley (; 16 August 1821 – 26 January 1895) was a British mathematician who worked mostly on algebra. He helped found the modern British school of pure mathematics, and was a professor at Trinity College, Cambridge for 35 years.
He ...
derived a formula for the number of quadrisecants of an algebraic curve
In mathematics, an affine algebraic plane curve is the zero set of a polynomial in two variables. A projective algebraic plane curve is the zero set in a projective plane of a homogeneous polynomial in three variables. An affine algebraic plane cu ...
in three-dimensional complex projective space
In mathematics, complex projective space is the projective space with respect to the field of complex numbers. By analogy, whereas the points of a real projective space label the lines through the origin of a real Euclidean space, the points of a ...
, as a function of its degree and genus
Genus (; : genera ) is a taxonomic rank above species and below family (taxonomy), family as used in the biological classification of extant taxon, living and fossil organisms as well as Virus classification#ICTV classification, viruses. In bino ...
. For a curve of degree and genus , the number of quadrisecants is
This formula assumes that the given curve is non-singular; adjustments may be necessary if it has singular points.
Skew lines
Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are ''Euclidean spaces ...
, every set of four skew lines
In three-dimensional geometry, skew lines are two Line (geometry), lines that do not Line-line intersection, intersect and are not Parallel (geometry), parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges ...
in general position has either two quadrisecants (also in this context called transversals) or none. Any three of the four lines determine a hyperboloid
In geometry, a hyperboloid of revolution, sometimes called a circular hyperboloid, is the surface generated by rotating a hyperbola around one of its principal axes. A hyperboloid is the surface obtained from a hyperboloid of revolution by def ...
, a doubly ruled surface in which one of the two sets of ruled lines contains the three given lines, and the other ruling consists of trisecants to the given lines. If the fourth of the given lines pierces this surface, it has two points of intersection, because the hyperboloid is defined by a quadratic equation
In mathematics, a quadratic equation () is an equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where the variable (mathematics), variable represents an unknown number, and , , and represent known numbers, where . (If and ...
. The two trisecants of the ruled surface, through these two points, form two quadrisecants of the given four lines. On the other hand, if the fourth line is disjoint from the hyperboloid, then there are no quadrisecants. In spaces with complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
coordinates rather than real coordinates, four skew lines always have exactly two quadrisecants.
The quadrisecants of sets of lines play an important role in the construction of the Schläfli double six, a configuration
Configuration or configurations may refer to:
Computing
* Computer configuration or system configuration
* Configuration file, a software file used to configure the initial settings for a computer program
* Configurator, also known as choice board ...
of twelve lines intersecting each other in 30 crossings. If five lines are given in three-dimensional space, such that all five are intersected by a common line but are otherwise in general position, then each of the five quadruples of the lines has a second quadrisecant , and the five lines formed in this way are all intersected by a common line . These twelve lines and the 30 intersection points form the double six.
An arrangement of complex lines with a given number of pairwise intersections and otherwise skew may be interpreted as an algebraic curve with degree and with genus determined from its number of intersections, and Cayley's aforementioned formula used to count its quadrisecants. The same result as this formula can also be obtained by classifying the quadruples of lines by their intersections, counting the number of quadrisecants for each type of quadruple, and summing over all quadruples of lines in the given set.
References
{{reflist, refs= {{citation , last1 = Bai , first1 = Sheng , last2 = Wang , first2 = Chao , last3 = Wang , first3 = Jiajun , doi = 10.1142/S0218216518500220 , issue = 2 , journal = Journal of Knot Theory and Its Ramifications , mr = 3770471 , at = 1850022 , title = Counterexamples to the quadrisecant approximation conjecture , volume = 27 , year = 2018, arxiv = 1605.00538 , s2cid = 119601013 {{citation , last = Cayley , first = Arthur , author-link = Arthur Cayley , jstor = 108806 , pages = 453–483 , title =Philosophical Transactions of the Royal Society of London
''Philosophical Transactions of the Royal Society'' is a scientific journal published by the Royal Society. In its earliest days, it was a private venture of the Royal Society's secretary. It was established in 1665, making it the second journ ...
, volume = 153
, year = 1863, publisher = The Royal Society
{{citation
, last = Coxeter , first = H. S. M. , authorlink = Harold Scott MacDonald Coxeter
, contribution = An absolute property of four mutually tangent circles
, doi = 10.1007/0-387-29555-0_5
, location = New York
, mr = 2191243
, pages = 109–114
, publisher = Springer
, series = Math. Appl. (N. Y.)
, title = Non-Euclidean geometries
, volume = 581
, year = 2006; Coxeter repeats Schläfli's construction, and provides several references to simplified proofs of its correctness
{{citation
, last = Denne , first = Elizabeth Jane
, arxiv = math/0510561
, publisher = University of Illinois at Urbana-Champaign
The University of Illinois Urbana-Champaign (UIUC, U of I, Illinois, or University of Illinois) is a public land-grant research university in the Champaign–Urbana metropolitan area, Illinois, United States. Established in 1867, it is the f ...
, series = Ph.D. thesis
, title = Alternating quadrisecants of knots
, year = 2004, bibcode = 2005math.....10561D
{{citation
, last = Denne , first = Elizabeth
, editor1-last = Blatt , editor1-first = Simon
, editor2-last = Reiter , editor2-first = Philipp
, editor3-last = Schikorra , editor3-first = Armin
, contribution = Quadrisecants and essential secants of knots
, doi = 10.1515/9783110571493-006
, mr = 3915943
, pages = 138–158
, publisher = De Gruyter, Berlin
, series = Partial Differential Equations and Measure Theory
, title = New directions in geometric and applied knot theory
, year = 2018, s2cid = 128222971
, doi-access = free
{{citation
, last1 = Denne , first1 = Elizabeth
, last2 = Diao , first2 = Yuanan
, last3 = Sullivan , first3 = John M. , author3-link = John M. Sullivan (mathematician)
, doi = 10.2140/gt.2006.10.1
, journal = Geometry & Topology
, mr = 2207788
, pages = 1–26
, title = Quadrisecants give new lower bounds for the ropelength of a knot
, url = http://msp.warwick.ac.uk/gt/2006/10/p001.xhtml
, volume = 10
, year = 2006, arxiv = math/0408026, s2cid = 5770206
{{citation
, last1 = Eisenbud , first1 = David , author1-link = David Eisenbud
, last2 = Harris , first2 = Joe , author2-link = Joe Harris (mathematician)
, doi = 10.1017/CBO9781139062046
, isbn = 978-1-107-60272-4
, mr = 3617981
, page = 377
, publisher = Cambridge University Press , location = Cambridge, UK
, title = 3264 and All That: A second course in algebraic geometry
, url = https://books.google.com/books?id=au67CwAAQBAJ&pg=PA377
, year = 2016
{{citation
, last1 = Griffiths , first1 = Phillip
, last2 = Harris , first2 = Joseph
, isbn = 9781118030776
, page = 296
, publisher = John Wiley & Sons
, series = Wiley Classics Library
, title = Principles of Algebraic Geometry
, url = https://books.google.com/books?id=Sny48qKdW40C&pg=PA296
, volume = 52
, year = 2011
{{citation
, last1 = Hilbert , first1 = David , author1-link = David Hilbert
, last2 = Cohn-Vossen , first2 = Stephan , author2-link = Stephan Cohn-Vossen
, location = New York
, page = 164
, publisher = Chelsea
, title = Geometry and the Imagination
, year = 1952; reprinted 1990, {{isbn, 978-0-8284-1087-8
{{citation
, last = Jin , first = Gyo Taek
, contribution = Quadrisecants of knots with small crossing number
, doi = 10.1142/9789812703460_0025
, mr = 2197955
, pages = 507–523
, publisher = World Scientific Publishing , location = Singapore
, series = Ser. Knots Everything
, title = Physical and numerical models in knot theory
, url = https://mathsci.kaist.ac.kr/~jin/papers/quad-small-xing/quad-small-xing.pdf
, volume = 36
, year = 2005
{{citation
, last = Jin , first = Gyo Taek
, editor1-last = Reiter , editor1-first = Philipp
, editor2-last = Blatt , editor2-first = Simon
, editor3-last = Schikorra , editor3-first = Armin
, contribution = Polygonal approximation of unknots by quadrisecants
, date = December 2017
, doi = 10.1515/9783110571493-008
, pages = 159–175
, publisher = De Gruyter Open
, title = New Directions in Geometric and Applied Knot Theory, doi-access = free
{{citation
, last = Kuperberg , first = Greg , author-link = Greg Kuperberg
, arxiv = math/9712205
, doi = 10.1142/S021821659400006X
, journal = Journal of Knot Theory and Its Ramifications
, mr = 1265452
, pages = 41–50
, title = Quadrisecants of knots and links
, volume = 3
, year = 1994, s2cid = 6103528
{{citation
, last1 = Maxwell , first1 = Edwin A. , authorlink1=Edwin A. Maxwell
, date = July 1935
, doi = 10.1017/s0305004100013086
, issue = 3
, journal = Mathematical Proceedings of the Cambridge Philosophical Society
, pages = 324–326
, title = Note on the formula for the number of quadrisecants of a curve in space of three dimensions
, volume = 31, s2cid = 122279811
{{citation
, last1 = Morton , first1 = Hugh R.
, last2 = Mond , first2 = David M. Q.
, doi = 10.1016/0040-9383(82)90007-6
, journal = Topology
Topology (from the Greek language, Greek words , and ) is the branch of mathematics concerned with the properties of a Mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformat ...
, mr = 0649756
, pages = 235–243
, title = Closed curves with no quadrisecants
, volume = 21
, year = 1982, issue = 3
, doi-access = free
{{citation
, last = Pannwitz , first = Erika , author-link = Erika Pannwitz
, doi = 10.1007/BF01452857
, issue = 1
, journal = Mathematische Annalen
''Mathematische Annalen'' (abbreviated as ''Math. Ann.'' or, formerly, ''Math. Annal.'') is a German mathematical research journal founded in 1868 by Alfred Clebsch and Carl Neumann. Subsequent managing editors were Felix Klein, David Hilbert, ...
, pages = 629–672
, title = Eine elementargeometrische Eigenschaft von Verschlingungen und Knoten
, volume = 108
, year = 1933, s2cid = 123026724
{{citation
, last = Schläfli , first = Ludwig , authorlink = Ludwig Schläfli
, editor-last = Cayley , editor-first = Arthur , editor-link = Arthur Cayley
, journal = Quarterly Journal of Pure and Applied Mathematics
, pages = 55–65, 110–120
, title = An attempt to determine the twenty-seven lines upon a surface of the third order, and to derive such surfaces in species, in reference to the reality of the lines upon the surface
, url = http://resolver.sub.uni-goettingen.de/purl?PPN600494829_0002
, volume = 2
, year = 1858
{{citation
, last = Wall , first = C. T. C. , author-link = C. T. C. Wall
, editor1-last = Palis , editor1-first = Jacob
, editor2-last = do Carmo , editor2-first = Manfredo
, contribution = Geometric properties of generic differentiable manifolds
, doi = 10.1007/BFb0085382
, mr = 0494233
, pages = 707–774
, series = Lecture Notes in Mathematics
, title = Geometry and Topology: Proceedings of the Latin American School of Mathematics (ELAM III) held at the Instituto de Matemática Pura e Aplicada (IMPA), Rio de Janeiro, July 1976
, volume = 597
, year = 1977
{{citation
, last = Welchman , first = W. G.
, date = April 1932
, doi = 10.1017/s0305004100010872
, issue = 2
, journal = Mathematical Proceedings of the Cambridge Philosophical Society
, pages = 206–208
, title = Note on the trisecants and quadrisecants of a space curve
, volume = 28, s2cid = 120725025
{{citation
, last = Wong , first = B. C.
, doi = 10.1090/S0002-9904-1934-05854-3
, issue = 4
, journal = Bulletin of the American Mathematical Society
, mr = 1562839
, pages = 291–296
, title = Enumerative properties of -space curves
, volume = 40
, year = 1934, doi-access = free
Knot theory
Algebraic geometry