Pseudopotential

In physics, a pseudopotential or effective potential is used as an approximation for the simplified description of complex systems. Applications include atomic physics and neutron scattering. The pseudopotential approximation was first introduced by Hans Hellmann in 1934.

Atomic physics

The pseudopotential is an attempt to replace the complicated effects of the motion of the core (i.e. non-valence) electrons of an atom and its nucleus with an effective potential, or pseudopotential, so that the Schrödinger equation contains a modified effective potential term instead of the Coulombic potential term for core electrons normally found in the Schrödinger equation.

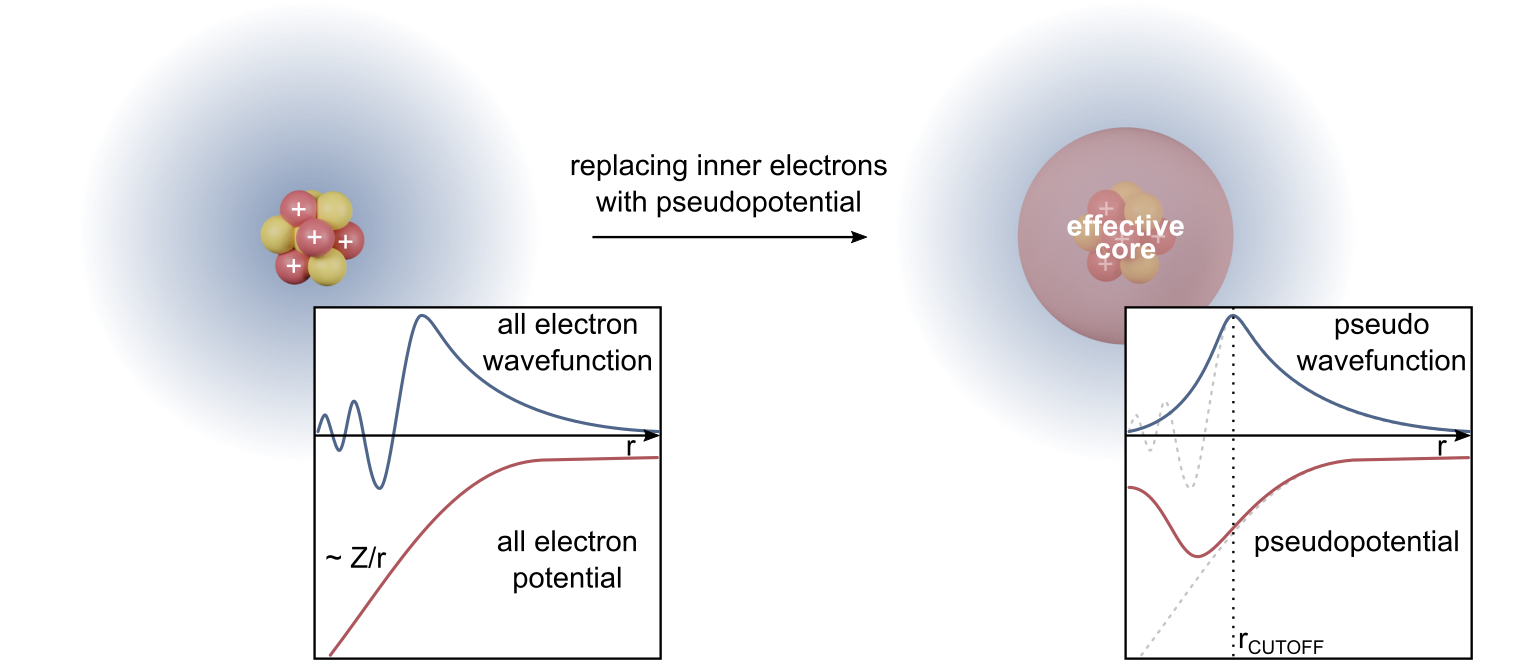
The pseudopotential is an effective potential constructed to replace the atomic all-electron potential (full-potential) such that core states are eliminated ''and'' the valence electrons are described by pseudo-wavefunctions with significantly fewer nodes. This allows the pseudo-wavefunctions to be described with far fewer Fourier modes, thus making plane-wave basis sets practical to use. In this approach usually only the chemically active valence electrons are dealt with explicitly, while the core electrons are 'frozen', being considered together with the nuclei as rigid non-polarizable ion cores. It is possible to self-consistently update the pseudopotential with the chemical environment that it is embedded in, having the effect of relaxing the frozen core approximation, although this is rarely done. In codes using local basis functions, like Gaussian, often effective core potentials are used that only freeze the core electrons.

First-principles pseudopotentials are derived from an atomic reference state, requiring that the pseudo- and all-electron valence eigenstates have the same energies and amplitude (and thus density) outside a chosen core cut-off radius $r_c$.

Pseudopotentials with larger cut-off radius are said to be ''softer'', that is more rapidly convergent, but at the same time less ''transferable'', that is less accurate to reproduce realistic features in different environments.

Motivation:
# Reduction of basis set size
# Reduction of number of electrons
# Inclusion of relativistic and other effects

Approximations:
# One-electron picture.
# The small-core approximation assumes that there is no significant overlap between core and valence wave-function. Nonlinear core corrections or "semicore" electron inclusion deal with situations where overlap is non-negligible.

Early applications of pseudopotentials to atoms and solids based on attempts to fit atomic spectra achieved only limited success. Solid-state pseudopotentials achieved their present popularity largely because of the successful fits by Walter Harrison to the nearly free electron Fermi surface of aluminum (1958) and by James C. Phillips to the covalent energy gaps of silicon and germanium (1958). Phillips and coworkers (notably Marvin L. Cohen and coworkers) later extended this work to many other semiconductors, in what they called "semiempirical pseudopotentials".

Norm-conserving pseudopotential

''Norm-conserving'' and ''ultrasoft'' are the two most common forms of pseudopotential used in modern plane-wave electronic structure codes. They allow a basis-set with a significantly lower cut-off (the frequency of the highest Fourier mode) to be used to describe the electron wavefunctions and so allow proper numerical convergence with reasonable computing resources. An alternative would be to augment the basis set around nuclei with atomic-like functions, as is done in LAPW. Norm-conserving pseudopotential was first proposed by Hamann, Schlüter, and Chiang (HSC) in 1979. The original HSC norm-conserving pseudopotential takes the following form:

:$\hat_(r) = \sum_l \sum_m , Y_ \rangle V_(r) \langle Y_ ,$

where $, Y_\rangle$ projects a one-particle wavefunction, such as one Kohn-Sham orbital, to the angular momentum labeled by $\$. $V_(r)$ is the pseudopotential that acts on the projected component. Different angular momentum states then feel different potentials, thus the HSC norm-conserving pseudopotential is non-local, in contrast to local pseudopotential which acts on all one-particle wave-functions in the same way.

Norm-conserving pseudopotentials are constructed to enforce two conditions.

1. Inside the cut-off radius $r_c$, the norm of each pseudo-wavefunction be identical to its corresponding all-electron wavefunction:

:$\int_ dr^3 \phi_(\vec r) \phi_ (\vec r) = \int_ dr^3 \tilde_ (\vec r) \tilde_ (\vec r)$,
:where $\phi_$ and $\tilde_$ are the all-electron and pseudo reference states for the pseudopotential on atom $\mathbf$.
2. All-electron and pseudo wavefunctions are identical outside cut-off radius $r_c$.

Ultrasoft pseudopotentials

Ultrasoft pseudopotentials relax the norm-conserving constraint to reduce the necessary basis-set size further at the expense of introducing a generalized eigenvalue problem. With a non-zero difference in norms we can now define:

:$q_ = \langle \phi_ , \phi_ \rangle - \langle \tilde_ , \tilde_ \rangle$,

and so a normalised eigenstate of the pseudo Hamiltonian now obeys the generalized equation

:$\hat , \Psi_i \rangle = \epsilon_i \hat , \Psi_i \rangle$,

where the operator $\hat$ is defined as

:$\hat = 1 + \sum_ , p_ \rangle q_ \langle p_ ,$,

where $p_$ are projectors that form a dual basis with the pseudo reference states inside the cut-off radius, and are zero outside:

:$\langle p_ , \tilde_ \rangle_ = \delta_$.

A related technique is the projector augmented wave (PAW) method.

Fermi pseudopotential

Enrico Fermi introduced a pseudopotential, $V$, to describe the scattering of a free neutron by a nucleus. The scattering is assumed to be ''s''-wave scattering, and therefore spherically symmetric. Therefore, the potential is given as a function of radius, $r$:

:$V(r)=\fracb\,\delta(r)$,

where $\hbar$ is the Planck constant divided by $2\pi$, $m$ is the mass, $\delta(r)$ is the Dirac delta function, $b$ is the bound coherent neutron scattering length, and $r=0$ the center of mass of the nucleus. The Fourier transform of this $\delta$-function leads to the constant neutron form factor.

Phillips pseudopotential

James Charles Phillips developed a simplified pseudopotential while at Bell Labs useful for describing silicon and germanium.

See also

* Density functional theory
* Projector augmented wave method
* Marvin L. Cohen
* Alex Zunger

References

Pseudopotential libraries

Pseudopotential Library
: A community website for pseudopotentials/effective core potentials developed for high accuracy correlated many-body methods such as quantum Monte Carlo and quantum chemistry


: This webpage maintained by th

provides a searchable database of pseudopotentials for density functional codes as well as links to pseudopotential generators, converters, and other online databases.

Vanderbilt Ultra-Soft Pseudopotential Site
: Website of David Vanderbilt with links to codes that implement ultrasoft pseudopotentials and libraries of generated pseudopotentials.

GBRV pseudopotential site
: This site hosts the GBRV pseudopotential library

PseudoDojo
: This site collates tested pseudo potentials sorted by type, accuracy, and efficiency, shows information on convergence of various tested properties and provides download options.

SSSP
: Standard Solid State Pseudopotentials

Further reading

*
*
*
*
*
*
*
* {{Citation , last1=Lejaeghere, first1=K., last2=Bihlmayer, first2=G., last3=Bjorkman, first3=T., last4=Blaha, first4=P., last5=Blugel, first5=S., last6=Blum, first6=V., last7=Caliste, first7=D., last8=Castelli, first8=I. E., last9=Clark, first9=S. J., last10=Dal Corso, first10=A., last11=de Gironcoli, first11=S., last12=Deutsch, first12=T., last13=Dewhurst, first13=J. K., last14=Di Marco, first14=I., last15=Draxl, first15=C., last16=Du ak, first16=M., last17=Eriksson, first17=O., last18=Flores-Livas, first18=J. A., last19=Garrity, first19=K. F., last20=Genovese, first20=L., last21=Giannozzi, first21=P., last22=Giantomassi, first22=M., last23=Goedecker, first23=S., last24=Gonze, first24=X., last25=Granas, first25=O., last26=Gross, first26=E. K. U., last27=Gulans, first27=A., last28=Gygi, first28=F., last29=Hamann, first29=D. R., last30=Hasnip, first30=P. J., last31=Holzwarth, first31=N. A. W., last32=Iu an, first32=D., last33=Jochym, first33=D. B., last34=Jollet, first34=F., last35=Jones, first35=D., last36=Kresse, first36=G., last37=Koepernik, first37=K., last38=Kucukbenli, first38=E., last39=Kvashnin, first39=Y. O., last40=Locht, first40=I. L. M., last41=Lubeck, first41=S., last42=Marsman, first42=M., last43=Marzari, first43=N., last44=Nitzsche, first44=U., last45=Nordstrom, first45=L., last46=Ozaki, first46=T., last47=Paulatto, first47=L., last48=Pickard, first48=C. J., last49=Poelmans, first49=W., last50=Probert, first50=M. I. J., last51=Refson, first51=K., last52=Richter, first52=M., last53=Rignanese, first53=G.-M., last54=Saha, first54=S., last55=Scheffler, first55=M., last56=Schlipf, first56=M., last57=Schwarz, first57=K., last58=Sharma, first58=S., last59=Tavazza, first59=F., last60=Thunstrom, first60=P., last61=Tkatchenko, first61=A., last62=Torrent, first62=M., last63=Vanderbilt, first63=D., last64=van Setten, first64=M. J., last65=Van Speybroeck, first65=V., last66=Wills, first66=J. M., last67=Yates, first67=J. R., last68=Zhang, first68=G.-X., last69=Cottenier, first69=S., title=Reproducibility in density functional theory calculations of solids, journal=Science, volume=351, issue=6280, year=2016, pages=aad3000, issn=0036-8075, doi=10.1126/science.aad3000, pmid=27013736, bibcode=2016Sci...351.....L, doi-access=free

Computational physics
Electronic structure methods
Quantum mechanical potentials