Point Location on:
[Wikipedia]
[Google]
[Amazon]
The point location problem is a fundamental topic of computational geometry. It finds applications in areas that deal with processing geometrical data:
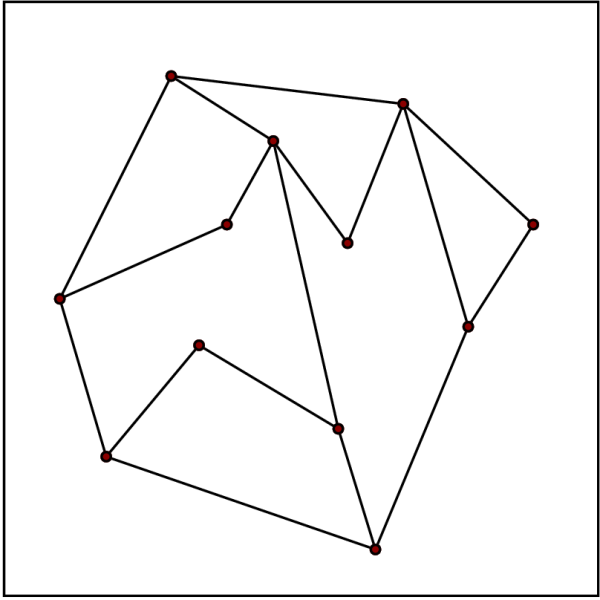 In the planar case, we are given a planar subdivision ''S'', formed by multiple
In the planar case, we are given a planar subdivision ''S'', formed by multiple
 The simplest and earliest data structure to achieve O(log ''n'') time was discovered by Dobkin and Lipton in 1976. It is based on subdividing ''S'' using vertical lines that pass through each vertex in ''S''. The region between two consecutive vertical lines is called a slab. Notice that each slab is divided by non-intersecting line segments that completely cross the slab from left to right. The region between two consecutive segments inside a slab corresponds to a unique face of ''S''. Therefore, we reduce our point location problem to two simpler problems:
# Given a subdivision of the plane into vertical slabs, determine which slab contains a given point.
# Given a slab subdivided into regions by non-intersecting segments that completely cross the slab from left to right, determine which region contains a given point.
The first problem can be solved by
The simplest and earliest data structure to achieve O(log ''n'') time was discovered by Dobkin and Lipton in 1976. It is based on subdividing ''S'' using vertical lines that pass through each vertex in ''S''. The region between two consecutive vertical lines is called a slab. Notice that each slab is divided by non-intersecting line segments that completely cross the slab from left to right. The region between two consecutive segments inside a slab corresponds to a unique face of ''S''. Therefore, we reduce our point location problem to two simpler problems:
# Given a subdivision of the plane into vertical slabs, determine which slab contains a given point.
# Given a slab subdivided into regions by non-intersecting segments that completely cross the slab from left to right, determine which region contains a given point.
The first problem can be solved by
 A (vertical) monotone chain is a path such that the ''y''-coordinate never increases along the path. A simple polygon is (vertical) monotone if it is formed by two monotone chains, with the first and last vertices in common. It is possible to add some edges to a planar subdivision, in order to make all faces monotone, obtaining what is called a monotone subdivision. This process does not add any vertices to the subdivision (therefore, the size remains O(''n'')), and can be performed in O(''n'' log ''n'') time by plane sweep (it can also be performed in linear time, using
A (vertical) monotone chain is a path such that the ''y''-coordinate never increases along the path. A simple polygon is (vertical) monotone if it is formed by two monotone chains, with the first and last vertices in common. It is possible to add some edges to a planar subdivision, in order to make all faces monotone, obtaining what is called a monotone subdivision. This process does not add any vertices to the subdivision (therefore, the size remains O(''n'')), and can be performed in O(''n'' log ''n'') time by plane sweep (it can also be performed in linear time, using
 A polygon with ''m'' vertices can be partitioned into ''m''–2 triangles. Which can be shown by induction starting from a triangle. There are numerous algorithms to triangulate a polygon efficiently, the fastest having O(''n'') worst case time. Therefore, we can decompose each polygon of our subdivision in triangles, and restrict our data structure to the case of subdivisions formed exclusively by triangles. Kirkpatrick gives a data structure for point location in triangulated subdivisions with O(''n'') storage space and O(log ''n'') query time.
The general idea is to build a hierarchy of triangles. To perform a query, we start by finding the top-level triangle that contains the query point. Since the number of top-level triangles is bounded by a constant, this operation can be performed in O(1) time. Each triangle has pointers to the triangles it intersects in the next level of the hierarchy, and the number of pointers is also bounded by a constant. We proceed with the query by finding which triangle contains the query point level by level.
The data structure is built in the opposite order, that is, bottom-up. We start with the triangulated subdivision, and choose an independent set of vertices to be removed. After removing the vertices, we retriangulate the subdivision. Because the subdivision is formed by triangles, a greedy algorithm can find an independent set that contains a constant fraction of the vertices. Therefore, the number of removal steps is O(log ''n'').
A polygon with ''m'' vertices can be partitioned into ''m''–2 triangles. Which can be shown by induction starting from a triangle. There are numerous algorithms to triangulate a polygon efficiently, the fastest having O(''n'') worst case time. Therefore, we can decompose each polygon of our subdivision in triangles, and restrict our data structure to the case of subdivisions formed exclusively by triangles. Kirkpatrick gives a data structure for point location in triangulated subdivisions with O(''n'') storage space and O(log ''n'') query time.
The general idea is to build a hierarchy of triangles. To perform a query, we start by finding the top-level triangle that contains the query point. Since the number of top-level triangles is bounded by a constant, this operation can be performed in O(1) time. Each triangle has pointers to the triangles it intersects in the next level of the hierarchy, and the number of pointers is also bounded by a constant. We proceed with the query by finding which triangle contains the query point level by level.
The data structure is built in the opposite order, that is, bottom-up. We start with the triangulated subdivision, and choose an independent set of vertices to be removed. After removing the vertices, we retriangulate the subdivision. Because the subdivision is formed by triangles, a greedy algorithm can find an independent set that contains a constant fraction of the vertices. Therefore, the number of removal steps is O(log ''n'').
 A
A
Point-Location Source Repository
at Stony Brook University
in
computer graphics
Computer graphics deals with generating images with the aid of computers. Today, computer graphics is a core technology in digital photography, film, video games, cell phone and computer displays, and many specialized applications. A great deal ...
, geographic information system
A geographic information system (GIS) is a type of database containing geographic data (that is, descriptions of phenomena for which location is relevant), combined with software tools for managing, analyzing, and visualizing those data. In a ...
s (GIS), motion planning
Motion planning, also path planning (also known as the navigation problem or the piano mover's problem) is a computational problem to find a sequence of valid configurations that moves the object from the source to destination. The term is used ...
, and computer aided design
Computer-aided design (CAD) is the use of computers (or ) to aid in the creation, modification, analysis, or optimization of a design. This software is used to increase the productivity of the designer, improve the quality of design, improve c ...
(CAD).
In its most general form, the problem is, given a partition of the space into disjoint regions, to determine the region where a query point lies. As an example application, each time one clicks a mouse to follow a link in a web browser
A web browser is application software for accessing websites. When a user requests a web page from a particular website, the browser retrieves its files from a web server and then displays the page on the user's screen. Browsers are used on ...
, this problem must be solved in order to determine which area of the computer screen is under the mouse pointer. A simple special case is the point in polygon problem. In this case, one needs to determine whether the point is inside, outside, or on the boundary of a single polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...
.
In many applications, one needs to determine the location of several different points with respect to the same partition of the space. To solve this problem efficiently, it is useful to build a data structure
In computer science, a data structure is a data organization, management, and storage format that is usually chosen for Efficiency, efficient Data access, access to data. More precisely, a data structure is a collection of data values, the rel ...
that, given a query point, quickly determines which region contains the query point (e.g. Voronoi Diagram).
Planar case
 In the planar case, we are given a planar subdivision ''S'', formed by multiple
In the planar case, we are given a planar subdivision ''S'', formed by multiple polygon
In geometry, a polygon () is a plane figure that is described by a finite number of straight line segments connected to form a closed '' polygonal chain'' (or ''polygonal circuit''). The bounded plane region, the bounding circuit, or the two t ...
s called faces, and need to determine which face contains a query point. A brute force search of each face using the point-in-polygon
In computational geometry, the point-in-polygon (PIP) problem asks whether a given point in the plane lies inside, outside, or on the boundary of a polygon. It is a special case of point location problems and finds applications in areas that deal ...
algorithm is possible, but usually not feasible for subdivisions of high complexity. Several different approaches lead to optimal data structures, with O(''n'') storage space and O(log ''n'') query time, where ''n'' is the total number of vertices in ''S''. For simplicity, we assume that the planar subdivision is contained inside a square bounding box.
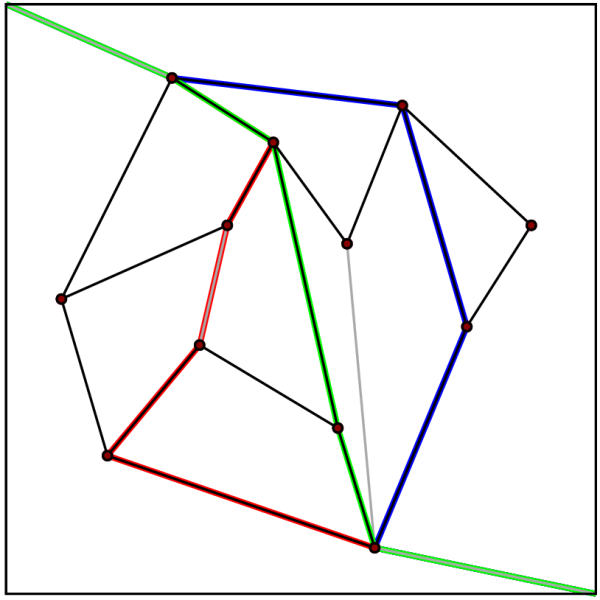
Slab decomposition
 The simplest and earliest data structure to achieve O(log ''n'') time was discovered by Dobkin and Lipton in 1976. It is based on subdividing ''S'' using vertical lines that pass through each vertex in ''S''. The region between two consecutive vertical lines is called a slab. Notice that each slab is divided by non-intersecting line segments that completely cross the slab from left to right. The region between two consecutive segments inside a slab corresponds to a unique face of ''S''. Therefore, we reduce our point location problem to two simpler problems:
# Given a subdivision of the plane into vertical slabs, determine which slab contains a given point.
# Given a slab subdivided into regions by non-intersecting segments that completely cross the slab from left to right, determine which region contains a given point.
The first problem can be solved by
The simplest and earliest data structure to achieve O(log ''n'') time was discovered by Dobkin and Lipton in 1976. It is based on subdividing ''S'' using vertical lines that pass through each vertex in ''S''. The region between two consecutive vertical lines is called a slab. Notice that each slab is divided by non-intersecting line segments that completely cross the slab from left to right. The region between two consecutive segments inside a slab corresponds to a unique face of ''S''. Therefore, we reduce our point location problem to two simpler problems:
# Given a subdivision of the plane into vertical slabs, determine which slab contains a given point.
# Given a slab subdivided into regions by non-intersecting segments that completely cross the slab from left to right, determine which region contains a given point.
The first problem can be solved by binary search
In computer science, binary search, also known as half-interval search, logarithmic search, or binary chop, is a search algorithm that finds the position of a target value within a sorted array. Binary search compares the target value to the m ...
on the ''x'' coordinate of the vertical lines in O(log ''n'') time. The second problem can also be solved in O(log ''n'') time by binary search. To see how, notice that, as the segments do not intersect and completely cross the slab, the segments can be sorted vertically inside each slab.
While this algorithm allows point location in logarithmic time and is easy to implement, the space required to build the slabs and the regions contained within the slabs can be as high as O(''n''²), since each slab can cross a significant fraction of the segments.
Several authors noticed that the segments that cross two adjacent slabs are mostly the same. Therefore, the size of the data structure can be significantly reduced. More specifically, Sarnak and Tarjan sweep a vertical line ''l'' from left to right over the plane, while maintaining the segments that intersect ''l'' in a Persistent red-black tree Red-black or Redblack may refer to:
* Ottawa Redblacks, a Canadian football team
* RED/BLACK concept, a concept in cryptography
* Red-black striped snake, a colubrid snake
* Red–black tree, a type of self-balancing binary search tree used in com ...
. This allows them to reduce the storage space to O(''n''), while maintaining the O(log ''n'') query time.
Monotone subdivisions
 A (vertical) monotone chain is a path such that the ''y''-coordinate never increases along the path. A simple polygon is (vertical) monotone if it is formed by two monotone chains, with the first and last vertices in common. It is possible to add some edges to a planar subdivision, in order to make all faces monotone, obtaining what is called a monotone subdivision. This process does not add any vertices to the subdivision (therefore, the size remains O(''n'')), and can be performed in O(''n'' log ''n'') time by plane sweep (it can also be performed in linear time, using
A (vertical) monotone chain is a path such that the ''y''-coordinate never increases along the path. A simple polygon is (vertical) monotone if it is formed by two monotone chains, with the first and last vertices in common. It is possible to add some edges to a planar subdivision, in order to make all faces monotone, obtaining what is called a monotone subdivision. This process does not add any vertices to the subdivision (therefore, the size remains O(''n'')), and can be performed in O(''n'' log ''n'') time by plane sweep (it can also be performed in linear time, using polygon triangulation
In computational geometry, polygon triangulation is the partition of a polygonal area ( simple polygon) into a set of triangles, i.e., finding a set of triangles with pairwise non-intersecting interiors whose union is .
Triangulations may ...
). Therefore, there is no loss of generality, if we restrict our data structure to the case of monotone subdivisions, as we do in this section.
The weakness of the slab decomposition is that the vertical lines create additional segments in the decomposition, making it difficult to achieve O(''n'') storage space. Edelsbrunner, Guibas, and Stolfi discovered an optimal data structure that only uses the edges in a monotone subdivision. The idea is to use vertical monotone chains, instead of using vertical lines to partition the subdivision.
Converting this general idea to an actual efficient data structure is not a simple task. First, we need to be able to compute a monotone chain that divides the subdivision into two halves of similar sizes. Second, since some edges may be contained in several monotone chains, we need to be careful to guarantee that the storage space is O(n). Third, testing whether a point is on the left or the right side of a monotone subdivision takes O(''n'') time if performed naïvely.
Details on how to solve the first two issues are beyond the scope of this article. We briefly mention how to address the third issue. Using binary search, we can test whether a point is to the left or right of a monotone chain in O(log ''n'') time. As we need to perform another nested binary search through O(log ''n'') chains to actually determine the point location, the query time is O(log² n). To achieve O(log ''n'') query time, we need to use fractional cascading, keeping pointers between the edges of different monotone chains.
Triangulation refinement
 A polygon with ''m'' vertices can be partitioned into ''m''–2 triangles. Which can be shown by induction starting from a triangle. There are numerous algorithms to triangulate a polygon efficiently, the fastest having O(''n'') worst case time. Therefore, we can decompose each polygon of our subdivision in triangles, and restrict our data structure to the case of subdivisions formed exclusively by triangles. Kirkpatrick gives a data structure for point location in triangulated subdivisions with O(''n'') storage space and O(log ''n'') query time.
The general idea is to build a hierarchy of triangles. To perform a query, we start by finding the top-level triangle that contains the query point. Since the number of top-level triangles is bounded by a constant, this operation can be performed in O(1) time. Each triangle has pointers to the triangles it intersects in the next level of the hierarchy, and the number of pointers is also bounded by a constant. We proceed with the query by finding which triangle contains the query point level by level.
The data structure is built in the opposite order, that is, bottom-up. We start with the triangulated subdivision, and choose an independent set of vertices to be removed. After removing the vertices, we retriangulate the subdivision. Because the subdivision is formed by triangles, a greedy algorithm can find an independent set that contains a constant fraction of the vertices. Therefore, the number of removal steps is O(log ''n'').
A polygon with ''m'' vertices can be partitioned into ''m''–2 triangles. Which can be shown by induction starting from a triangle. There are numerous algorithms to triangulate a polygon efficiently, the fastest having O(''n'') worst case time. Therefore, we can decompose each polygon of our subdivision in triangles, and restrict our data structure to the case of subdivisions formed exclusively by triangles. Kirkpatrick gives a data structure for point location in triangulated subdivisions with O(''n'') storage space and O(log ''n'') query time.
The general idea is to build a hierarchy of triangles. To perform a query, we start by finding the top-level triangle that contains the query point. Since the number of top-level triangles is bounded by a constant, this operation can be performed in O(1) time. Each triangle has pointers to the triangles it intersects in the next level of the hierarchy, and the number of pointers is also bounded by a constant. We proceed with the query by finding which triangle contains the query point level by level.
The data structure is built in the opposite order, that is, bottom-up. We start with the triangulated subdivision, and choose an independent set of vertices to be removed. After removing the vertices, we retriangulate the subdivision. Because the subdivision is formed by triangles, a greedy algorithm can find an independent set that contains a constant fraction of the vertices. Therefore, the number of removal steps is O(log ''n'').
Trapezoidal decomposition
 A
A randomized
In common usage, randomness is the apparent or actual lack of pattern or predictability in events. A random sequence of events, symbols or steps often has no order and does not follow an intelligible pattern or combination. Individual rand ...
approach to this problem, and probably the most practical one, is based on trapezoidal decomposition
A quadrilateral with at least one pair of parallel sides is called a trapezoid () in American and Canadian English. In British and other forms of English, it is called a trapezium ().
A trapezoid is necessarily a convex quadrilateral in Eu ...
, or trapezoidal map. A trapezoidal decomposition is obtained by shooting vertical bullets going both up and down from each vertex in the original subdivision. The bullets stop when they hit an edge, and form a new edge in the subdivision. This way, we obtain a subset of the slab decomposition, with only O(''n'') edges and vertices, since for each vertex in the original subdivision we only add two new vertices and increase the number of edges by four.
It is not easy to see how to use a trapezoidal decomposition for point location, since a binary search similar to the one used in the slab decomposition can no longer be performed. Instead, we need to answer a query in the same fashion as the triangulation refinement approach, but the data structure is constructed top-down. Initially, we build a trapezoidal decomposition containing only the bounding box, and no internal vertex. Then, we add the segments from the subdivision, one by one, in random order, refining the trapezoidal decomposition. Using backwards analysis
Backward or Backwards is a relative direction.
Backwards or Sdrawkcab (the word "backwards" with its letters reversed) may also refer to:
* Backwards (Red Dwarf), "Backwards" (''Red Dwarf''), episode of sci-fi TV sitcom ''Red Dwarf''
** Backwar ...
, we can show that the expected number of trapezoids created for each insertion is bounded by a constant.
We build a directed acyclic graph
In mathematics, particularly graph theory, and computer science, a directed acyclic graph (DAG) is a directed graph with no directed cycles. That is, it consists of vertices and edges (also called ''arcs''), with each edge directed from one v ...
, where the vertices are the trapezoids that existed at some point in the refinement, and the directed edges connect the trapezoids obtained by subdivision. The expected depth of a search in this digraph, starting from the vertex corresponding to the bounding box, is O(log ''n'').
Higher dimensions
There are no known general point location data structures with linear space and logarithmic query time for dimensions greater than 2. Therefore, we need to sacrifice either query time, or storage space, or restrict ourselves to some less general type of subdivision. In three-dimensional space, it is possible to answer point location queries in O(log² ''n'') using O(''n'' log ''n'') space. The general idea is to maintain several planar point location data structures, corresponding to the intersection of the subdivision with ''n'' parallel planes that contain each subdivision vertex. A naive use of this idea would increase the storage space to O(''n''²). In the same fashion as in the slab decomposition, the similarity between consecutive data structures can be exploited in order to reduce the storage space to O(''n'' log ''n''), but the query time increases to O(log² ''n''). In ''d''-dimensional space, point location can be solved by recursively projecting the faces into a (''d''-1)-dimensional space. While the query time is O(log ''n''), the storage space can be as high as . The high complexity of the ''d''-dimensional data structures led to the study of special types of subdivision. One important example is the case ofarrangements of hyperplanes
In geometry and combinatorics, an arrangement of hyperplanes is an arrangement of a finite set ''A'' of hyperplanes in a linear, affine, or projective space ''S''.
Questions about a hyperplane arrangement ''A'' generally concern geometrical, top ...
. An arrangement of ''n'' hyperplanes defines O(''nd'') cells, but point location can be performed in O(log ''n'') time with O(''nd'') space by using Chazelle's hierarchical cutting
Cutting is the separation or opening of a physical object, into two or more portions, through the application of an acutely directed force.
Implements commonly used for cutting are the knife and saw, or in medicine and science the scalpel and ...
s.
Another special type of subdivision is called rectilinear (or orthogonal) subdivision. In a rectilinear subdivision, all edges are parallel to one of the ''d'' orthogonal axis. In this case, point location can be answered in O(log''d''-1 ''n'') time with O(''n'') space.
References
* * * * * * {{cite journal , first = David G. , last = Kirkpatrick , authorlink = David G. Kirkpatrick , title = Optimal search in planar subdivisions , journal =SIAM Journal on Computing
The ''SIAM Journal on Computing'' is a scientific journal focusing on the mathematical and formal aspects of computer science. It is published by the Society for Industrial and Applied Mathematics (SIAM).
Although its official ISO abbreviation is ...
, volume = 12
, year = 1983
, pages = 28–35
, doi = 10.1137/0212002
, issue = 1, citeseerx= 10.1.1.461.1866
External links
Point-Location Source Repository
at Stony Brook University
in
CGAL
The Computational Geometry Algorithms Library (CGAL) is an open source software library of computational geometry algorithms. While primarily written in C++, Scilab bindings and bindings generated with SWIG (supporting Python and Java for now ...
, the Computational Geometry Algorithms Library
Geometric data structures