Perturbative QCD

Perturbative quantum chromodynamics (also perturbative QCD) is a subfield of particle physics in which the theory of strong interactions, Quantum Chromodynamics (QCD), is studied by using the fact that the strong coupling constant $\alpha_s$ is small in high energy or short distance interactions, thus allowing perturbation theory techniques to be applied. In most circumstances, making testable predictions with QCD is extremely difficult, due to the infinite number of possible topologically-inequivalent interactions. Over short distances, the coupling is small enough that this infinite number of terms can be approximated accurately by a finite number of terms. Although only applicable at high energies, this approach has resulted in the most precise tests of QCD to date .

An important test of perturbative QCD is the measurement of the ratio of production rates for $e^e^ \to \text$ and $e^e^ \to \mu^\mu^$. Since only the total production rate is considered, the summation over all final-state hadrons cancels the dependence on specific hadron type, and this ratio can be calculated in perturbative QCD.

Most strong-interaction processes can not be calculated directly with perturbative QCD, since one cannot observe free quarks and gluons due to color confinement. For example, the structure hadrons has a non-perturbative nature. To account for this, physicists developed the QCD factorization theorem, which separates the cross section into two parts: the process dependent perturbatively-calculable short-distance parton cross section, and the universal long-distance functions. These universal long-distance functions can be measured with global fit to experiments and include parton distribution functions, fragmentation functions, multi-parton correlation functions, generalized parton distributions, generalized distribution amplitudes and many kinds of form factors. There are several collaborations for each kind of universal long-distance functions. They have become an important part of modern particle physics.

Mathematical formulation of QCD

Quantum chromodynamics is formulated in terms of the Lagrangian density

Expressions in the Lagrangian

Matter content

The matter content of the Lagrangian is a spinor field $\psi$ and a gauge field $A_\mu$, also known as the gluon field.

The spinor field has spin indices, on which the gamma matrices $\gamma^\mu$ act, as well as colour indices on which the covariant derivative $D_\mu$ acts. Formally the spinor field $\psi(x)$ is then a function of spacetime valued as a tensor product of a spin vector and a colour vector.

Quantum chromodynamics is a gauge theory and so has an associated gauge group $G$, which is a compact Lie group. A colour vector is an element of some representation space of $G$.

The gauge field $A_\mu$ is valued in the Lie algebra $\mathfrak$ of $G$. Similarly to the spinor field, the gauge field also has a spacetime index $\mu$, and so is valued as a co-vector tensored with an element of $\mathfrak$. In Lie theory, one can always find a basis $t^a$ of $\mathfrak$ such that $\text(t^at^b) = \delta^$. In differential geometry $A_\mu$ is known as a connection.

The gauge field does not appear explicitly in the Lagrangian but through the curvature $F_,$ defined
F_ = \partial_\mu A_\nu - \partial_\nu A_\mu + ig _\mu,A_\nu
This is known as the gluon field strength tensor or geometrically as the curvature form. The parameter $g$ is the coupling constant for QCD.

By expanding $F_$ into $F^a_$ and using Feynman slash notation, the Lagrangian can then be written schematically in a more elegant form

Gauge fixed Lagrangian

While this expression is mathematically elegant, with manifest gauge symmetry, for perturbative calculations it is necessary to fix a gauge. The gauge-fixing procedure was developed by Faddeev and Popov. It requires the introduction of ghost fields $c(x)$ which are valued in $\mathfrak.$ After the gauge fixing procedure the Lagrangian is written

{{Equation box 1
, indent =:
, equation = :$\mathcal{L} = - \frac{1}{4}(F^a_{\mu\nu})^2 - \frac{1}{2\xi}(\partial^\mu A_\mu)^2 + \bar{\psi} \left( i D\!\!\!\!/ - m\right) \psi - \bar c^a\partial^\mu(D_\mu c)^a$, border
, border colour = #50C878
, background colour = #ECFCF4

Where $\xi$ is the gauge-fixing parameter. Choosing $\xi = 1$ is known as Feynman gauge.

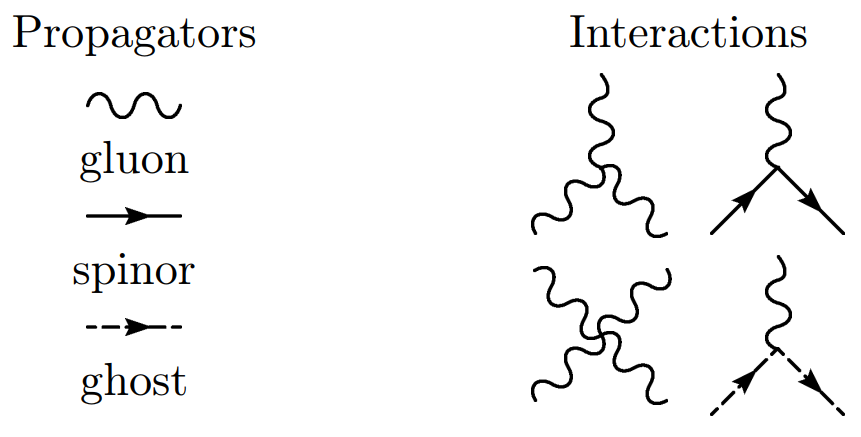
After expanding out the curvature and covariant derivatives, the Feynman rules for QCD can be derived through path integral methods.

Renormalization

The techniques for renormalization of gauge theories and QCD were developed and carried out by 't Hooft. It is known that QCD, for a small number of spinors, exhibits asymptotic freedom.

One-loop renormalization

Showing that QCD is renormalizable at one-loop order requires the evaluation of loop integrals, which can be derived from Feynman rules and evaluated using dimensional regularization.

External links

Factorization of Hard Processes in QCD

References

* Peskin, M. E., Schroeder, D. V. (1995). An Introduction to Quantum Field Theory. Westview Press.

Quantum chromodynamics