Period (algebraic geometry)

In mathematics, specifically algebraic geometry, a period or algebraic period is a complex number that can be expressed as an integral of an algebraic function over an algebraic domain. The periods are a class of numbers which includes, alongside the algebraic numbers, many well known mathematical constants such as the number π. Sums and products of periods remain periods, such that the periods $\mathcal P$ form a ring.

Maxim Kontsevich and Don Zagier gave a survey of periods and introduced some conjectures about them.

Periods play an important role in the theory of differential equations and transcendental numbers as well as in open problems of modern arithmetical algebraic geometry. They also appear when computing the integrals that arise from Feynman diagrams, and there has been intensive work trying to understand the connections.

Definition

A number $\alpha$ is a period if it can be expressed as an integral of the form

:$\alpha = \int_Q(x_1,\ldots,x_n)\ \mathrmx_1\ldots\mathrmx_n$

where $P$ is a polynomial and $Q$ a rational function on $\mathbb^n$ with rational coefficients. A complex number is a period if its real and imaginary parts are periods.

An alternative definition allows $P$ and $Q$ to be algebraic functions; this looks more general, but is equivalent. The coefficients of the rational functions and polynomials can also be generalised to algebraic numbers because irrational algebraic numbers are expressible in terms of areas of suitable domains.

In the other direction, $Q$ can be restricted to be the constant function $1$ or $-1$, by replacing the integrand with an integral of $\pm 1$ over a region defined by a polynomial in additional variables.

In other words, a (nonnegative) period is the volume of a region in $\mathbb^n$ defined by polynomial inequalities with rational coefficients.

Properties and motivation

The periods are intended to bridge the gap between the well-behaved algebraic numbers, which form a class too narrow to include many common mathematical constants and the transcendental numbers, which are uncountable and apart from very few specific examples hard to describe. The latter are also not generally computable.

The ring of periods $\mathcal P$ lies in between the fields of algebraic numbers $\mathbb \overline$ and complex numbers $\mathbb C$ and is countable. The periods themselves are all computable, and in particular definable. That is: $\mathbb \overline\sub \mathcal P\sub \mathbb C$.

Periods include some of those transcendental numbers, that can be described in an algorithmic way and only contain a finite amount of information.

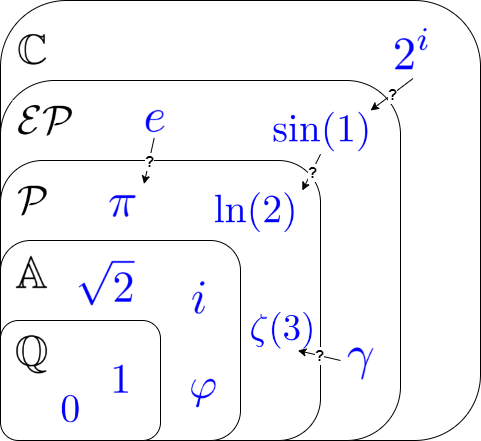
Numbers known to be periods

The following numbers are among the ones known to be periods:

Open questions

Many of the constants known to be periods are also given by integrals of transcendental functions. Kontsevich and Zagier note that there "seems to be no universal rule explaining why certain infinite sums or integrals of transcendental functions are periods".

Kontsevich and Zagier conjectured that, if a period is given by two different integrals, then each integral can be transformed into the other using only the linearity of integrals (in both the integrand and the domain), changes of variables, and the Newton–Leibniz formula

: $\int_a^b f'(x) \, dx = f(b) - f(a)$

(or, more generally, the Stokes formula).

A useful property of algebraic numbers is that equality between two algebraic expressions can be determined algorithmically. The conjecture of Kontsevich and Zagier would imply that equality of periods is also decidable: inequality of computable reals is known recursively enumerable; and conversely if two integrals agree, then an algorithm could confirm so by trying all possible ways to transform one of them into the other one.

Further open questions consist of proving which known mathematical constants do not belong to the ring of periods. An example of a real number that is not a period is given by Chaitin's constant Ω. Any other non-computable number also gives an example of a real number that is not a period. It is also possible to construct artificial examples of computable numbers which are not periods. However there are no computable numbers proven not to be periods, which have not been artificially constructed for that purpose.

It is conjectured that 1/''π,'' Euler's number ''e'' and the Euler–Mascheroni constant γ are ''not'' periods.

Kontsevich and Zagier suspect these problems to be very hard and remain open a long time.

Extensions

The ring of periods can be widened to the ring of ''extended periods'' $\hat \mathcal P$ by adjoining the element 1/''π.''

Permitting the integrand $Q$ to be the product of an algebraic function and the exponential of an algebraic function, results in another extension: the ''exponential periods'' $\mathcal \mathcal P$. They also form a ring and are countable. It is $\overline\sub \mathcal P \sube \mathcal\sub \mathbb C$.

The following numbers are among the ones known to be exponential periods:

See also

* Transcendental number theory
* Mathematical constant
* L-function
* Jacobian variety
* Gauss–Manin connection
* Mixed motives (math)
* Tannakian formalism

References

External links

PlanetMath: Period

{{Number systems

Mathematical constants
Algebraic geometry
Integral calculus
Transcendental numbers