Pearson's r on:
[Wikipedia]
[Google]
[Amazon]
 In
In
Basic Concepts of Correlation
, retrieved 22 February 2015. is where * is the
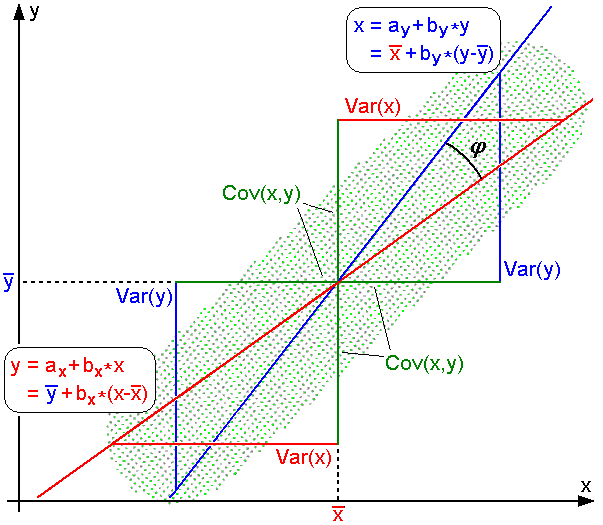 ]
For uncentered data, there is a relation between the correlation coefficient and the angle ''φ'' between the two regression lines, and , obtained by regressing ''y'' on ''x'' and ''x'' on ''y'' respectively. (Here, ''φ'' is measured counterclockwise within the first quadrant formed around the lines' intersection point if , or counterclockwise from the fourth to the second quadrant if .) One can show that if the standard deviations are equal, then , where sec and tan are
]
For uncentered data, there is a relation between the correlation coefficient and the angle ''φ'' between the two regression lines, and , obtained by regressing ''y'' on ''x'' and ''x'' on ''y'' respectively. (Here, ''φ'' is measured counterclockwise within the first quadrant formed around the lines' intersection point if , or counterclockwise from the fourth to the second quadrant if .) One can show that if the standard deviations are equal, then , where sec and tan are
 Several authors have offered guidelines for the interpretation of a correlation coefficient. However, all such criteria are in some ways arbitrary. The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
Several authors have offered guidelines for the interpretation of a correlation coefficient. However, all such criteria are in some ways arbitrary. The interpretation of a correlation coefficient depends on the context and purposes. A correlation of 0.8 may be very low if one is verifying a physical law using high-quality instruments, but may be regarded as very high in the social sciences, where there may be a greater contribution from complicating factors.
 For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson's correlation coefficient follows Student's ''t''-distribution with degrees of freedom ''n'' − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
:
has a student's ''t''-distribution in the null case (zero correlation). This holds approximately in case of non-normal observed values if sample sizes are large enough. For determining the critical values for ''r'' the inverse function is needed:
:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper provides graphs and tables for general values of ''ρ'', for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson's correlation coefficient follows a Student's ''t''-distribution, but the degrees of freedom are reduced.
For pairs from an uncorrelated bivariate normal distribution, the sampling distribution of the studentized Pearson's correlation coefficient follows Student's ''t''-distribution with degrees of freedom ''n'' − 2. Specifically, if the underlying variables have a bivariate normal distribution, the variable
:
has a student's ''t''-distribution in the null case (zero correlation). This holds approximately in case of non-normal observed values if sample sizes are large enough. For determining the critical values for ''r'' the inverse function is needed:
:
Alternatively, large sample, asymptotic approaches can be used.
Another early paper provides graphs and tables for general values of ''ρ'', for small sample sizes, and discusses computational approaches.
In the case where the underlying variables are not normal, the sampling distribution of Pearson's correlation coefficient follows a Student's ''t''-distribution, but the degrees of freedom are reduced.
statistics
Statistics (from German language, German: ', "description of a State (polity), state, a country") is the discipline that concerns the collection, organization, analysis, interpretation, and presentation of data. In applying statistics to a s ...
, the Pearson correlation coefficient (PCC) is a correlation coefficient
A correlation coefficient is a numerical measure of some type of linear correlation, meaning a statistical relationship between two variables. The variables may be two columns of a given data set of observations, often called a sample, or two c ...
that measures linear
In mathematics, the term ''linear'' is used in two distinct senses for two different properties:
* linearity of a '' function'' (or '' mapping'');
* linearity of a '' polynomial''.
An example of a linear function is the function defined by f(x) ...
correlation between two sets of data. It is the ratio between the covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables.
The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one ...
of two variables and the product of their standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
s; thus, it is essentially a normalized measurement of the covariance, such that the result always has a value between −1 and 1. As with covariance itself, the measure can only reflect a linear correlation
In statistics, correlation or dependence is any statistical relationship, whether causal or not, between two random variables or bivariate data. Although in the broadest sense, "correlation" may indicate any type of association, in statistics ...
of variables, and ignores many other types of relationships or correlations. As a simple example, one would expect the age and height of a sample of children from a school to have a Pearson correlation coefficient significantly greater than 0, but less than 1 (as 1 would represent an unrealistically perfect correlation).
Naming and history
It was developed byKarl Pearson
Karl Pearson (; born Carl Pearson; 27 March 1857 – 27 April 1936) was an English biostatistician and mathematician. He has been credited with establishing the discipline of mathematical statistics. He founded the world's first university ...
from a related idea introduced by Francis Galton
Sir Francis Galton (; 16 February 1822 – 17 January 1911) was an English polymath and the originator of eugenics during the Victorian era; his ideas later became the basis of behavioural genetics.
Galton produced over 340 papers and b ...
in the 1880s, and for which the mathematical formula was derived and published by Auguste Bravais in 1844. The naming of the coefficient is thus an example of Stigler's Law.
Motivation/Intuition and Derivation
The correlation coefficient can be derived by considering the cosine of the angle between two points representing the two sets of x and y co-ordinate data. This expression is therefore a number between -1 and 1 and is equal to unity when all the points lie on a straight line.Definition
Pearson's correlation coefficient is thecovariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables.
The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one ...
of the two variables divided by the product of their standard deviations. The form of the definition involves a "product moment", that is, the mean (the first moment about the origin) of the product of the mean-adjusted random variables; hence the modifier ''product-moment'' in the name.
For a population
Pearson's correlation coefficient, when applied to apopulation
Population is a set of humans or other organisms in a given region or area. Governments conduct a census to quantify the resident population size within a given jurisdiction. The term is also applied to non-human animals, microorganisms, and pl ...
, is commonly represented by the Greek letter ''ρ'' (rho) and may be referred to as the ''population correlation coefficient'' or the ''population Pearson correlation coefficient''. Given a pair of random variables (for example, Height and Weight), the formula for ''ρ''Real Statistics Using Excel,Basic Concepts of Correlation
, retrieved 22 February 2015. is where * is the
covariance
In probability theory and statistics, covariance is a measure of the joint variability of two random variables.
The sign of the covariance, therefore, shows the tendency in the linear relationship between the variables. If greater values of one ...
* is the standard deviation
In statistics, the standard deviation is a measure of the amount of variation of the values of a variable about its Expected value, mean. A low standard Deviation (statistics), deviation indicates that the values tend to be close to the mean ( ...
of
* is the standard deviation of .
The formula for can be expressed in terms of mean
A mean is a quantity representing the "center" of a collection of numbers and is intermediate to the extreme values of the set of numbers. There are several kinds of means (or "measures of central tendency") in mathematics, especially in statist ...
and expectation. Since
:
the formula for can also be written as
where
* and are defined as above
* is the mean of
* is the mean of
* is the expectation.
The formula for can be expressed in terms of uncentered moments. Since
:
the formula for can also be written as
For a sample
Pearson's correlation coefficient, when applied to a sample, is commonly represented by and may be referred to as the ''sample correlation coefficient'' or the ''sample Pearson correlation coefficient''. We can obtain a formula for by substituting estimates of the covariances and variances based on a sample into the formula above. Given paired data consisting of pairs, is defined as where * is sample size * are the individual sample points indexed with ''i'' * (the sample mean); and analogously for . Rearranging gives us this formula for : : where are defined as above. Rearranging again gives us this formula for : : where are defined as above. This formula suggests a convenient single-pass algorithm for calculating sample correlations, though depending on the numbers involved, it can sometimes be numerically unstable. An equivalent expression gives the formula for as the mean of the products of thestandard score
In statistics, the standard score or ''z''-score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores ...
s as follows:
:
where
* are defined as above, and are defined below
* is the standard score (and analogously for the standard score of ).
Alternative formulae for are also available. For example, one can use the following formula for :
:
where
* are defined as above and:
* (the sample standard deviation); and analogously for .
For jointly gaussian distributions
If is jointly gaussian, with mean zero andvariance
In probability theory and statistics, variance is the expected value of the squared deviation from the mean of a random variable. The standard deviation (SD) is obtained as the square root of the variance. Variance is a measure of dispersion ...
, then .
Practical issues
Under heavy noise conditions, extracting the correlation coefficient between two sets of stochastic variables is nontrivial, in particular whereCanonical Correlation Analysis
In statistics, canonical-correlation analysis (CCA), also called canonical variates analysis, is a way of inferring information from cross-covariance matrices. If we have two vectors ''X'' = (''X''1, ..., ''X'n'') and ''Y'' ...
reports degraded correlation values due to the heavy noise contributions. A generalization of the approach is given elsewhere.
In case of missing data, Garren derived the maximum likelihood
In statistics, maximum likelihood estimation (MLE) is a method of estimating the parameters of an assumed probability distribution, given some observed data. This is achieved by maximizing a likelihood function so that, under the assumed stati ...
estimator.
Some distributions (e.g., stable distribution
In probability theory, a distribution is said to be stable if a linear combination of two independent random variables with this distribution has the same distribution, up to location and scale parameters. A random variable is said to be st ...
s other than a normal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
) do not have a defined variance.
Mathematical properties
The values of both the sample and population Pearson correlation coefficients are on or between −1 and 1. Correlations equal to +1 or −1 correspond to data points lying exactly on a line (in the case of the sample correlation), or to a bivariate distribution entirely supported on a line (in the case of the population correlation). The Pearson correlation coefficient is symmetric: corr(''X'',''Y'') = corr(''Y'',''X''). A key mathematical property of the Pearson correlation coefficient is that it is invariant under separate changes in location and scale in the two variables. That is, we may transform ''X'' to and transform ''Y'' to , where ''a'', ''b'', ''c'', and ''d'' are constants with , without changing the correlation coefficient. (This holds for both the population and sample Pearson correlation coefficients.) More general linear transformations do change the correlation: see ' for an application of this. In particular, it might be useful to notice that corr(''-X'',''Y'') = -corr(''X'',''Y'')Interpretation
The correlation coefficient ranges from −1 to 1. An absolute value of exactly 1 implies that a linear equation describes the relationship between ''X'' and ''Y'' perfectly, with all data points lying on a line. The correlation sign is determined by the regression slope: a value of +1 implies that all data points lie on a line for which ''Y'' increases as ''X'' increases, whereas a value of -1 implies a line where ''Y'' increases while ''X'' decreases. A value of 0 implies that there is no linear dependency between the variables. More generally, is positive if and only if ''X''''i'' and ''Y''''i'' lie on the same side of their respective means. Thus the correlation coefficient is positive if ''X''''i'' and ''Y''''i'' tend to be simultaneously greater than, or simultaneously less than, their respective means. The correlation coefficient is negative ( anti-correlation) if ''X''''i'' and ''Y''''i'' tend to lie on opposite sides of their respective means. Moreover, the stronger either tendency is, the larger is theabsolute value
In mathematics, the absolute value or modulus of a real number x, is the non-negative value without regard to its sign. Namely, , x, =x if x is a positive number, and , x, =-x if x is negative (in which case negating x makes -x positive), ...
of the correlation coefficient.
Rodgers and Nicewander cataloged thirteen ways of interpreting correlation or simple functions of it:
* Function of raw scores and means
* Standardized covariance
* Standardized slope of the regression line
* Geometric mean of the two regression slopes
* Square root of the ratio of two variances
* Mean cross-product of standardized variables
* Function of the angle between two standardized regression lines
* Function of the angle between two variable vectors
* Rescaled variance of the difference between standardized scores
* Estimated from the balloon rule
* Related to the bivariate ellipses of isoconcentration
* Function of test statistics from designed experiments
* Ratio of two means
Geometric interpretation
 ]
For uncentered data, there is a relation between the correlation coefficient and the angle ''φ'' between the two regression lines, and , obtained by regressing ''y'' on ''x'' and ''x'' on ''y'' respectively. (Here, ''φ'' is measured counterclockwise within the first quadrant formed around the lines' intersection point if , or counterclockwise from the fourth to the second quadrant if .) One can show that if the standard deviations are equal, then , where sec and tan are
]
For uncentered data, there is a relation between the correlation coefficient and the angle ''φ'' between the two regression lines, and , obtained by regressing ''y'' on ''x'' and ''x'' on ''y'' respectively. (Here, ''φ'' is measured counterclockwise within the first quadrant formed around the lines' intersection point if , or counterclockwise from the fourth to the second quadrant if .) One can show that if the standard deviations are equal, then , where sec and tan are trigonometric functions
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all ...
.
For centered data (i.e., data which have been shifted by the sample means of their respective variables so as to have an average of zero for each variable), the correlation coefficient can also be viewed as the cosine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side opposite that ...
of the angle
In Euclidean geometry, an angle can refer to a number of concepts relating to the intersection of two straight Line (geometry), lines at a Point (geometry), point. Formally, an angle is a figure lying in a Euclidean plane, plane formed by two R ...
''θ'' between the two observed vectors in ''N''-dimensional space (for ''N'' observations of each variable).
Both the uncentered (non-Pearson-compliant) and centered correlation coefficients can be determined for a dataset. As an example, suppose five countries are found to have gross national products of 1, 2, 3, 5, and 8 billion dollars, respectively. Suppose these same five countries (in the same order) are found to have 11%, 12%, 13%, 15%, and 18% poverty. Then let x and y be ordered 5-element vectors containing the above data: and .
By the usual procedure for finding the angle ''θ'' between two vectors (see dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
), the ''uncentered'' correlation coefficient is
:
This uncentered correlation coefficient is identical with the cosine similarity. The above data were deliberately chosen to be perfectly correlated: . The Pearson correlation coefficient must therefore be exactly one. Centering the data (shifting x by and y by ) yields and , from which
:
as expected.
Interpretation of the size of a correlation
Inference
Statistical inference based on Pearson's correlation coefficient often focuses on one of the following two aims: * One aim is to test thenull hypothesis
The null hypothesis (often denoted ''H''0) is the claim in scientific research that the effect being studied does not exist. The null hypothesis can also be described as the hypothesis in which no relationship exists between two sets of data o ...
that the true correlation coefficient ''ρ'' is equal to 0, based on the value of the sample correlation coefficient ''r''.
* The other aim is to derive a confidence interval that, on repeated sampling, has a given probability of containing ''ρ''.
Methods of achieving one or both of these aims are discussed below.
Using a permutation test
Permutation tests provide a direct approach to performing hypothesis tests and constructing confidence intervals. A permutation test for Pearson's correlation coefficient involves the following two steps: # Using the original paired data (''x''''i'', ''y''''i''), randomly redefine the pairs to create a new data set (''x''''i'', ''y'''), where the ' are apermutation
In mathematics, a permutation of a set can mean one of two different things:
* an arrangement of its members in a sequence or linear order, or
* the act or process of changing the linear order of an ordered set.
An example of the first mean ...
of the set . The permutation ' is selected randomly, with equal probabilities placed on all ''n''! possible permutations. This is equivalent to drawing the ' randomly without replacement from the set . In bootstrapping
In general, bootstrapping usually refers to a self-starting process that is supposed to continue or grow without external input. Many analytical techniques are often called bootstrap methods in reference to their self-starting or self-supporting ...
, a closely related approach, the ''i'' and the ' are equal and drawn with replacement from ;
# Construct a correlation coefficient ''r'' from the randomized data.
To perform the permutation test, repeat steps (1) and (2) a large number of times. The p-value for the permutation test is the proportion of the ''r'' values generated in step (2) that are larger than the Pearson correlation coefficient that was calculated from the original data. Here "larger" can mean either that the value is larger in magnitude, or larger in signed value, depending on whether a two-sided or one-sided test is desired.
Using a bootstrap
The bootstrap can be used to construct confidence intervals for Pearson's correlation coefficient. In the "non-parametric" bootstrap, ''n'' pairs (''x''''i'', ''y''''i'') are resampled "with replacement" from the observed set of ''n'' pairs, and the correlation coefficient ''r'' is calculated based on the resampled data. This process is repeated a large number of times, and the empirical distribution of the resampled ''r'' values are used to approximate the sampling distribution of the statistic. A 95% confidence interval for ''ρ'' can be defined as the interval spanning from the 2.5th to the 97.5thpercentile
In statistics, a ''k''-th percentile, also known as percentile score or centile, is a score (e.g., a data point) a given percentage ''k'' of all scores in its frequency distribution exists ("exclusive" definition) or a score a given percentage ...
of the resampled ''r'' values.
Standard error
If and are random variables, with a simple linear relationship between them with an additive normal noise (i.e., y= a + bx + e), then a standard error associated to the correlation is : where is the correlation and the sample size.Testing using Student's ''t''-distribution
Using the exact distribution
For data that follow a bivariate normal distribution, the exact density function ''f''(''r'') for the sample correlation coefficient ''r'' of a normal bivariate is : where is thegamma function
In mathematics, the gamma function (represented by Γ, capital Greek alphabet, Greek letter gamma) is the most common extension of the factorial function to complex numbers. Derived by Daniel Bernoulli, the gamma function \Gamma(z) is defined ...
and is the Gaussian hypergeometric function.
In the special case when (zero population correlation), the exact density function ''f''(''r'') can be written as
:
where is the beta function
In mathematics, the beta function, also called the Euler integral of the first kind, is a special function that is closely related to the gamma function and to binomial coefficients. It is defined by the integral
: \Beta(z_1,z_2) = \int_0^1 t^ ...
, which is one way of writing the density of a Student's t-distribution for a studentized sample correlation coefficient, as above.
Using the Fisher transformation
In practice, confidence intervals and hypothesis tests relating to ''ρ'' are usually carried out using the, Variance-stabilizing transformation, Fisher transformation, '': : ''F''(''r'') approximately follows anormal distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is
f(x) = \frac ...
with
:and standard error
where ''n'' is the sample size. The approximation error is lowest for a large sample size and small and and increases otherwise.
Using the approximation, a z-score
In statistics, the standard score or ''z''-score is the number of standard deviations by which the value of a raw score (i.e., an observed value or data point) is above or below the mean value of what is being observed or measured. Raw scores ...
is
:
under the null hypothesis
The null hypothesis (often denoted ''H''0) is the claim in scientific research that the effect being studied does not exist. The null hypothesis can also be described as the hypothesis in which no relationship exists between two sets of data o ...
that , given the assumption that the sample pairs are independent and identically distributed and follow a bivariate normal distribution. Thus an approximate p-value can be obtained from a normal probability table. For example, if ''z'' = 2.2 is observed and a two-sided p-value is desired to test the null hypothesis that , the p-value is , where Φ is the standard normal cumulative distribution function
In probability theory and statistics, the cumulative distribution function (CDF) of a real-valued random variable X, or just distribution function of X, evaluated at x, is the probability that X will take a value less than or equal to x.
Ever ...
.
To obtain a confidence interval for ρ, we first compute a confidence interval for ''F''(''''):
: