Non-composite Polyhedron on:
[Wikipedia]
[Google]
[Amazon]
In geometry, a composite polyhedron is a convex polyhedron that produces other polyhedrons when sliced by a plane. Examples can be found in
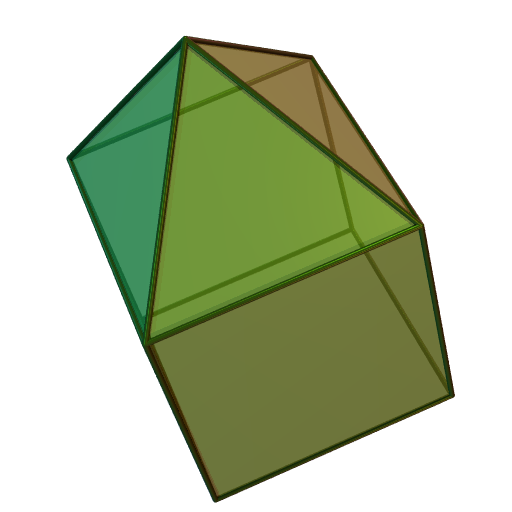Any composite polyhedron can be constructed by attaching two or more non-composite polyhedra. Alternatively, it can be defined as a convex polyhedron that can separated into two or more non-composite polyhedra. Examples can be found in a polyhedron that is constructed by attaching the regular base of
Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s.
Definition and examples
Aconvex polyhedron
In geometry, a polyhedron (: polyhedra or polyhedrons; ) is a three-dimensional figure with flat polygonal faces, straight edges and sharp corners or vertices. The term "polyhedron" may refer either to a solid figure or to its boundary su ...
is said to be ''composite'' if there exists a plane through a cycle of its edges that is not a face. Slicing the polyhedron on this plane produces two polyhedra, having together the same faces as the original polyhedron along with two new faces on the plane of the slice. Repeated slicing of this type decomposes any polyhedron into non-composite or ''elementary'' polyhedra. Some examples of non-composite polyhedron are the prism
PRISM is a code name for a program under which the United States National Security Agency (NSA) collects internet communications from various U.S. internet companies. The program is also known by the SIGAD . PRISM collects stored internet ...
s, antiprism
In geometry, an antiprism or is a polyhedron composed of two Parallel (geometry), parallel Euclidean group, direct copies (not mirror images) of an polygon, connected by an alternating band of triangles. They are represented by the Conway po ...
s, and the other seventeen Johnson solid
In geometry, a Johnson solid, sometimes also known as a Johnson–Zalgaller solid, is a convex polyhedron whose faces are regular polygons. They are sometimes defined to exclude the uniform polyhedrons. There are ninety-two Solid geometry, s ...
s. Among the regular polyhedra
A regular polyhedron is a polyhedron whose symmetry group acts transitively on its flags. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive. In classical contexts, many different eq ...
, the regular octahedron
In geometry, a regular octahedron is a Platonic solid composed of eight equilateral triangles, four of which meet at each vertex. Regular octahedra occur in nature as crystal structures. An octahedron, more generally, can be any eight-sided polyh ...
and regular icosahedron
The regular icosahedron (or simply ''icosahedron'') is a convex polyhedron that can be constructed from pentagonal antiprism by attaching two pentagonal pyramids with Regular polygon, regular faces to each of its pentagonal faces, or by putting ...
are composite.
Any composite polyhedron can be constructed by attaching two or more non-composite polyhedra. Alternatively, it can be defined as a convex polyhedron that can separated into two or more non-composite polyhedra. Examples can be found in a polyhedron that is constructed by attaching the regular base of pyramid
A pyramid () is a structure whose visible surfaces are triangular in broad outline and converge toward the top, making the appearance roughly a pyramid in the geometric sense. The base of a pyramid can be of any polygon shape, such as trian ...
s onto another polyhedron. This process is known as augmentation, although its general meaning is constructed by attaching pyramids, cupola
In architecture, a cupola () is a relatively small, usually dome-like structure on top of a building often crowning a larger roof or dome. Cupolas often serve as a roof lantern to admit light and air or as a lookout.
The word derives, via Ital ...
, and rotundas. Some Johnson solids are examples of that construction, and they have other constructions as in elongation (a polyhedron constructed by attaching those onto the bases of a prism), and gyroelongation (a polyhedron constructed by attaching those onto the bases of an antiprism).
References
{{reflist, refs= {{cite journal , last = Berman , first = Martin , year = 1971 , title = Regular-faced convex polyhedra , journal = Journal of the Franklin Institute , volume = 291 , issue = 5 , pages = 329–352 , doi = 10.1016/0016-0032(71)90071-8 , mr = 290245 {{cite book , last = Hartshorne , first = Robin , author-link = Robin Hartshorne , year = 2000 , title = Geometry: Euclid and Beyond , series = Undergraduate Texts in Mathematics , publisher = Springer-Verlag , isbn = 9780387986500 , url = https://books.google.com/books?id=EJCSL9S6la0C&pg=PA464 , page = 464 {{cite book , last = Huybers , first = P. , editor-last1 = Sloot , editor-first1 = Peter M.A. , editor-last2 = Tan , editor-first2 = C.J. Kenneth , editor-last3 = Dongaraa , editor-first3 = Jack J. , editor-last4 = Hoekstra , editor-first4 = Alfons G. , year = 2002 , contribution = The Morphology of Building Structures , contribution-url = https://books.google.com/books?id=oJpuCQAAQBAJ&pg=PA89 , title = Computational Science — ICCS 2002: International Conference Amsterdam, The Netherlands, April 21–24, 2002 Proceedings, Part III , series = Lecture Notes in Computer Science , volume = 2331 , page = 89 , doi = 10.1007/3-540-47789-6 , isbn = 978-3-540-43594-5 {{cite journal , last = Johnson , first = Norman , author-link = Norman Johnson (mathematician) , title = Convex Solids with Regular Faces , journal = Canadian Journal of Mathematics , volume = 18 , year = 1966 , pages = 169–200 , doi = 10.4153/CJM-1966-021-8 {{cite journal , last1 = Slobodan , first1 = Mišić , last2 = Obradović , first2 = Marija , last3 = Ðukanović , first3 = Gordana , title = Composite Concave Cupolae as Geometric and Architectural Forms , year = 2015 , journal = Journal for Geometry and Graphics , volume = 19 , issue = 1 , pages = 79–91 , url = https://www.heldermann-verlag.de/jgg/jgg19/j19h1misi.pdf {{cite journal , last = Timofeenko , first = A. V. , year = 2009 , title = Convex Polyhedra with Parquet Faces , journal = Docklady Mathematics , url = https://www.interocitors.com/tmp/papers/timo-parquet.pdf , volume = 80 , issue = 2 , pages = 720–723 , doi = 10.1134/S1064562409050238 {{cite journal , last = Timofeenko , first = A. V. , year = 2010 , title = Junction of Non-composite Polyhedra , journal = St. Petersburg Mathematical Journal , volume = 21 , issue = 3 , pages = 483–512 , doi = 10.1090/S1061-0022-10-01105-2 , url = https://www.ams.org/journals/spmj/2010-21-03/S1061-0022-10-01105-2/S1061-0022-10-01105-2.pdf Polyhedra Composite polyhedron