Non-Euclidean geometry on:
[Wikipedia]
[Google]
[Amazon]
 In mathematics, non-Euclidean geometry consists of two geometries based on
In mathematics, non-Euclidean geometry consists of two geometries based on
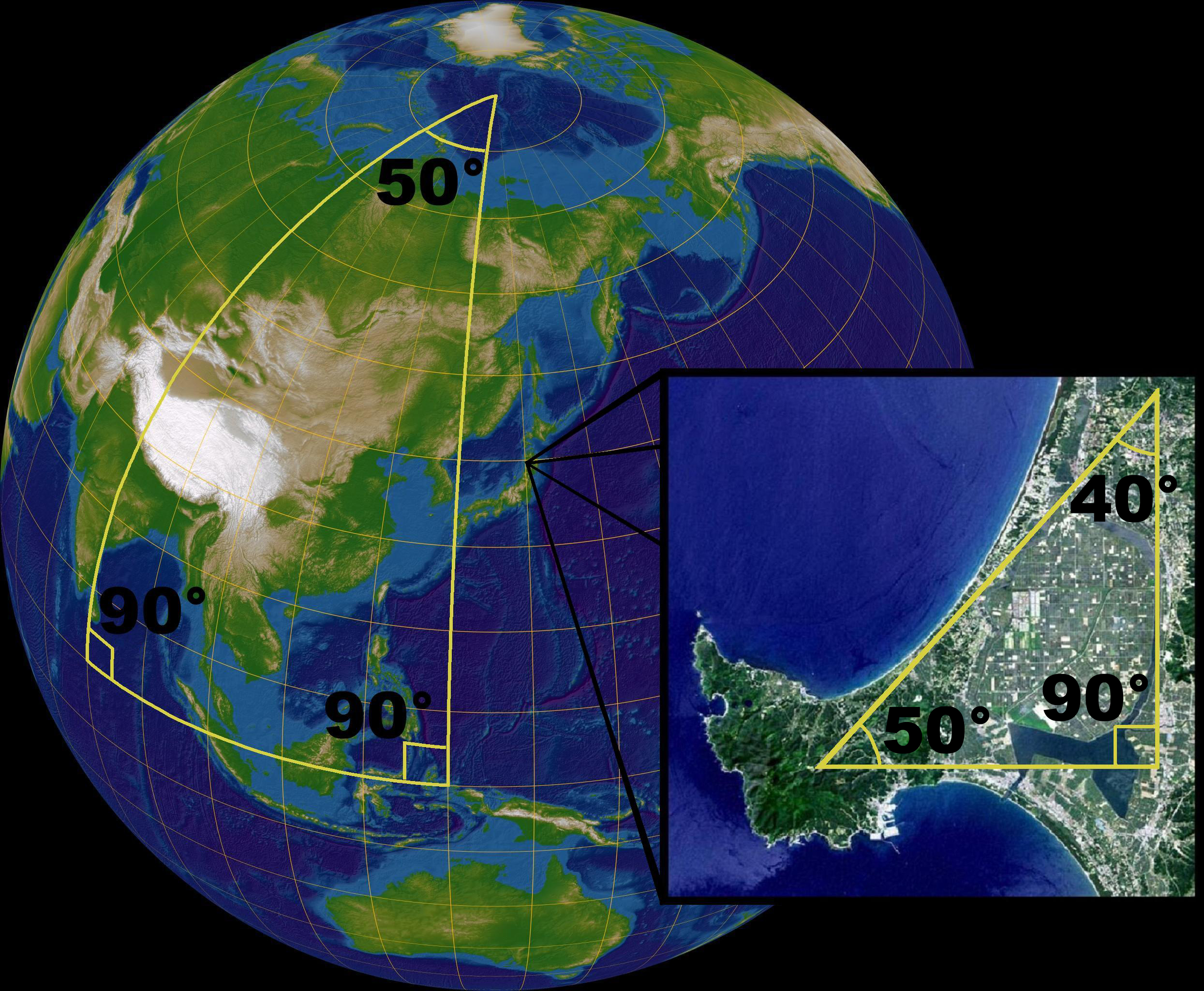 Two dimensional Euclidean geometry is modelled by our notion of a "flat plane".
Two dimensional Euclidean geometry is modelled by our notion of a "flat plane".

 Euclidean and non-Euclidean geometries naturally have many similar properties, namely those that do not depend upon the nature of parallelism. This commonality is the subject of absolute geometry (also called ''neutral geometry''). However, the properties that distinguish one geometry from others have historically received the most attention.
Besides the behavior of lines with respect to a common perpendicular, mentioned in the introduction, we also have the following:
* A Lambert quadrilateral is a quadrilateral with three right angles. The fourth angle of a Lambert quadrilateral is acute if the geometry is hyperbolic, a right angle if the geometry is Euclidean or obtuse if the geometry is elliptic. Consequently, rectangles exist (a statement equivalent to the parallel postulate) only in Euclidean geometry.
* A
Euclidean and non-Euclidean geometries naturally have many similar properties, namely those that do not depend upon the nature of parallelism. This commonality is the subject of absolute geometry (also called ''neutral geometry''). However, the properties that distinguish one geometry from others have historically received the most attention.
Besides the behavior of lines with respect to a common perpendicular, mentioned in the introduction, we also have the following:
* A Lambert quadrilateral is a quadrilateral with three right angles. The fourth angle of a Lambert quadrilateral is acute if the geometry is hyperbolic, a right angle if the geometry is Euclidean or obtuse if the geometry is elliptic. Consequently, rectangles exist (a statement equivalent to the parallel postulate) only in Euclidean geometry.
* A
Hyperbolic geometry: The first 150 years
', Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9ŌĆō24. * * * Stewart, Ian (2001) '' Flatterland'', New York: Perseus Publishing (softcover) * John Stillwell (1996) ''Sources of Hyperbolic Geometry'',
Non-Euclidean Geometry
Open Court, Chicago.
*
Non-Euclidean geometries
from ''Encyclopedia of Math'' of
Synthetic Spacetime
a digest of the axioms used, and theorems proved, by Wilson and Lewis. Archived by WebCite. {{DEFAULTSORT:Non-Euclidean Geometry
axiom
An axiom, postulate, or assumption is a statement that is taken to be true, to serve as a premise or starting point for further reasoning and arguments. The word comes from the Ancient Greek word (), meaning 'that which is thought worthy o ...
s closely related to those that specify Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
. As Euclidean geometry lies at the intersection of metric geometry and affine geometry, non-Euclidean geometry arises by either replacing the parallel postulate with an alternative, or relaxing the metric requirement. In the former case, one obtains hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆōLobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P' ...
and elliptic geometry, the traditional non-Euclidean geometries. When the metric requirement is relaxed, then there are affine planes associated with the planar algebras, which give rise to kinematic geometries that have also been called non-Euclidean geometry.
The essential difference between the metric geometries is the nature of parallel lines. Euclid
Euclid (; grc-gre, ╬ĢßĮÉ╬║╬╗╬Ą╬»╬┤╬ĘŽé; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Elements'' treatise, which established the foundations of ...
's fifth postulate, the parallel postulate, is equivalent to Playfair's postulate, which states that, within a two-dimensional plane, for any given line and a point ''A'', which is not on , there is exactly one line through ''A'' that does not intersect . In hyperbolic geometry, by contrast, there are infinitely many lines through ''A'' not intersecting , while in elliptic geometry, any line through ''A'' intersects .
Another way to describe the differences between these geometries is to consider two straight lines indefinitely extended in a two-dimensional plane that are both perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or ŽĆ/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', Ō¤é. It can ...
to a third line (in the same plane):
*In Euclidean geometry, the lines remain at a constant distance from each other (meaning that a line drawn perpendicular to one line at any point will intersect the other line and the length of the line segment joining the points of intersection remains constant) and are known as parallels.
*In hyperbolic geometry, they "curve away" from each other, increasing in distance as one moves further from the points of intersection with the common perpendicular; these lines are often called ultraparallels.
*In elliptic geometry, the lines "curve toward" each other and intersect.
History
Background
Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematician Euclid, which he described in his textbook on geometry: the ''Elements''. Euclid's approach consists in assuming a small set of intuitively appealing axioms ...
, named after the Greek mathematician
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathem ...
Euclid
Euclid (; grc-gre, ╬ĢßĮÉ╬║╬╗╬Ą╬»╬┤╬ĘŽé; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Elements'' treatise, which established the foundations of ...
, includes some of the oldest known mathematics, and geometries that deviated from this were not widely accepted as legitimate until the 19th century.
The debate that eventually led to the discovery of the non-Euclidean geometries began almost as soon as Euclid wrote ''Elements
Element or elements may refer to:
Science
* Chemical element, a pure substance of one type of atom
* Heating element, a device that generates heat by electrical resistance
* Orbital elements, parameters required to identify a specific orbit of ...
''. In the ''Elements'', Euclid begins with a limited number of assumptions (23 definitions, five common notions, and five postulates) and seeks to prove all the other results (proposition
In logic and linguistics, a proposition is the meaning of a declarative sentence. In philosophy, "meaning" is understood to be a non-linguistic entity which is shared by all sentences with the same meaning. Equivalently, a proposition is the no ...
s) in the work. The most notorious of the postulates is often referred to as "Euclid's Fifth Postulate", or simply the '' parallel postulate'', which in Euclid's original formulation is:
If a straight line falls on two straight lines in such a manner that the interior angles on the same side are together less than two right angles, then the straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.Other mathematicians have devised simpler forms of this property. Regardless of the form of the postulate, however, it consistently appears more complicated than Euclid's other postulates:
1. To draw a straight line from any point to any point. 2. To produce xtenda finite straight line continuously in a straight line. 3. To describe a circle with any centre and distance adius 4. That all right angles are equal to one another.For at least a thousand years, geometers were troubled by the disparate complexity of the fifth postulate, and believed it could be proved as a theorem from the other four. Many attempted to find a proof by contradiction, including
Ibn al-Haytham
ßĖżasan Ibn al-Haytham, Latinized as Alhazen (; full name ; ), was a medieval mathematician, astronomer, and physicist of the Islamic Golden Age from present-day Iraq.For the description of his main fields, see e.g. ("He is one of the prin ...
(Alhazen, 11th century), Omar Khayy├Īm (12th century), Nas─½r al-D─½n al-T┼½s─½ (13th century), and Giovanni Girolamo Saccheri (18th century).
The theorems of Ibn al-Haytham, Khayyam and al-Tusi on quadrilaterals, including the Lambert quadrilateral and Saccheri quadrilateral
A Saccheri quadrilateral (also known as a KhayyamŌĆōSaccheri quadrilateral) is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book ''Euclides ab omni na ...
, were "the first few theorems of the hyperbolic and the elliptic geometries". These theorems along with their alternative postulates, such as Playfair's axiom, played an important role in the later development of non-Euclidean geometry. These early attempts at challenging the fifth postulate had a considerable influence on its development among later European geometers, including Witelo, Levi ben Gerson, Alfonso, John Wallis and Saccheri. All of these early attempts made at trying to formulate non-Euclidean geometry, however, provided flawed proofs of the parallel postulate, containing assumptions that were essentially equivalent to the parallel postulate. These early attempts did, however, provide some early properties of the hyperbolic and elliptic geometries.
Khayyam, for example, tried to derive it from an equivalent postulate he formulated from "the principles of the Philosopher" (Aristotle
Aristotle (; grc-gre, ß╝łŽü╬╣ŽāŽä╬┐Žä╬Ł╬╗╬ĘŽé ''Aristot├®l─ōs'', ; 384ŌĆō322 BC) was a Greek philosopher and polymath during the Classical Greece, Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatet ...
): "Two convergent straight lines intersect and it is impossible for two convergent straight lines to diverge in the direction in which they converge." Khayyam then considered the three cases right, obtuse, and acute that the summit angles of a Saccheri quadrilateral can take and after proving a number of theorems about them, he correctly refuted the obtuse and acute cases based on his postulate and hence derived the classic postulate of Euclid, which he didn't realize was equivalent to his own postulate. Another example is al-Tusi's son, Sadr al-Din (sometimes known as "Pseudo-Tusi"), who wrote a book on the subject in 1298, based on al-Tusi's later thoughts, which presented another hypothesis equivalent to the parallel postulate. "He essentially revised both the Euclidean system of axioms and postulates and the proofs of many propositions from the ''Elements''." His work was published in Rome
, established_title = Founded
, established_date = 753 BC
, founder = King Romulus ( legendary)
, image_map = Map of comune of Rome (metropolitan city of Capital Rome, region Lazio, Italy).svg
, map_caption ...
in 1594 and was studied by European geometers, including SaccheriVictor J. Katz (1998), ''History of Mathematics: An Introduction'', p. 270ŌĆō271, AddisonŌĆōWesley, : "But in a manuscript probably written by his son Sadr al-Din in 1298, based on Nasir al-Din's later thoughts on the subject, there is a new argument based on another hypothesis, also equivalent to Euclid's, ..The importance of this latter work is that it was published in Rome in 1594 and was studied by European geometers. In particular, it became the starting point for the work of Saccheri and ultimately for the discovery of non-Euclidean geometry."who criticised this work as well as that of Wallis. Giordano Vitale, in his book ''Euclide restituo'' (1680, 1686), used the Saccheri quadrilateral to prove that if three points are equidistant on the base AB and the summit CD, then AB and CD are everywhere equidistant. In a work titled ''Euclides ab Omni Naevo Vindicatus'' (''Euclid Freed from All Flaws''), published in 1733, Saccheri quickly discarded elliptic geometry as a possibility (some others of Euclid's axioms must be modified for elliptic geometry to work) and set to work proving a great number of results in hyperbolic geometry. He finally reached a point where he believed that his results demonstrated the impossibility of hyperbolic geometry. His claim seems to have been based on Euclidean presuppositions, because no ''logical'' contradiction was present. In this attempt to prove Euclidean geometry he instead unintentionally discovered a new viable geometry, but did not realize it. In 1766 Johann Lambert wrote, but did not publish, ''Theorie der Parallellinien'' in which he attempted, as Saccheri did, to prove the fifth postulate. He worked with a figure now known as a ''Lambert quadrilateral'', a quadrilateral with three right angles (can be considered half of a Saccheri quadrilateral). He quickly eliminated the possibility that the fourth angle is obtuse, as had Saccheri and Khayyam, and then proceeded to prove many theorems under the assumption of an acute angle. Unlike Saccheri, he never felt that he had reached a contradiction with this assumption. He had proved the non-Euclidean result that the sum of the angles in a triangle increases as the area of the triangle decreases, and this led him to speculate on the possibility of a model of the acute case on a sphere of imaginary radius. He did not carry this idea any further. At this time it was widely believed that the universe worked according to the principles of Euclidean geometry.
Discovery of non-Euclidean geometry
The beginning of the 19th century would finally witness decisive steps in the creation of non-Euclidean geometry. Circa 1813,Carl Friedrich Gauss
Johann Carl Friedrich Gauss (; german: Gau├¤ ; la, Carolus Fridericus Gauss; 30 April 177723 February 1855) was a German mathematician and physicist who made significant contributions to many fields in mathematics and science. Sometimes refe ...
and independently around 1818, the German professor of law Ferdinand Karl Schweikart had the germinal ideas of non-Euclidean geometry worked out, but neither published any results. Schweikart's nephew Franz Taurinus did publish important results of hyperbolic trigonometry in two papers in 1825 and 1826, yet while admitting the internal consistency of hyperbolic geometry, he still believed in the special role of Euclidean geometry.
Then, in 1829ŌĆō1830 the Russia
Russia (, , ), or the Russian Federation, is a transcontinental country spanning Eastern Europe and Northern Asia. It is the largest country in the world, with its internationally recognised territory covering , and encompassing one-eigh ...
n mathematician Nikolai Ivanovich Lobachevsky and in 1832 the Hungarian mathematician J├Īnos Bolyai
J├Īnos Bolyai (; 15 December 1802 ŌĆō 27 January 1860) or Johann Bolyai, was a Hungarian mathematician, who developed absolute geometryŌĆöa geometry that includes both Euclidean geometry and hyperbolic geometry. The discovery of a consist ...
separately and independently published treatises on hyperbolic geometry. Consequently, hyperbolic geometry is called Lobachevskian or Bolyai-Lobachevskian geometry, as both mathematicians, independent of each other, are the basic authors of non-Euclidean geometry. Gauss mentioned to Bolyai's father, when shown the younger Bolyai's work, that he had developed such a geometry several years before, though he did not publish. While Lobachevsky created a non-Euclidean geometry by negating the parallel postulate, Bolyai worked out a geometry where both the Euclidean and the hyperbolic geometry are possible depending on a parameter ''k''. Bolyai ends his work by mentioning that it is not possible to decide through mathematical reasoning alone if the geometry of the physical universe is Euclidean or non-Euclidean; this is a task for the physical sciences.
Bernhard Riemann, in a famous lecture in 1854, founded the field of Riemannian geometry, discussing in particular the ideas now called manifolds, Riemannian metric, and curvature.
He constructed an infinite family of non-Euclidean geometries by giving a formula for a family of Riemannian metrics on the unit ball in Euclidean space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean sp ...
. The simplest of these is called elliptic geometry and it is considered a non-Euclidean geometry due to its lack of parallel lines.
By formulating the geometry in terms of a curvature tensor
In mathematics, a tensor is an algebraic object that describes a multilinear relationship between sets of algebraic objects related to a vector space. Tensors may map between different objects such as vectors, scalars, and even other tens ...
, Riemann allowed non-Euclidean geometry to apply to higher dimensions. Beltrami (1868) was the first to apply Riemann's geometry to spaces of negative curvature.
Terminology
It was Gauss who coined the term "non-Euclidean geometry". He was referring to his own work, which today we call ''hyperbolic geometry''. Several modern authors still consider ''non-Euclidean geometry'' and ''hyperbolic geometry'' synonyms. Arthur Cayley noted that distance between points inside a conic could be defined in terms oflogarithm
In mathematics, the logarithm is the inverse function to exponentiation. That means the logarithm of a number to the base is the exponent to which must be raised, to produce . For example, since , the ''logarithm base'' 10 of ...
and the projective cross-ratio function. The method has become called the CayleyŌĆōKlein metric because Felix Klein exploited it to describe the non-Euclidean geometries in articles in 1871 and 1873 and later in book form. The CayleyŌĆōKlein metrics provided working models of hyperbolic and elliptic metric geometries, as well as Euclidean geometry.
Klein is responsible for the terms "hyperbolic" and "elliptic" (in his system he called Euclidean geometry ''parabolic'', a term that generally fell out of use). His influence has led to the current usage of the term "non-Euclidean geometry" to mean either "hyperbolic" or "elliptic" geometry.
There are some mathematicians who would extend the list of geometries that should be called "non-Euclidean" in various ways.
Axiomatic basis of non-Euclidean geometry
Euclidean geometry can be axiomatically described in several ways. Unfortunately, Euclid's original system of five postulates (axioms) is not one of these, as his proofs relied on several unstated assumptions that should also have been taken as axioms. Hilbert's system consisting of 20 axioms most closely follows the approach of Euclid and provides the justification for all of Euclid's proofs. Other systems, using different sets of undefined terms obtain the same geometry by different paths. All approaches, however, have an axiom that is logically equivalent to Euclid's fifth postulate, the parallel postulate. Hilbert uses the Playfair axiom form, while Birkhoff, for instance, uses the axiom that says that, "There exists a pair of similar but not congruent triangles." In any of these systems, removal of the one axiom equivalent to the parallel postulate, in whatever form it takes, and leaving all the other axioms intact, produces absolute geometry. As the first 28 propositions of Euclid (in ''The Elements'') do not require the use of the parallel postulate or anything equivalent to it, they are all true statements in absolute geometry. To obtain a non-Euclidean geometry, the parallel postulate (or its equivalent) ''must'' be replaced by itsnegation
In logic, negation, also called the logical complement, is an operation that takes a proposition P to another proposition "not P", written \neg P, \mathord P or \overline. It is interpreted intuitively as being true when P is false, and fals ...
. Negating the Playfair's axiom form, since it is a compound statement (... there exists one and only one ...), can be done in two ways:
* Either there will exist more than one line through the point parallel to the given line or there will exist no lines through the point parallel to the given line. In the first case, replacing the parallel postulate (or its equivalent) with the statement "In a plane, given a point P and a line not passing through P, there exist two lines through P, which do not meet " and keeping all the other axioms, yields hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆōLobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P' ...
.
* The second case is not dealt with as easily. Simply replacing the parallel postulate with the statement, "In a plane, given a point P and a line not passing through P, all the lines through P meet ", does not give a consistent set of axioms. This follows since parallel lines exist in absolute geometry, but this statement says that there are no parallel lines. This problem was known (in a different guise) to Khayyam, Saccheri and Lambert and was the basis for their rejecting what was known as the "obtuse angle case". To obtain a consistent set of axioms that includes this axiom about having no parallel lines, some other axioms must be tweaked. These adjustments depend upon the axiom system used. Among others, these tweaks have the effect of modifying Euclid's second postulate from the statement that line segments can be extended indefinitely to the statement that lines are unbounded. Riemann's elliptic geometry emerges as the most natural geometry satisfying this axiom.
Models of non-Euclidean geometry
 Two dimensional Euclidean geometry is modelled by our notion of a "flat plane".
Two dimensional Euclidean geometry is modelled by our notion of a "flat plane".
Elliptic geometry
The simplest model for elliptic geometry is a sphere, where lines are " great circles" (such as theequator
The equator is a circle of latitude, about in circumference, that divides Earth into the Northern and Southern hemispheres. It is an imaginary line located at 0 degrees latitude, halfway between the North and South poles. The term can al ...
or the meridian
Meridian or a meridian line (from Latin ''meridies'' via Old French ''meridiane'', meaning ŌĆ£middayŌĆØ) may refer to
Science
* Meridian (astronomy), imaginary circle in a plane perpendicular to the planes of the celestial equator and horizon
* ...
s on a globe
A globe is a spherical model of Earth, of some other celestial body, or of the celestial sphere. Globes serve purposes similar to maps, but unlike maps, they do not distort the surface that they portray except to scale it down. A model glo ...
), and points opposite each other (called antipodal points) are identified (considered the same). This is also one of the standard models of the real projective plane. The difference is that as a model of elliptic geometry a metric is introduced permitting the measurement of lengths and angles, while as a model of the projective plane there is no such metric.
In the elliptic model, for any given line and a point ''A'', which is not on , all lines through ''A'' will intersect .
Hyperbolic geometry
Even after the work of Lobachevsky, Gauss, and Bolyai, the question remained: "Does such a model exist forhyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆōLobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P' ...
?". The model for hyperbolic geometry
In mathematics, hyperbolic geometry (also called Lobachevskian geometry or BolyaiŌĆōLobachevskian geometry) is a non-Euclidean geometry. The parallel postulate of Euclidean geometry is replaced with:
:For any given line ''R'' and point ''P' ...
was answered by Eugenio Beltrami, in 1868, who first showed that a surface called the pseudosphere has the appropriate curvature to model a portion of hyperbolic space and in a second paper in the same year, defined the Klein model, which models the entirety of hyperbolic space, and used this to show that Euclidean geometry and hyperbolic geometry were equiconsistent
In mathematical logic, two theories are equiconsistent if the consistency of one theory implies the consistency of the other theory, and vice versa. In this case, they are, roughly speaking, "as consistent as each other".
In general, it is not ...
so that hyperbolic geometry was logically consistent
In classical deductive logic, a consistent theory is one that does not lead to a logical contradiction. The lack of contradiction can be defined in either semantic or syntactic terms. The semantic definition states that a theory is consisten ...
if and only if Euclidean geometry was. (The reverse implication follows from the horosphere model of Euclidean geometry.)
In the hyperbolic model, within a two-dimensional plane, for any given line and a point ''A'', which is not on , there are infinitely many lines through ''A'' that do not intersect .
In these models, the concepts of non-Euclidean geometries are represented by Euclidean objects in a Euclidean setting. This introduces a perceptual distortion wherein the straight lines of the non-Euclidean geometry are represented by Euclidean curves that visually bend. This "bending" is not a property of the non-Euclidean lines, only an artifice of the way they are represented.
Three-dimensional non-Euclidean geometry
In three dimensions, there are eight models of geometries. There are Euclidean, elliptic, and hyperbolic geometries, as in the two-dimensional case; mixed geometries that are partially Euclidean and partially hyperbolic or spherical; twisted versions of the mixed geometries; and one unusual geometry that is completely anisotropic (i.e. every direction behaves differently).Uncommon properties
Saccheri quadrilateral
A Saccheri quadrilateral (also known as a KhayyamŌĆōSaccheri quadrilateral) is a quadrilateral with two equal sides perpendicular to the base. It is named after Giovanni Gerolamo Saccheri, who used it extensively in his book ''Euclides ab omni na ...
is a quadrilateral with two sides of equal length, both perpendicular to a side called the ''base''. The other two angles of a Saccheri quadrilateral are called the ''summit angles'' and they have equal measure. The summit angles of a Saccheri quadrilateral are acute if the geometry is hyperbolic, right angles if the geometry is Euclidean and obtuse angles if the geometry is elliptic.
* The sum of the measures of the angles of any triangle is less than 180┬░ if the geometry is hyperbolic, equal to 180┬░ if the geometry is Euclidean, and greater than 180┬░ if the geometry is elliptic. The ''defect'' of a triangle is the numerical value (180┬░ − sum of the measures of the angles of the triangle). This result may also be stated as: the defect of triangles in hyperbolic geometry is positive, the defect of triangles in Euclidean geometry is zero, and the defect of triangles in elliptic geometry is negative.
Importance
Before the models of a non-Euclidean plane were presented by Beltrami, Klein, and Poincar├®, Euclidean geometry stood unchallenged as themathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used in the natural sciences (such as physics, ...
of space
Space is the boundless three-dimensional extent in which objects and events have relative position and direction. In classical physics, physical space is often conceived in three linear dimensions, although modern physicists usually con ...
. Furthermore, since the substance of the subject in synthetic geometry was a chief exhibit of rationality, the Euclidean point of view represented absolute authority.
The discovery of the non-Euclidean geometries had a ripple effect which went far beyond the boundaries of mathematics and science. The philosopher Immanuel Kant
Immanuel Kant (, , ; 22 April 1724 ŌĆō 12 February 1804) was a German philosopher and one of the central Enlightenment thinkers. Born in K├Čnigsberg, Kant's comprehensive and systematic works in epistemology, metaphysics, ethics, and aes ...
's treatment of human knowledge had a special role for geometry. It was his prime example of synthetic a priori knowledge; not derived from the senses nor deduced through logic ŌĆö our knowledge of space was a truth that we were born with. Unfortunately for Kant, his concept of this unalterably true geometry was Euclidean. Theology was also affected by the change from absolute truth to relative truth in the way that mathematics is related to the world around it, that was a result of this paradigm shift.
Non-Euclidean geometry is an example of a scientific revolution
The Scientific Revolution was a series of events that marked the emergence of modern science during the early modern period, when developments in mathematics, physics, astronomy, biology (including human anatomy) and chemistry transformed ...
in the history of science
The history of science covers the development of science from ancient times to the present. It encompasses all three major branches of science: natural, social, and formal.
Science's earliest roots can be traced to Ancient Egypt and Meso ...
, in which mathematicians and scientists changed the way they viewed their subjects. Some geometers called Lobachevsky the "Copernicus
Nicolaus Copernicus (; pl, Miko┼éaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 ŌĆō 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formula ...
of Geometry" due to the revolutionary character of his work.
The existence of non-Euclidean geometries impacted the intellectual life of Victorian England in many ways and in particular was one of the leading factors that caused a re-examination of the teaching of geometry based on Euclid's Elements
The ''Elements'' ( grc, ╬ŻŽä╬┐╬╣Žć╬Ąß┐¢╬▒ ''Stoikhe├«a'') is a mathematical treatise consisting of 13 books attributed to the ancient Greek mathematician Euclid in Alexandria, Ptolemaic Egypt 300 BC. It is a collection of definitions, postu ...
. This curriculum issue was hotly debated at the time and was even the subject of a book, '' Euclid and his Modern Rivals'', written by Charles Lutwidge Dodgson (1832ŌĆō1898) better known as Lewis Carroll, the author of '' Alice in Wonderland''.
Planar algebras
In analytic geometry a plane is described with Cartesian coordinates : ''C'' = . The points are sometimes identified with complex numbers where ╬Ą2 Ōłł . The Euclidean plane corresponds to the case since the modulus of is given by : and this quantity is the square of the Euclidean distance between and the origin. For instance, is theunit circle
In mathematics, a unit circle is a circle of unit radiusŌĆöthat is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucli ...
.
For planar algebra, non-Euclidean geometry arises in the other cases.
When , then is a split-complex number and conventionally replaces epsilon. Then
:
and is the unit hyperbola.
When , then is a dual number.
This approach to non-Euclidean geometry explains the non-Euclidean angles: the parameters of slope
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is used ...
in the dual number plane and hyperbolic angle in the split-complex plane correspond to angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the '' vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ...
in Euclidean geometry. Indeed, they each arise in polar decomposition of a complex number .
Kinematic geometries
Hyperbolic geometry found an application in kinematics with thephysical cosmology
Physical cosmology is a branch of cosmology concerned with the study of cosmological models. A cosmological model, or simply cosmology, provides a description of the largest-scale structures and dynamics of the universe and allows study of f ...
introduced by Hermann Minkowski
Hermann Minkowski (; ; 22 June 1864 ŌĆō 12 January 1909) was a German mathematician and professor at K├Čnigsberg, Z├╝rich and G├Čttingen. He created and developed the geometry of numbers and used geometrical methods to solve problems in numb ...
in 1908. Minkowski introduced terms like worldline and proper time into mathematical physics
Mathematical physics refers to the development of mathematics, mathematical methods for application to problems in physics. The ''Journal of Mathematical Physics'' defines the field as "the application of mathematics to problems in physics and t ...
. He realized that the submanifold, of events one moment of proper time into the future, could be considered a hyperbolic space of three dimensions.
Already in the 1890s Alexander Macfarlane was charting this submanifold through his Algebra of Physics and hyperbolic quaternion
In abstract algebra, the algebra of hyperbolic quaternions is a nonassociative algebra over the real numbers with elements of the form
:q = a + bi + cj + dk, \quad a,b,c,d \in \mathbb \!
where the squares of i, j, and k are +1 and distinct elemen ...
s, though Macfarlane did not use cosmological language as Minkowski did in 1908. The relevant structure is now called the hyperboloid model of hyperbolic geometry.
The non-Euclidean planar algebras support kinematic geometries in the plane. For instance, the split-complex number ''z'' = e''a''j can represent a spacetime event one moment into the future of a frame of reference of rapidity ''a''. Furthermore, multiplication by ''z'' amounts to a Lorentz boost mapping the frame with rapidity zero to that with rapidity ''a''.
Kinematic study makes use of the dual numbers to represent the classical description of motion in absolute time and space
Absolute space and time is a concept in physics and philosophy about the properties of the universe. In physics, absolute space and time may be a preferred frame.
Before Newton
A version of the concept of absolute space (in the sense of a preferr ...
:
The equations are equivalent to a shear mapping in linear algebra:
:
With dual numbers the mapping is
Another view of special relativity
In physics, the special theory of relativity, or special relativity for short, is a scientific theory regarding the relationship between space and time. In Albert Einstein's original treatment, the theory is based on two postulates:
# The law ...
as a non-Euclidean geometry was advanced by E. B. Wilson and Gilbert Lewis in ''Proceedings of the American Academy of Arts and Sciences
The American Academy of Arts and Sciences (abbreviation: AAA&S) is one of the oldest learned societies in the United States. It was founded in 1780 during the American Revolution by John Adams, John Hancock, James Bowdoin, Andrew Oliver, ...
'' in 1912. They revamped the analytic geometry implicit in the split-complex number algebra into synthetic geometry of premises and deductions.
Fiction
Non-Euclidean geometry often makes appearances in works ofscience fiction
Science fiction (sometimes shortened to Sci-Fi or SF) is a genre of speculative fiction which typically deals with imagination, imaginative and futuristic concepts such as advanced science and technology, space exploration, time travel, Paral ...
and fantasy
Fantasy is a genre of speculative fiction involving magical elements, typically set in a fictional universe and sometimes inspired by mythology and folklore. Its roots are in oral traditions, which then became fantasy literature and drama ...
.
* In 1895, H. G. Wells published the short story "The Remarkable Case of Davidson's Eyes". To appreciate this story one should know how antipodal points on a sphere are identified in a model of the elliptic plane. In the story, in the midst of a thunderstorm, Sidney Davidson sees "Waves and a remarkably neat schooner" while working in an electrical laboratory at Harlow Technical College. At the story's close, Davidson proves to have witnessed H.M.S. ''Fulmar'' off Antipodes Island
In geography, the antipode () of any spot on Earth is the point on Earth's surface diametrically opposite to it. A pair of points ''antipodal'' () to each other are situated such that a straight line connecting the two would pass through ...
.
* Non-Euclidean geometry is sometimes connected with the influence of the 20th-century horror fiction
Horror is a genre of fiction which is intended to frighten, scare, or disgust. Horror is often divided into the sub-genres of psychological horror and supernatural horror, which is in the realm of speculative fiction. Literary historian J. ...
writer H. P. Lovecraft. In his works, many unnatural things follow their own unique laws of geometry: in Lovecraft's Cthulhu Mythos, the sunken city of R'lyeh is characterized by its non-Euclidean geometry. It is heavily implied this is achieved as a side effect of not following the natural laws of this universe rather than simply using an alternate geometric model, as the sheer innate wrongness of it is said to be capable of driving those who look upon it insane.
* The main character in Robert Pirsig's '' Zen and the Art of Motorcycle Maintenance'' mentioned Riemannian Geometry on multiple occasions.
* In '' The Brothers Karamazov'', Dostoevsky discusses non-Euclidean geometry through his character Ivan.
* Christopher Priest's novel '' Inverted World'' describes the struggle of living on a planet with the form of a rotating pseudosphere.
* Robert Heinlein's '' The Number of the Beast'' utilizes non-Euclidean geometry to explain instantaneous transport through space and time and between parallel and fictional universes.
* Zeno Rogue's '' HyperRogue'' is a roguelike game set on the hyperbolic plane, allowing the player to experience many properties of this geometry. Many mechanics, quests, and locations are strongly dependent on the features of hyperbolic geometry.
* In the Renegade Legion science fiction
Science fiction (sometimes shortened to Sci-Fi or SF) is a genre of speculative fiction which typically deals with imagination, imaginative and futuristic concepts such as advanced science and technology, space exploration, time travel, Paral ...
setting for FASA's wargame, role-playing-game and fiction, faster-than-light travel and communications is possible through the use of Hsieh Ho's Polydimensional Non-Euclidean Geometry, published sometime in the middle of the 22nd century.
* In Ian Stewart's '' Flatterland'' the protagonist
A protagonist () is the main character of a story. The protagonist makes key decisions that affect the plot, primarily influencing the story and propelling it forward, and is often the character who faces the most significant obstacles. If a st ...
Victoria Line visits all kinds of non-Euclidean worlds.
See also
* Hyperbolic space * L├®n├Īrt sphere *Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting, pr ...
* Non-Euclidean surface growth
Notes
References
*, (2012) ''Notes on hyperbolic geometry'', in: Strasbourg Master class on Geometry, pp. 1ŌĆō182, IRMA Lectures in Mathematics and Theoretical Physics, Vol. 18, Z├╝rich: European Mathematical Society (EMS), 461 pages, , DOI:10.4171/105. * Anderson, James W. ''Hyperbolic Geometry'', second edition, Springer, 2005 * Beltrami, Eugenio ''Teoria fondamentale degli spaz├« di curvatura costante'', Annali. di Mat., ser II 2 (1868), 232ŌĆō255 * *Carroll, Lewis
Charles Lutwidge Dodgson (; 27 January 1832 ŌĆō 14 January 1898), better known by his pen name Lewis Carroll, was an English author, poet and mathematician. His most notable works are '' Alice's Adventures in Wonderland'' (1865) and its seque ...
''Euclid and His Modern Rivals'', New York: Barnes and Noble, 2009 (reprint)
* H. S. M. Coxeter (1942) ''Non-Euclidean Geometry'', University of Toronto Press
The University of Toronto Press is a Canadian university press founded in 1901. Although it was founded in 1901, the press did not actually publish any books until 1911.
The press originally printed only examination books and the university cale ...
, reissued 1998 by Mathematical Association of America, .
*
* Jeremy Gray (1989) ''Ideas of Space: Euclidean, Non-Euclidean, and Relativistic'', 2nd edition, Clarendon Press
Oxford University Press (OUP) is the university press of the University of Oxford. It is the largest university press in the world, and its printing history dates back to the 1480s. Having been officially granted the legal right to print books ...
.
* Greenberg, Marvin Jay ''Euclidean and Non-Euclidean Geometries: Development and History'', 4th ed., New York: W. H. Freeman, 2007.
* Morris Kline (1972) ''Mathematical Thought from Ancient to Modern Times'', Chapter 36 Non-Euclidean Geometry, pp 861ŌĆō81, Oxford University Press
Oxford University Press (OUP) is the university press of the University of Oxford. It is the largest university press in the world, and its printing history dates back to the 1480s. Having been officially granted the legal right to print book ...
.
* Bernard H. Lavenda
Bernard Howard Lavenda (born September 18, 1945) is a retired professor of chemical physics at the University of Camerino and expert on irreversible thermodynamics. He has contributed to many areas of physics, including that of Brownian motion, a ...
, (2012) " A New Perspective on Relativity : An Odyssey In Non-Euclidean Geometries", World Scientific, pp. 696, .
* Nikolai Lobachevsky
Nikolai Ivanovich Lobachevsky ( rus, ąØąĖą║ąŠą╗ą░╠üą╣ ąśą▓ą░╠üąĮąŠą▓ąĖčć ąøąŠą▒ą░č湥╠üą▓čüą║ąĖą╣, p=n╩▓ik╔É╦łlaj ╔¬╦łvan╔Öv╩▓╔¬t╔Ģ l╔Öb╔É╦łt╔Ģ╔øfsk╩▓╔¬j, a=Ru-Nikolai_Ivanovich_Lobachevsky.ogg; ŌĆō ) was a Russian mathematician and geometer, k ...
(2010) ''Pangeometry'', Translator and Editor: A. Papadopoulos, Heritage of European Mathematics Series, Vol. 4, European Mathematical Society
The European Mathematical Society (EMS) is a European organization dedicated to the development of mathematics in Europe. Its members are different mathematical societies in Europe, academic institutions and individual mathematicians. The current ...
.
*
*
* Milnor, John W. (1982) Hyperbolic geometry: The first 150 years
', Bull. Amer. Math. Soc. (N.S.) Volume 6, Number 1, pp. 9ŌĆō24. * * * Stewart, Ian (2001) '' Flatterland'', New York: Perseus Publishing (softcover) * John Stillwell (1996) ''Sources of Hyperbolic Geometry'',
American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings ...
.
*
* A. Papadopoulos et Guillaume Th├®ret (2014) ''La th├®orie des parall├©les de Johann Heinrich Lambert'', (Critical edition of Lambert's memoir with a French translation, with historical and mathematical notes and commentaries ├®d. Blanchard, coll. Sciences dans l'Histoire, Paris
External links
* *Roberto Bonola (1912Non-Euclidean Geometry
Open Court, Chicago.
*
Non-Euclidean geometries
from ''Encyclopedia of Math'' of
European Mathematical Society
The European Mathematical Society (EMS) is a European organization dedicated to the development of mathematics in Europe. Its members are different mathematical societies in Europe, academic institutions and individual mathematicians. The current ...
and Springer Science+Business Media
Springer Science+Business Media, commonly known as Springer, is a German multinational publishing company of books, e-books and peer-reviewed journals in science, humanities, technical and medical (STM) publishing.
Originally founded in 1842 in ...
Synthetic Spacetime
a digest of the axioms used, and theorems proved, by Wilson and Lewis. Archived by WebCite. {{DEFAULTSORT:Non-Euclidean Geometry