Mixed Quantum-classical Dynamics

Mixed quantum-classical (MQC) dynamics is a class of computational theoretical chemistry methods tailored to simulate non- adiabatic (NA) processes in molecular and supramolecular chemistry. Such methods are characterized by:
# Propagation of nuclear dynamics through classical trajectories;
# Propagation of the electrons (or fast particles) through quantum methods;
# A feedback algorithm between the electronic and nuclear subsystems to recover nonadiabatic information.

Use of NA-MQC dynamics

In the Born-Oppenheimer approximation, the ensemble of electrons of a molecule or supramolecular system can have several discrete states. The potential energy of each of these electronic states depends on the position of the nuclei, forming multidimensional surfaces.

Under usual conditions (room temperature, for instance), the molecular system is in the ground electronic state (the electronic state of lowest energy). In this stationary situation, nuclei and electrons are in equilibrium, and the molecule naturally vibrates near harmonically due to the zero-point energy.

Particle collisions and photons with wavelengths in the range from visible to X-ray can promote the electrons to electronically excited states. Such events create a non-equilibrium between nuclei and electrons, which leads to an ultrafast response (picosecond scale) of the molecular system. During the ultrafast evolution, the nuclei may reach geometric configurations where the electronic states mix, allowing the system to transfer to another state spontaneously. These state transfers are nonadiabatic phenomena.

Nonadiabatic dynamics is the field of computational chemistry that simulates such ultrafast nonadiabatic response.

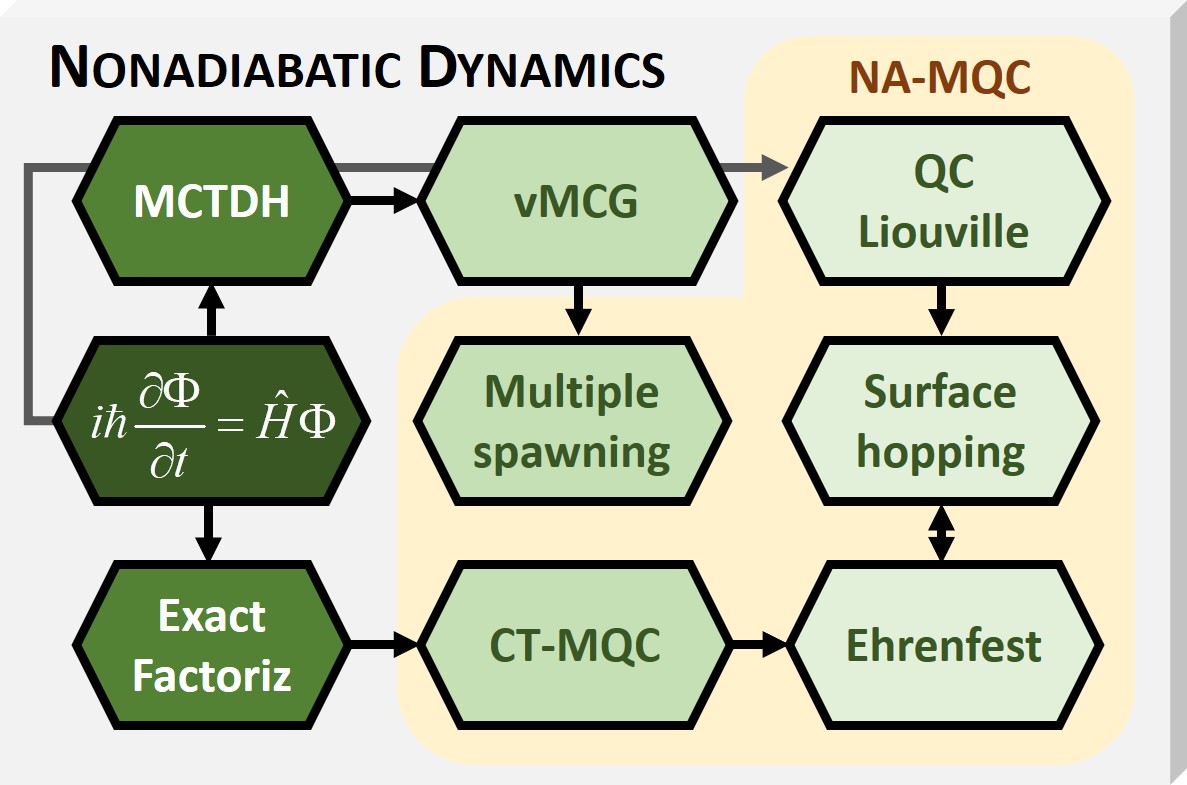
In principle, the problem can be exactly addressed by solving the time-dependent Schrödinger equation (TDSE) for all particles (nuclei and electrons). Methods like the multiconfigurational self-consistent Hartree (MCTDH) have been developed to do such task. Nevertheless, they are limited to small systems with two dozen degrees of freedom due to the enormous difficulties of developing multidimensional potential energy surfaces and the costs of the numerical integration of the quantum equations.

NA-MQC dynamics methods have been developed to reduce the burden of these simulations by profiting from the fact that the nuclear dynamics is near classical. Treating the nuclei classically allows simulating the molecular system in full dimensionality. The impact of the underlying assumptions depends on each particular NA-MQC method.

Most of NA-MQC dynamics methods have been developed to simulate internal conversion (IC), the nonadiabatic transfer between states of the same spin multiplicity. The methods have been extended, however, to deal with other types of processes like intersystem crossing (ISC; transfer between states of different multiplicities) and field-induced transfers.

NA-MQC dynamics has been often used in theoretical investigations of photochemistry and femtochemistry, especially when time-resolved processes are relevant.

List of NA-MQC dynamics methods

NA-MQC dynamics is a general class of methods developed since the 1970s. It encompasses:

# Trajectory surface hopping (TSH; FSSH for ''fewest switches surface hopping'');
# Mean-field Ehrenfest dynamics (MFE);
# Coherent Switching with Decay of Mixing (CSDM; MFE with Non-Markovian decoherence and stochastic pointer state switch);
# Multiple spawning (AIMS for ''ab initio multiple spawning''; FMS for ''full multiple spwaning'');
# Coupled-Trajectory Mixed Quantum-Classical Algorithm (CT-MQC);
# Mixed quantum−classical Liouville equation (QCLE);
# Mapping approach;
# Nonadiabatic Bohmian dynamics (NABDY);
# Multiple cloning; (AIMC for ''ab initio multiple cloning'')
# Global Flux Surface Hopping (GFSH);
# Decoherence Induced Surface Hopping (DISH)

Integration of NA-MQC dynamics

Classical trajectories

The classical trajectories can be integrated with conventional methods, as the Verlet algorithm. Such integration requires the forces acting on the nuclei. They are proportional to the gradient of the potential energy of the electronic states and can be efficiently computed with diverse electronic structure methods for excited states, like the multireference configuration interaction (MRCI) or the linear-response time-dependent density functional theory (TDDFT).

In NA-MQC methods like FSSH or MFE, the trajectories are independent of each other. In such a case, they can be separately integrated and only grouped afterward for the statistical analysis of the results. In methods like CT-MQC or diverse TSH variants, the trajectories are coupled and must be integrated simultaneously.

Electronic subsystem

In NA-MQC dynamics, the electrons are usually treated by a local approximation of the TDSE, i.e., they depend only on the electronic forces and couplings at the instantaneous position of the nuclei.

Nonadiabatic algorithms

There are three basic algorithms to recover nonadiabatic information in NA-MQC methods:

# Spawning - new trajectories are created at regions of large nonadiabatic coupling.
# Hopping - trajectories are propagated on a single potential energy surface (PES), but they are allowed to change surface near regions of large nonadiabatic couplings.
# Averaging - trajectories are propagated on a weighted average of potential energy surfaces. The weights are determined by the amount of nonadiabatic mixing.

Relation to other nonadiabatic methods

NA-MQC dynamics are approximated methods to solve the time-dependent Schrödinger equation for a molecular system. Methods like TSH, in particular in the fewest switches surface hopping (FSSH) formulation, do not have an exact limit. Other methods like MS or CT-MQC can in principle deliver the exact non-relativistic solution.

In the case of multiple spawning, it is hierarchically connected to MCTDH, while CT-MQC is connected to the exact factorization method.

Drawbacks in NA-MQC dynamics

The most common approach in NA-MQC dynamics is to compute the electronic properties on-the-fly, i.e., at each timestep of the trajectory integration. Such an approach has the advantage of not requiring pre-computed multidimensional potential energy surfaces. Nevertheless, th
costs associated with the on-the-fly approach
are significantly high, leading to a systematic level downgrade of the simulations. This downgrade has been shown to lead to qualitatively wrong results.

The local approximation implied by the classical trajectories in NA-MQC dynamics also leads to failing in the description of non-local quantum effects, as tunneling and quantum interference. Some methods like MFE and FSSH are also affected by decoherence errors. New algorithms have been developed to include tunneling and decoherence effects. Global quantum effects can also be considered by applying quantum forces between trajectories.

Software for NA-MQC dynamics

Survey of NA-MQC dynamics implementations in public software.

''^a'' Development version.

References

{{reflist

Computational chemistry