Milü

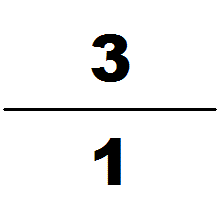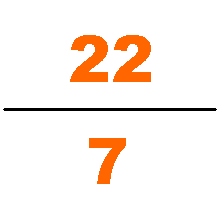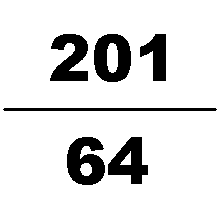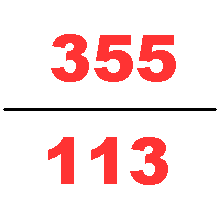''Milü'' (), also known as Zulü (Zu's ratio), is the name given to an approximation of ( pi) found by the Chinese mathematician and astronomer Zu Chongzhi during the 5th century. Using Liu Hui's algorithm, which is based on the areas of regular polygons approximating a circle, Zu computed as being between 3.1415926 and 3.1415927 and gave two rational approximations of , and , which were named ''yuelü'' () and ''milü'' respectively.

is the best rational approximation of with a denominator of four digits or fewer, being accurate to six decimal places. It is within % of the value of , or in terms of common fractions overestimates by less than . The next rational number (ordered by size of denominator) that is a better rational approximation of is , though it is still only correct to six decimal places. To be accurate to seven decimal places, one needs to go as far as . For eight, is needed.

The accuracy of ''milü'' to the true value of can be explained using the continued fraction expansion of , the first few terms of which are . A property of continued fractions is that truncating the expansion of a given number at any point will give the best rational approximation of the number. To obtain ''milü'', truncate the continued fraction expansion of immediately before the term 292; that is, is approximated by the finite continued fraction , which is equivalent to ''milü''. Since 292 is an unusually large term in a continued fraction expansion (corresponding to the next truncation introducing only a very small term, , to the overall fraction), this convergent will be especially close to the true value of :

:$\pi = 3 + \cfrac \quad\approx\quad 3 + \cfrac = \frac$

Zu's contemporary calendarist and mathematician He Chengtian invented a fraction interpolation method called 'harmonization of the divisor of the day' () to increase the accuracy of approximations of by iteratively adding the numerators and denominators of fractions. Zu's approximation of  ≈  can be obtained with He Chengtian's method.

See also

* Continued fraction expansion of and its convergents
*Approximations of π
*Pi Approximation Day

Notes

References

External links

Fractional Approximations of Pi

{{DEFAULTSORT:Milu
Pi
History of mathematics
History of science and technology in China
Chinese mathematical discoveries
Chinese words and phrases
Approximations
Rational numbers
Zu Chongzhi